二、物体是由分子组成的

物体是由分子组成的，这在化学中已经学过了。这一节讲讲分子的大小和阿伏伽德罗常数。

分子的大小  分子看不见，摸不到，怎样能知道分子的大小呢？

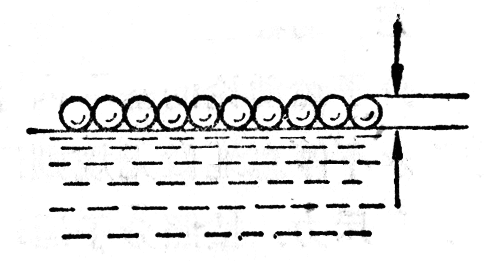
一种粗略地测定分子大小的方法是油膜法：把油滴滴到水面上，油在水面上要尽可能地散开，形成单分子油膜（图1-1）。如果把分子看成球形，单分子油膜的厚度就可以认为等于油分子的直径。事先测出油滴的体积，再测出油滴在水面上散开的面积，就可以算出单分子油膜的厚度，这样就测出了分子的直径。测定结果表明，分子直径的数量级是10^-10m。

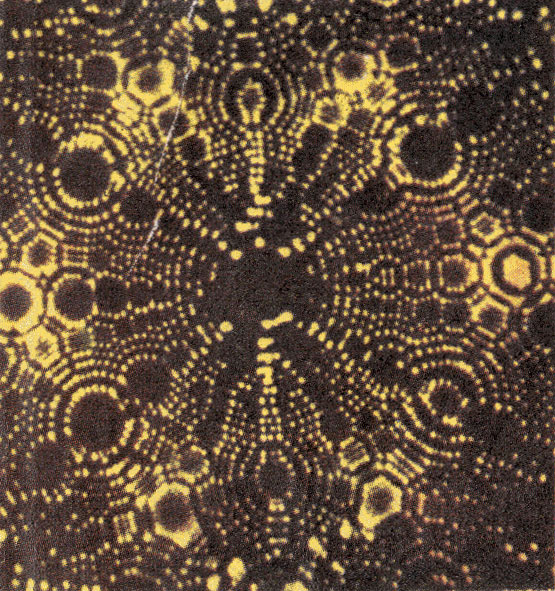
现在有了能放大上百万倍的离子显微镜，用它可以看到钨针针尖上原子分布的图样（见插页彩图1），并且可以测出钨原子间的距离大约是2×10^-10m。设想钨原子是一个挨着一个排列的，那么，可以认为钨原子间的距离2×10^-10m就是钨原子的直径。

物理学中有各种不同的方法来测定分子的大小。用不同方法测出的分子的大小并不完全相同，但是数量级是相符的。测定的结果表明，一般分子直径的数量级是10^-10m。例如水分子的直径是4.0×10^-10m，氢分子的直径是2.3×10^-10m。

需要指出的是：把分子看作小球，是分子运动论中对分子的简化模型；实际上，分子有它复杂的内部结构，并不真是小球。因此，说分子的直径有多大，一般知道数量级已经可以了，它提供了关于分子大小的一个数量观念，使我们了解分子是多么微小。

阿伏伽德罗常数  我们在化学课中学过，1摩尔（摩尔简称摩，国际符号是mol。）的任何物质，其中含有的粒子数相同，都等于12克碳-12中含有的原子数。这个数叫做阿伏伽德罗常数。

知道分子的大小，可以粗略地算出阿伏伽德罗常数，例如1摩的水，质量是1.8×10^-2千克，体积是1.8×10^-5米³。水分子的直径是4.0×10^-10米，体积大约是3×10^-29米³。设想水分子是一个挨一个排列的，我们可以算出1摩的水中所含的分子数：

N＝\(\frac{{1.8 \times {{10}^{{\rm{ - }}5}}{{\rm{m}}^{\rm{3}}}{\rm{/mol}}}}{{3 \times {{10}^{ - 29}}{{\rm{m}}^{\rm{3}}}}}\)＝6.02×10²³mol^-1。

早期测定阿伏伽德罗常数的一种方法，就是利用油膜法测出分子直径，得出这个常数的。这种测定方法比较粗略，但得出的数量级是正确的。

我们看到，阿伏伽德罗常数是一个十分巨大的数字，为了说明这个数字有多么大；我们设想有一个极小的动物来喝水，它每秒钟喝进100亿个分子，要二百万年才能把1摩的水喝完。

反过来，知道了阿伏伽德罗常数，对液体和固体很容易估算分子的大小。知道液体和固体的摩尔体积，设想其中的分子是一个挨一个排列的，利用阿伏伽德罗常数就可以算出一个分子所占的体积，从而估算出它的直径。

知道了阿伏伽德罗常数，还可以算出分子的质量。水的摩尔质量是1.8×10^-2千克/摩，1摩的水中含有6×10²³个分子，所以一个水分子的质量是

m_H2O＝\(\frac{{1.8 \times {{10}^{{\rm{ - 2}}}}}}{{6 \times {{10}^{23}}}}\)kg＝3×10^-29kg。

可见水分子的质量是很小的，除了包含几千个原子的有机物大分子外，一般分子的质量也是这个数量级。

反过来，知道分子的质量，也可以算出阿伏伽德罗常数。物理中有办法测出分子的质量，例如精确测得一个碳原子的质量是1.995×10^-26千克，由此不难得出阿伏伽德罗常数。

阿伏伽德罗常数是微观世界的一个重要常数，用分子运动论定量地研究热现象经常要用到它，它是联系微观世界和宏观世界的桥梁。从上面所讲的我们可以看出，阿伏伽德罗常数把摩尔质量或摩尔体积这种宏观物理量跟分子质量或分子大小这种微观物理量联系起来了。

正因为阿伏伽德罗常数这样重要，所以物理学家们想出各种办法来测定它，一百多年以来不断努力来更精确地测定它。后面我们讲到电学的时候，就要提到一种测定阿伏伽德罗常数的方法。现在测得的阿伏伽德罗常数的精确值是

N＝6.022045×10²³摩^-1。

通常可取作                                N＝6.02×10²³摩^-1。

阅读材料：离子显微镜

课文中提到，用离子显微镜可以测出钨原子的直径。现在简单介绍一下离子显微镜的构造和原理。

离子显微镜由半径约为10厘米的球形玻璃容器和一根钨针组成，钨针的针尖放在容器的中心（图1-2）。针尖的表面可以看作是半径非常小的球面，近代金属加工技术可以做到使这个半径约为5×10^-6厘米。在球形容器的内表面涂上一薄层导电物质，象电视荧光屏那样，在快速粒子打击下可以发光。在导电层和针尖之间加上高电压，使导电层带负电，针尖带正电。

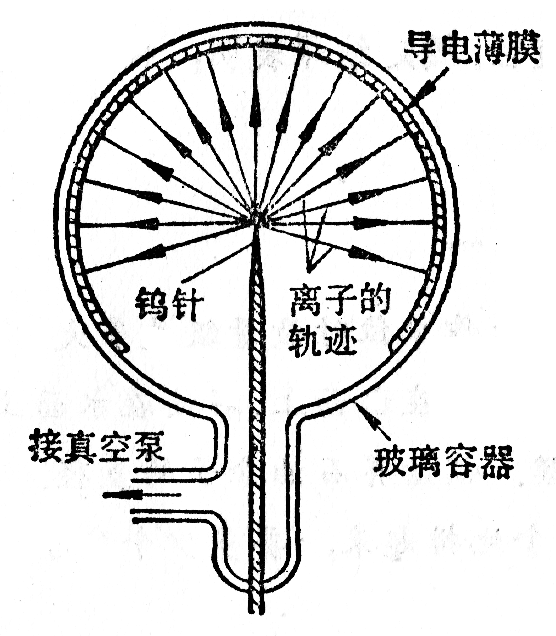
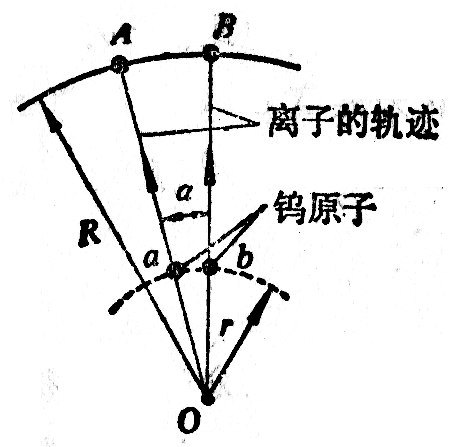
在球形容器中充满低压的氦气。当无规则运动的氦原子与针尖上的钨原子碰撞时，由于氦原子失去电子成为正离子，氦离子在电力作用下就离开针尖，以很大速度沿着球半径运动，打到球形容器的内表面上使之发光，这样，就出现了钨针针尖上原子分布的图样（图1-3）。

图1-3中弧长ab表示相邻两个钨原子间的距离，弧长AB表示它们在球形容器内表面上的像之间的距离。因为AB＝Rα，ab＝rα，所以放大倍数K＝\(\frac{{AB}}{{ab}} = \frac{R}{r}\)＝2×10⁶，即放大二百万倍，已知放大倍数，测出弧长AB，就可以求出原子间的距离ab。设想钨原子是一个挨一个排列的，可以认为距离ab等于钨原子的直径，测定结果表明，钨原子的直径是2×10^-10米。

练习一

（1）一般分子的直径，以厘米作单位时数量级是多大？

（2）把体积为1mm³的石油滴在水面上，石油在水面上形成面积为3m²的单分子油膜，试估算石油分子的直径。

（3）设想把分子一个挨一个地排起来，要多少个分子才能排满1米的长度？

（4）1cm³水中含有多少个水分子？10g氧中含有多少个氧分子？

（5）一个氧分子、一个氢分子的质量各是多少千克？

（6）已经测得一个碳原子的质量是1.995×10^-20kg，求阿伏伽德罗常数。

（7）已知金刚石的密度是3500kg/m³。有一小块金刚石，体积是5.7×10^-8m³。这小块金刚石中含有多少个碳原子？设想金刚石中碳原子是紧密地堆在一起的，估算碳原子的直径。

发布时间：2015/8/16 下午12:39:41  阅读次数：3278