六、简谐振动的能量
现在从能量的角度来看一看简谐振动,简谐振动不考虑阻力,振动系统的机械能是守恒的。
以单摆为例,当我们把摆锤从平衡位置O拉到B点时(图9-3),摆锤的位置升高,我们克服重力做了功,做功消耗的能转化为摆锤的重力势能,储存在这个振动系统之中。
把拉到B点的摆锤放开后,在回复力作用下,摆锤向左做变加速运动,位置降低,速度增大,重力势能转化为动能。当回到平衡位置O时,重力势能减少到零(取平衡位置时的重力势能为零),动能达到最大值,而且这时的动能就等于摆锤在最大位移时的重力势能。
当摆锤越过平衡位置O向着C点做变减速运动的过程中,位置升高,速度减小,动能转化为重力势能。当摆锤运动到C点时,动能减少到零,重力势能达到最大值,而且等于最初储存在系统中的重力势能。
此后,摆锤又向平衡位置运动,重力势能又转化为动能;过了平衡位置继续向B点运动,动能又转化为重力势能。这种转化重复不息,一直进行下去,而摆锤在任何位置(或任何时刻)的机械能即动能和重力势能之和保持不变,都等于最大位移处的重力势能。我们最初把摆锤拉到B点,摆锤在B点的位移越大,位置越高,储存在振动系统中的重力势能越大。可见简谐振动的能量跟振幅有关:振幅越大,简谐振动的能量就越大。
在图9-2所示的弹簧振子里也进行着相似的能量转化过程,只不过跟动能相互转化的不是重力势能而是弹性势能。当我们把弹簧振子从平衡位置拉到B点时,克服弹簧的弹力做了功,做功消耗的能转化为弹性势能储存在振动系统之中。把振子放开,在振动过程中弹性势能和动能相互转化,而且重复不息,一直进行下去。弹簧振子在任何位置(或任何时刻)的机械能即动能和弹性势能之和保持不变,都等于最大位移处的弹性势能。我们知道,弹簧的弹性势能跟弹簧被拉伸或压缩的长度有关系,这个长度越大,弹性势能也越大。可见,振子在B点的位移越大,储存的弹性势能就越大。在弹簧振子中我们同样看到:振幅越大,简谐振动的能量就越大。
简谐振动是一种理想化的振动,一旦供给振动系统一定的能量来使它开始振动,由于机械能守恒,它就要以一定的振幅永不停息地振动下去。可是实际上振动系统不可避免地要受到摩擦和其他阻力,即受到阻尼的作用。振动系统克服阻尼作用做功,系统的机械能就要损耗。这样,机械能随着时间逐渐减少,振动的振幅也逐渐减小。待到机械能耗尽之时,振动就停下来了。这种振幅逐渐减小的振动叫做阻尼振动。图9 -11是阻尼振动的图象。
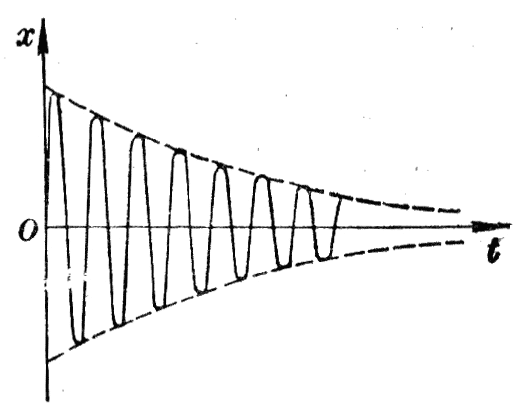
振动系统受到的阻尼越大,振幅减小得越快,振动停下来也越快。阻尼过大将不能产生振动。阻尼越小,振幅减小得越慢。在阻尼很小时,在一段不太长的时间内看不出振幅有明显的减小,就可以把振动系统当作简谐振动来处理。前面关于简谐振动的演示就属于这种情形。
练习五
分析弹簧振子(图9-2)和单摆(图9-3)在振动中能量的转化情况,填好下表:
| 振子的运动 | C→O | O→B | B→O | O→C |
| 能量的变化(增多或减少) | 动能 | |||
| 势能 | ||||
| 总能 |
发布时间:2015/8/14 下午6:51:00 阅读次数:7611
