二、简谐振动

振动现象是很普遍的，是多种多样的，我们怎样着手研究它呢？小鸟从树枝上飞开，树枝就振动起来。这个现象看来比较简单，可是真要研究它，所要考虑的因素却很复杂，不便于我们着手研究，跟研究其他现象一样，研究振动现象也要从最简单、最基本的振动来着手。前一节我们说过，产生振动的第一个必要条件是要有回复力的作用，回复力的性质是各种各样的，我们希望着手被研究的那种振动，所受的回复力要比较简单。假如回复力是弹簧的弹力，我们希望弹簧的形变在弹性限度之内，因为这时弹力跟形变成正比。产生振动的第二个必要条件是阻力足够小。既然如此，我们着手研究的时候，暂时就不去考虑阻力，而研究一种无阻力的理想化的振动。这就是这一节要讲的简谐振动。

这里我们再一次遇到所谓理想化的方法。这是研究物理现象经常采用的方法，这样做的好处是使复杂问题变得简单，便于人们就这种简单情况深入探讨，然后再把暂时被抛开的因素和其他因素考虑进去，逐步由简单到复杂。简谐振动不但是研究复杂振动的基础，它本身也具有实际意义，许多复杂的振动在振幅小的情况下可以近似地看作是简谐振动。一切复杂的振动都可以看作是若干振幅、频率不同的简谐振动合成的。

简谐振动的特点是什么呢？下面我们通过一个典型例子来说明，这个典型例子就是弹簧振子。

弹簧振子      照图9-2那样，把连在一起的弹簧和小球穿在水平杆上，弹簧左端固定在支架上，小球可以在杆上滑动。杆非常光滑，小球滑动时的摩擦力可以忽略，掸簧的质量比小球的小得多，也可以忽略，这样就成了一个弹簧振子。振子静止在O点时，它受的重力和杆的支持力互相平衡，弹簧没有形变因而对它没有弹力作用，O点就是振子的平衡位置。把它拉离平衡位置再放开，它就沿水平杆左右振动。

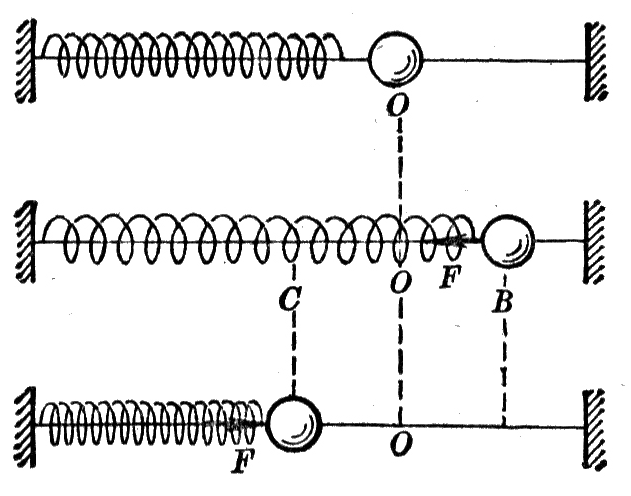
在振子振动过程中，重力和杆的支持力总是互相平衡，对振动不起作用，对振动起作用的只是弹簧作用在振子上的弹力。振子运动到O点右侧时，弹簧拉长，振子对平衡位置的位移方向向右，弹簧对振子的弹力方向向左。振子运动到O点左侧时，弹簧压缩，振子对平衡位置的位移方向向左，弹簧对振子的弹力方向向右。可见在这个弹簧振子上，总是指向平衡位置的回复力是弹簧对振子的弹力。这个弹力的方向跟振子对平衡位置的位移方向相反。

根据胡克定律，在振幅不大（弹簧不超出弹性限度）的情况下，弹簧振子回复力F的大小跟弹簧伸长或缩短的长度x成正比，而这个长度就是振子对平衡位置的位移的大小，因此回复力F的大小跟这个位移x的大小成正比。刚刚讲过，回复力的方向跟这个位移的方向相反。这样，用下式就可以把回复力的大小和方向都表示出来：

F＝－kx。

式中k是比例常数，对于弹簧振子来说，就等于弹簧的倔强系数。式中的负号表示回复力的方向跟位移的方向相反。

这种在跟对平衡位置的位移成正比而方向相反的回复力作用下的振动，叫做简谐振动。

用m代表振子的质量，用a代表振子的加速度，根据牛顿第二定律F＝ma可以得到

\[a = - \frac{k}{m}x\]

上式表明，在简谐振动中，加速度也跟位移成正比而方向相反。在图9-2里，当振子从O向右运动时，加速度的方向向左，并且随着位移增大而增大，即振子做变减速运动。到速度减小到零时，振子运动到右端最大位移处B，加速度也增大到最大值。振子从B向O运动的过程中，加速度的方向仍向左，并且随位移的减小而减小，即振子做初速度为零的变加速运动。当振子回到O点时，位移减小到零，加速度也减小到零，而速度增大到最大值，方向向左。由于惯性，振子就以这个速度继续向左运动。在越过O点以后，加速度的方向向右，并且随位移的增大而增大，振子做变减速运动。到速度减小到零时，振子运动到左端最大位移处C，加速度也增大到最大值。然后振子从C向右运动，加速度的方向仍向右，并且随位移的减小而减小，即振子做初速度为零的变加速运动。当振子回到O点时，位移、加速度都减小到零，而逮度增大到最大值，方向向右。此后将重复上述的过程。

值得注意的是，在简谐振动中速度与加速度的变化不一样，加速度最大时速度等于零，加速度等于零时速度最大。

简谐振动的周期  简谐振动的周期跟什么有关呢？在回复力的表示式F＝－kx中，k越大，回复力越大，振子产生的加速度越大，振子来回振动得越快，因而周期越短。在图9-2中用不同倔强系数的弹簧做实验，可以看到倔强系数越大，振子的周期越短。其次，振子的质量m越大，产生的加速度越小，振子来回振动得越慢，因而周期越长。在图9-2中用不同质量的振子做实验，可以看到质量越大，振子的周期越长。

计算表明，弹簧振子的周期由下式确定：

\[T = 2\pi \sqrt {\frac{m}{k}} \]

可见，弹簧振子的周期跟质量的平方根成正比，跟弹簧的倔强系数的平方根成反比，而跟振幅无关。

上式对其他简谐振动也适用，只是对其他简谐振动，k的含义不同了。下一节讲到单摆就可以看出这一点。因此上式就是简谐振动的周期公式。

由周期公式知道，对于一个确定的简谐振动系统来说，m和k都是恒量，所以T也是恒量，只由系统本身的特性决定，叫做系统的固有周期。因为f＝1/T，所以f也只由系统本身的特性决定，叫做系统的固有频率，值得注意的是固有周期和固有频率都跟振幅没有关系。

练习二

（1）物体在任意回复力作用下振动，一定是做简谐振动吗？为什么？

（2）用手拍球，使球在硬地上来回跳动，球的运动是简谐振动吗？为什么？

（3）分析图9-2中弹簧振子的运动，并填好下表：

（4）图9-2所示的弹簧振子的质量是100g，频率为2Hz，求弹簧的倔强系数。

（5）一个如图9-2所示的弹簧振子的质量是200g，弹簧的倔强系数是16N/m。振幅是2cm，取水平向右的方向作为正方向。当振子运动到右方最大位移时，回复力和加速度的数值各是多大？当振子运动到左方最大位移时，回复力和加速度的数值又各是多大？这个弹簧振子的周期和频率备是多大？

发布时间：2015/8/12 下午4:10:43  阅读次数：1253