七、反冲运动

打炮的时候，炮弹从炮筒中飞出，炮身就向后退，这个现象可以用动量守恒定律来说明。射击前，炮弹静止在炮筒里，它们的总动量为零。炮弹射出后以很大的速度向前运动，炮弹具有了动量，但是根据动量守恒定律，炮弹和炮筒的动量之和还应该等于零，因此炮身得到与炮弹的动量大小相等、方向相反的动量。只是由于炮身的质量比炮弹的大得多，所以炮身向后运动的速度很小。炮身的这种后退运动叫做反冲运动。炮身的反冲运动是不利的，为了使大炮回到原来的位置并重新瞄准，要花不少时间，这就降低了射击速度。现代的大炮都安装了使大炮在发射后自动迅速复位的装置。此外，人们还发明了无后座力炮，这种炮在发射时火药气从炮身后面的开口喷出，炮身不受火药气的向后的压力，因此发射时不后退。

反冲运动在科学技术中也有许多重要的应用，喷气式飞机、火箭就是利用反冲运动来获得巨大速度的。喷气式飞机通过连续不断地向后喷出气体，可以得到超过音速的飞行速度。

我国早在宋代就发明了火箭，古代火箭的构造跟现在节日里玩的“起花”相似。茌竹筒里装入一些火药，把竹筒捆在箭杆上，火药点燃后，燃烧生成的气体以很大的速度从筒里向后喷出，竹筒带着箭就向前飞去（图8-8）。这种火箭在古代曾作兵器用过。

现代火箭的原理跟上面的基本相同，只是构造比较复杂。它主要由壳体和燃料两大部分组成，壳体是圆筒形的，前端是封闭的尖顶，后端有尾喷管，燃料燃烧时产生的高温高压气体以很大的速度从尾部向后喷出，火箭就向前飞去（图8-9）。

理论计算表明，火箭获得的最终速度主要取决于两个条件，一个是喷气速度，一个是质量比，即火箭开始飞行时的质量与燃料燃尽时的质量之比。为了提高喷气速度，需要使用高质量的燃料，目前常用的液体燃料是液氢，用液氧做氧化剂，质量比与火箭的结构和材料有关系，现代技术能达到的质量比不超过10。在现代技术条件下，用一级火箭还不能达到发射人造卫星所需要的速度。要发射人造卫星，现在都用多级火箭。

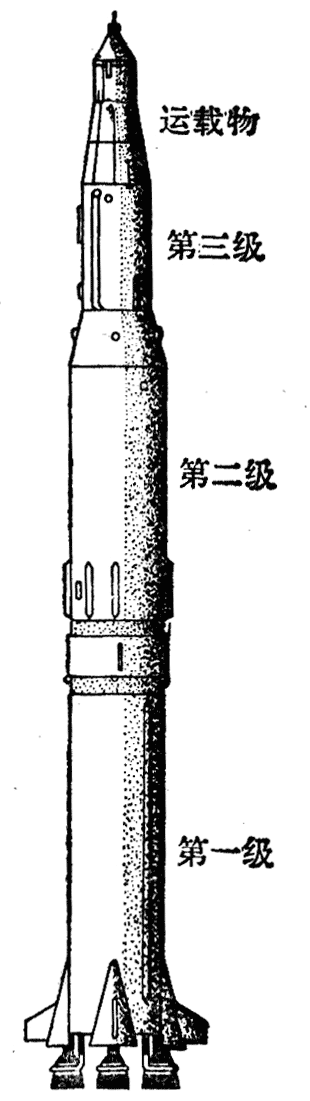
多级火箭是由单级火箭组成的（图8-10）。发射时先点燃第一级火箭，它的燃料用完以后空壳就自动脱离，这时第二级火箭开始工作。第二级火箭在燃料用完以后空壳也自动脱离，以后又是下一级火箭开始工作，多级火箭在工作中及时把对后面航行没有用的空壳抛掉，使火箭的总质量减少，因此能够达到很高的速度，可以用来发射人造卫星、宇宙飞船和洲际导弹。当然，火箭的级数也不是越多越好，因为级数越多，火箭的构造也越复杂，工作的可靠性也越差。目前，多级火箭一般都是三级的。

现代的火箭，工作时推力的大小很不一样。小的如空对空导弹的火箭，推力只有几万牛，大的如发射人造卫星的火箭和洲际导弹的火箭，推力可达几百万牛以上。

火箭技术与科学技术和国防的现代化都有很大的关系，是现代的一门重要尖端技术。我国已经运用自己研制的火箭多次发射过人造卫星和远程导弹。我们还要进一步提高火箭技术，尽快地赶上和超过国外的先进水平。我们相信，在同学们中，一定会有人在这一重要领域内为祖国作出卓越的贡献！

复习题

（1）什么是冲量？什么是动量？冲量一定时，作用力的大小与力的作用时间有什么关系？动量一定时，物体的质量与运动速度之间有什么关系？

（2）什么是动量定理？

（3）什么是动量守恒定律？

（4）什么叫弹性碰撞？什么叫非弹性碰撞？什么叫完全非弹性碰撞？哪种碰撞动能的损失最大？

习题

（1）质量为1kg的手榴弹以60°角斜抛出去，抛出的速度为10m/s，手榴弹到达最高点时炸成两块，一块的质量是0.6kg，以15m/s的速度沿原方向运动，求另一块的速度大小和方向。

（2）对于在一直线上运动的两个物体组成的系统，动量守恒定律的一般表达式为：

m₁v₁＋m₂v₂＝m₁v₁ʹ＋m₂v₂ʹ。

在不同情况下，这个表达式往往可以简化为不同形式，试写出下列各种情况下得出的简化的表达式：

①两个物体原来静止，发生相互作用后分开；

②一个物体原来静止，另一个物体跟它碰撞后粘合在一起并共同沿原来的方向运动；

③一个物体原来静止，另一个运动物体与它正碰后，两物体以不同的速度在原来的直线上运动；

④两个相向运动的物体，相碰后都静止下来。

（3）试证明：两个物体碰撞后，它们的速度变化Δv₁＝v₁ʹ－v₁和Δv₂＝v₂ʹ－v₁跟它们的质量成反比。即

\[\frac{{\Delta {v_1}}}{{\Delta {v_2}}} = - \frac{{{m_2}}}{{{m_1}}}\]

并利用所得结果来讨论：很轻的物体（如乒乓球）跟一个根重的物体（如课桌）碰撞后，它们的速度变化有什么特征。

（4）质子的质量是1.67×10^-27kg，速度为1.0×10⁷m/s，与一个静止的氦核碰撞后，质予以6.0×10⁶m/s的速度反弹回来，氦核以4.0×10⁶m/s的速度向前运动。

①你能否求出氦核的质量？如果能，是多少？

②你能否求出碰撞时的相互作用力？为什么？

（5）两个球以相同的速度相向运动，其中一个球的质量是另一个的三倍。相碰后重球停止不动，轻球以二倍的速率弹回，试证明它们发生的是弹性碰撞。

（6）在光滑水平面上一个质量为0.2kg的小球以5m/s的速度向前运动，途中与另一个质量为0.3kg静止的小球发生正碰，假设碰撞后第二个小球的速度为4.2m/s，你算出的第一个小球的速度是多大？想一想，这种情况真的可能发生吗？这道题的毛病出在哪里？

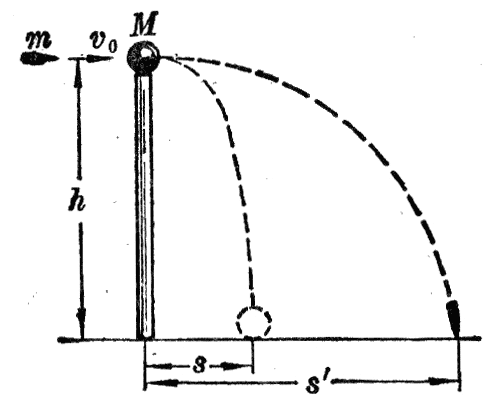
（7）一个质量M＝0.2kg的小球放在高度h＝5m的直杆顶端（图8-11）。一颗质量m＝0.01kg的子弹以v₀＝500m/s的速度沿水平方向击中小球，并穿过球心，小球落地处离杆的距离s＝20m。求子弹落地处离杆的距离。子弹的动能有多少转化成了热能？

（8）一个连同装备共有100kg的宇宙航行员，脱离宇宙飞船后，在离飞船45m处与飞船处于相对静止状态。他带着一个装有0.5kg氧气的贮氨筒，贮氧筒有个可以使氧气以50m/s的速度喷出的喷嘴，宇航员必须向着与返回飞船相反的方向释放氧气，才能回到飞船上去，同时又必须保留一部分氧气供他在飞回飞船的途中呼吸。飞行员呼吸的耗氧率为2.5×10^-4kg/s。如果他在开始返回的瞬间释放0.1kg的氧气，他能安全回到飞船吗？

解：宇航员向着与返回飞船相反的方向释放出m＝0.1kg的氧气后，他将获得向着飞船运动的速度，要知道宇航员能否安全回到飞船，先要求出它返回飞船需要的时问t。取飞船为参照物，向着飞船运动的方向为正方向，氧气释放的速度v＝－50m/s。设宇航员获得的速度为V，宇航员连同装备的总质量为M。原来宇航员相对于飞船是静止的，根据动量守恒定律可得：（M－m）V＋mv＝0。考虑到M≫m，得MV＋mv＝0，所以V＝－\(\frac{{mv}}{M}\)。设宇航员离飞船的距离为d，他返回飞船所需的时间

\[t = \frac{d}{V} = - \frac{{Md}}{{mv}} = - \frac{{100 \times 45}}{{0.1 \times ( - 50)}}{\rm{s}} = 900{\rm{s}}\]

宇航员呼吸的耗氧率R＝2.5×10^-4kg/s，在返回飞船这段时间t内他呼吸需要的氧气

m_吸＝Rt＝2.5×10^-4×900kg＝0.23kg。

他释放0.1kg的氧气后，筒内剩余的氧气是

m_余＝（0.5－0.1）kg＝0.4kg。

由于他剩余的氧气多于他返回途中呼吸所需的氧气，因此他可以安全返回飞船。

（9）在上题中，如果宇航员想以最短的时间返回飞船，他开始最多能释放出多少氧气？这时他返回飞船所用的时间是多少？

（10）速度为10⁶cm/s的氦核与静止的质子发生正碰，氦核的质量是质子的4倍，碰撞是弹性的，求碰撞后两个粒子的速度。

（11）一个质量是m₁、动能是E_k的物体与一个质量是m₂的不动的物体正碰。假定发生的是弹性碰撞，在m₁＝0.01m₂，m₁＝m₂，m₁＝100m₂的情况下，m₁传递给m₂的动能各是多少？

（有兴趣的同学还可以进一步讨论m₁传递给m₂的动能最大或最小的条件）。

（12）在有些原子反应堆里，要让中子原子核碰撞，以便把中子的速率迅速降低下来，为此，是选用较重的还是较轻的原子核效果较好？为什么？

发布时间：2015/8/11 下午8:58:42  阅读次数：1921