十、机械能守恒定律的应用

机械能守恒定律广泛用来解决各种力学问题，下面通过例题来说明它的应用。

【例题1】竖直上抛的物体，初速度是 v₀，求物体上升的最大高度，不计空气阻力。

这个问题我们在第二章已经研究过，现在用机械能守恒定律来处理，竖直上抛的物体只受重力的作用，因而机械能守恒。

物体抛出时，动能是 \(\frac{1}{2}\)mv₀²，重力势能为零，机械能 E₁＝\(\frac{1}{2}\)mv₀²。物体达到最大高度H时，动能为零，重力势能是mgH，机械能 E₂＝mgH。因为E₁＝E₂，所以

mgH＝\(\frac{1}{2}\)mv₀²，

H＝\(\frac{{v_0^2}}{{2g}}\)

我们看到，用机械能守恒定律求得的答案跟我们在第二章用运动学的方法求得的结果完全相同。

用机械能守恒定律不但能处理直线运动问题，而且能处理曲线运动问题。直接应用牛顿第二定律和运动学的知识来处理力学问题特别是曲线运动，固然可以确定运动物体在任一时刻的位置和速度，从而获得关于这个力学问题的全面知识，但往往需要用高等数学来计算，有的计算还相当复杂。用机械能守恒定律来处理，却可以相当简便。

【例题2】一个摆长是 l 的单摆，最大偏角是 θ，求单摆在最低位置的速度（图 7-22）。

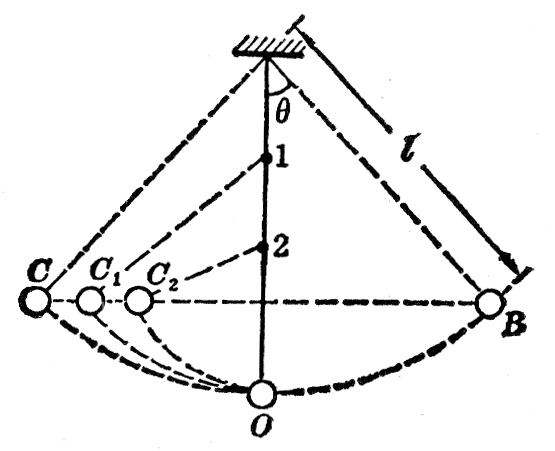
这个问题直接用牛顿第二定律和运动学的知识来处理，就需要用高等数学。现在用机械能守恒定律来处理。

摆锤受到两个力：重力和悬线的拉力。悬线的拉力始终垂直于摆锤的运动方向，不做功，所以单摆的机械能守恒。

选择摆锤在最低点时所在的水平面作参考平面，摆锤在最高点时，动能为零，重力势能是mg（l－lcosθ），机械能E₁＝mg（l－lcosθ）。摆锤在最低点时，动能是\(\frac{1}{2}\)mv²，重力势能为零，机械能E₂＝\(\frac{1}{2}\)mv²。因为E₁＝E₂，所以

\(\frac{1}{2}\)mv²＝mg（l－lcosθ），

v＝\(\sqrt {2gl(1 - \cos \theta )} \)。

我们看到，由于机械能守恒定律只涉及开始状态和终了状态的机械能，不涉及中间运动过程的细节，因此用它来处理问题相当简便。

当然，有的问题只用机械能守恒定律还不能完全解决，例如要想求单摆在最低位置时悬线的拉力F，就还需要应用圆周运动的知识，应用机械能守恒定律求出速度 v 之后，我们不难求出悬线的拉力：

F＝mg＋\(\frac{{m{v^2}}}{l}\)＝mg＋2mg（1－cosθ）。

解决力学问题，先从能量的观点入手分析，往往带来方便。应用机械能守恒定律来解决力学问题，也要先分析物体的受力情况。在动能和重力势能的相互转化中，如果只有重力做功，其他力不做功，就可以应用机械能守恒定律。

守恒定律不仅给处理问题带来方便，而且有更深刻的意义。物理世界是千变万化的，但是人们发现有些物理量在一定条件下是守恒的，可以用这些“守恒量”来表示物理世界变化的规律，这就是守恒定律。机械能守恒定律就是其中一个，正因为自然界存在着“守恒量”，而且某些守恒定律的适用范围很广泛，所以在物理学中寻求“守恒量”已经成为物理研究工作的一个重要方面，下一章我们将学习另一个守恒定律——动量守恒定律。

练习七

（1）滑雪运动员从25m高的山坡上滑下，如果阻力忽略不计，他滑到坡底叶的速度是多大？

（2）物体从高H的光滑斜面的顶端滑下，证明物体到达斜面末端时的速度v＝\(\sqrt {2gH} \)。

（3）蒸汽打桩机的重锤的质量是250kg，把它提升到离地面25m高处，然后让它自由落下，计算：①重锤在最高点的动能、重力势能和机械能。②重锤下落10m时的重力势能、动能和速度。③重锤落到地面时的重力势能、动能和速度。

（4）要使一球着地后回跳的高度超过原高10m，必须以多大速度将它下抛？不计球击地时的能量损失。

（5）一个物体从距地面40m的高处自由落下，经过几秒后，该物体的动能和重力势能相等？g＝10m/s²。

发布时间：2015/7/31 下午2:02:51  阅读次数：1367