九、机械能守恒定律

机械能的相互转化   动能和势能（重力势能和弹性势能）统称为机械能，一种形式的机械能是可以和另一种形式的机械能相互转化的。下面我们看一些例子。

物体自由下落或者沿着光滑斜面滑下的时候，重力对物体做功，物体的重力势能减少。而物体的速度越来越大，表示物体的动能增加了，这时重力势能转化成动能。

原来具有一定速度的物体，在竖直上升或者沿着光滑斜面上升的时候，物体克服重力做功，速度越来越小，物体的动能减少了，同时物体的高度增加，重力势能增加了。这时动能转化成重力势能。

弹性势能也可以跟动能相互转化。放开一个被压缩的弹簧，它可以把一个跟它接触的小球弹出去，这时弹力做功，弹簧的弹性势能减少，同时小球得到一定的速度，动能增加，放开被拉开的弓把箭射出去，这时弓的弹性势能减少，箭的动能增加。

从这些例子我们看到，机械能的相互转化是通过重力或弹力做功来实现的。重力或弹力做功的过程，也就是机械能从一种形式转化成另一种形式的过程，下面我们进一步来研究重力或弹力做功的多少跟这种转化的定量关系。

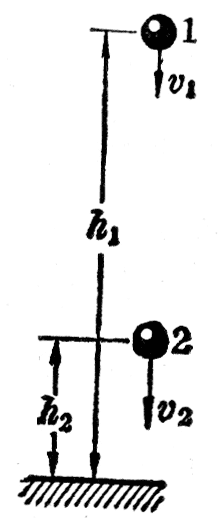
机械能的守恒      我们先用自由落体作例子定量的研究动能和重力势能的转化（图7-20）。设有一个质量是m的物体，从高度是h₁的地方（起点）下落到高度是h₂的地方（终点）。设物体在起点的速度为v₁，在终点的速度为v₂。物体在下落过程中，重力做了功。从动能定理知道，重力所做的功等于物体动能的增加，即

W_G＝\(\frac{1}{2}\)mv₂²－\(\frac{1}{2}\)mv₁²。

另一方面，从重力做功与重力势能的关系知道，重力所做的功等于重力势能的减少，即

W_G＝mgh₁－mgh₂。

这样，我们得到

\(\frac{1}{2}\)mv₂²－\(\frac{1}{2}\)mv₁²＝mgh₁－mgh₂。

这就是说，重力做了多少功，就有多少重力势能转化成等量的动能。把上式移项后得到

\(\frac{1}{2}\)mv₂²＋mgh₂＝\(\frac{1}{2}\)mv₁²＋mgh₁。

上式表示，物体在自由下落中，它的重力势能转化成动能，但在任何时刻，动能和重力势能之和亦即它的机械能保持不变。

上述结论不仅对自由落体是正确的，可以证明，在只有重力做功的情形下，它总是正确的。所谓只有重力做功，是指：物体只受重力，不受其他的力，如自由落体和各种抛体运动的情形；或者除重力而外还受其他的力，但其他力并不做功，物体沿光滑斜面运动就属于这种情形。

在只有重力做功的情形下，物体的动能和重力势能发生相互转化，但总的机械能保持不变。这个结论叫做机械能守恒定律，它是力学中一条重要规律，又是更普遍的能的转化和守恒定律的一个特例。

不但动能和重力势能的相互转化中机械能保持不变，在弹性势能和动能的相互转化中，如果只有弹力做功，机械能也是保持不变的。

练习六

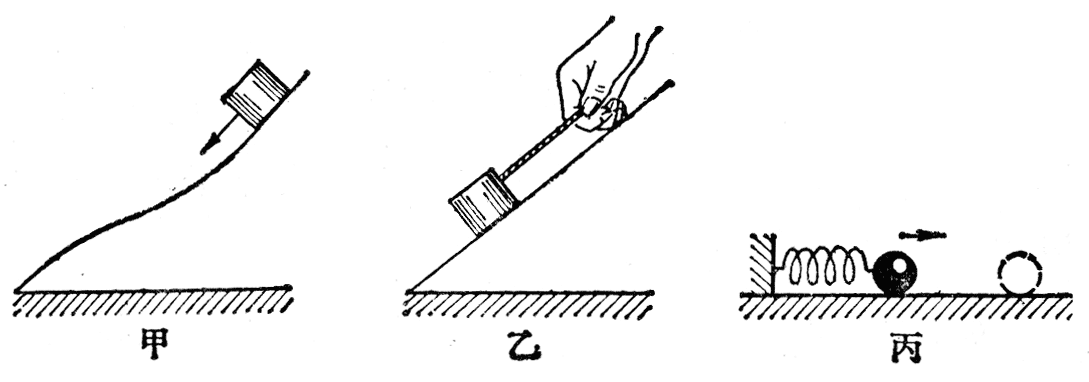
（1）在下面列举的各个实例中，除①外都不计空气阻力，哪些机械能是守恒的？说明理由。

①跳伞员带着张开的降落伞在空气中匀速下落。

②抛出的手榴弹或标枪做斜抛运动。

③用细绳拴着一个小球，绳的一端固定，使小球在光滑的水平面上做匀速圆周运动。

④用细绳拴着一个小球，绳的一端固定，使小球在竖直平面上做圆周运动。

⑤物体沿着光滑的曲面滑下（图7-21甲）。

⑥拉着一个物体沿着光滑的斜面匀速上升（图7-21乙）。

⑦在光滑水平面上运动的小球，碰到弹簧上，把弹簧压缩后又被弹簧弹回来（图7-21丙）。

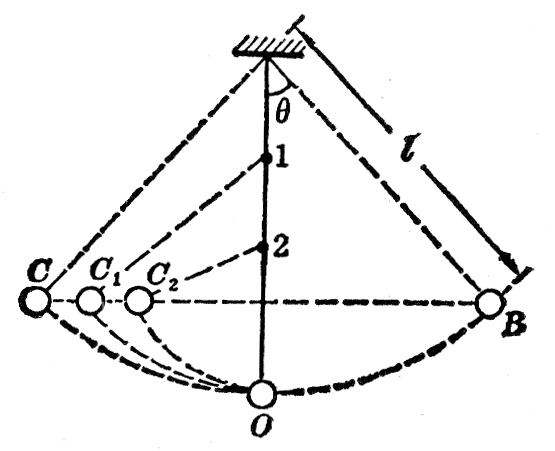
（2）做下面的实验。把物体拴在细线上悬挂起来，做成一个单摆（图7-22）。把物体从平衡位置O拉到B，放手后观察物体的来回摆动，把铅笔放在位置1和2，可以看到物体仍然要升到跟B同样高的C₁和C₂，解释这个现象。

发布时间：2015/7/30 下午4:05:08  阅读次数：2185