五、动能定理

现在我们来进一步证明，如果物体原来就是运动的，已经具有一定的动能，受到外力推动而做加速运动，速度变大，动能增加，这时外力对物体做的功将等于物体动能的增加。

设一个质量为m的物体，原来的速度是v₁，动能是\(\frac{1}{2}\)mv₁²，在恒定的外力F作用下，发生一段位移s，速度增加到v₂，动能增加到\(\frac{1}{2}\)mv₂²。设外力方向与运动方向相同，外力F对物体所做的功W＝Fs。根据牛顿第二定律，F＝ma；根据运动学公式v₂²－v₁²＝2as得到s＝\(\frac{{v_2^2 - v_1^2}}{{2a}}\)，所以

Fs＝ma×\(\frac{{v_2^2 - v_1^2}}{{2a}}\)＝\(\frac{1}{2}\)mv₂²－\(\frac{1}{2}\)mv₁²

或    W＝E_k2－E_k1。

可见，外力对物体所做的功的确等于物体动能的增加。

上面我们设外力方向与运动方向相同，导出了关系式W＝E_k2－E_k1。这个结论对外力方向与运动方向相反的情形同样适用。在这种情形下，外力所做的功是负值，而物体的运动速度减小，动能的增加也是负值。我们知道，外力对物体做负功，往往说成物体克服这个力做了功，因此，对这种情形，也可以说物体克服阻力所做的功等于动能的减少。例如在粗糙平面上运动的小车，在滑动摩擦力的作用下速度减小，这时动能的减少就等于它克服摩擦力所做的功。

上述结论是假定物体只受一个力而推导出来的；如果物体不只受到一个力，而是受到几个力，上述结论仍旧正确。只是外力所做的功是指各个力所做的功的代数和，即外力所做的总功。这样，我们得到结论：外力对物体所做的总功等于物体动能的增加。这个结论叫做动能定理。

动能定理是力学中一条重要规律，经常用来解决有关的力学问题。下面举一个例题来说明。

【例题】一架喷气式飞机的质量为5.0×10³kg，受到的推力为1.8×10⁴N，受到的阻力是它的重量的0.020倍，起飞速度为60m/s。求起飞时滑跑的距离。

飞机在水平方向受到的外力是推力F和阻力f，在外力作用下飞机在跑道上滑跑一段距离s，速度达到起飞速度v。飞机原来是静止的，E_k1＝0，而E_k2＝\(\frac{1}{2}\)mv²。阻力f＝0.020×5.0×10³×9.8N＝9.8×10²N。根据动能定理得到

Fs－fs＝\(\frac{1}{2}\)mv²

所以

\[s = \frac{{m{v^2}}}{{2(F - f)}} = \frac{{50 \times {{10}^3} \times {{60}^2}}}{{2 \times (1.8 \times {{10}^4} - 9.8 \times {{10}^2})}}m = 5.3 \times {10^2}m\]

这个例题也可以应用牛顿第二定律和运动学公式来解，请同学们自己做一下。动能定理的公式是在牛顿运动定律和运动学公式的基础上推导出来的，所以同一个题目用这两种方法来解，求得的结果是相同的。由于动能定理不涉及物体运动过程中的加速度和时间，因此应用它来解题往往比较方便。

从例题可以看出，在利用动能定理来解力学问题的时候，先要分析物体的受力情况，并据此列出各个力所做的功，然后即可利用动能定理来求解。

练习四

（1）使一个物体的速度从零增加v，再从v增加到2v。哪种情况下做的功要多些？为什么？

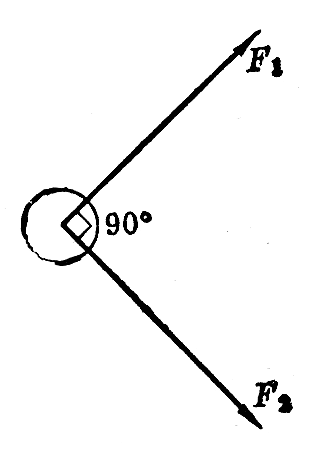
（2）在光滑平面上的物体受到沿着平面的两个力F₁和F₂的作用（图7-7）。在下列情况下，从静止开始移动2m时，物体获得的动能各是多大？①F₁＝10N，F₂＝0；②F₁＝0，F₂＝10N；③F₁＝F₂＝5N。

（3）一个30N的力水平地作用在2.0kg的物体上，使它在无摩擦的水平面上移动了3.0m的距离。然后，这个力变到15N，又使物体移动了2.0m，物体增加的动能总共是多少？

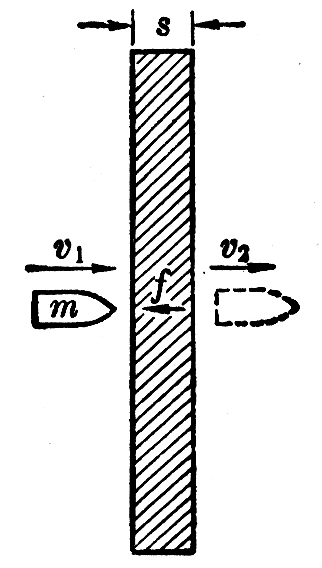
（4）质量是2.0g的子弹，以300m/s的速度水平射入厚度是10mm的钢板（图7-8），射穿后的速度是100m/s，子弹受到的平均阻力是多大？

（5）一架新型喷气式战斗机的质量是1.50×10⁴kg，发动机的推力是1.11×10⁵N，起飞速度是88.0m/s，滑跑距离是671m。计算飞机起飞时受到的平均阻力。

发布时间：2015/7/26 下午1:41:05  阅读次数：1129