第六章 六 稳度
各种建筑物,工厂的烟囱,桌子、椅子、柜橱等家具,都是有支面的物体。有支面物体的平衡是稳定平衡。这是因为物体稍微偏离平衡位置,它的重心总要升高,重力的作用线还会通过支面,重力对作为转动轴的O轴的力矩将使物体回到原来的位置,恢复平衡。只有偏离平衡位置大一些,重力的作用线不再通过支面,重力的力矩才会使物体继续远离原来的位置而倾倒(图6 -18)。
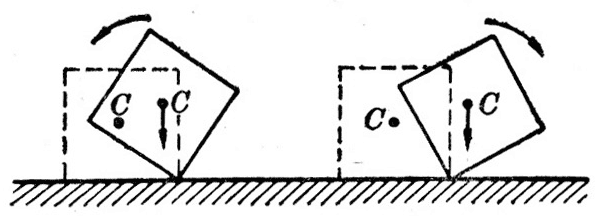
平放的砖和竖放的砖都处于稳定平衡,它们是不是还有什么区别呢?区别在于它们稳定程度不同。竖放的砖容易使它的重力作用线超出支面,容易倾倒,稳定程度较小;平放的砖不容易使它的重力作用线超出支面,不容易倾倒,稳定程度较大。
稳定程度的大小通常用稳度来表示。稳度的大小跟物体重心的高低和支面的大小都有关系。
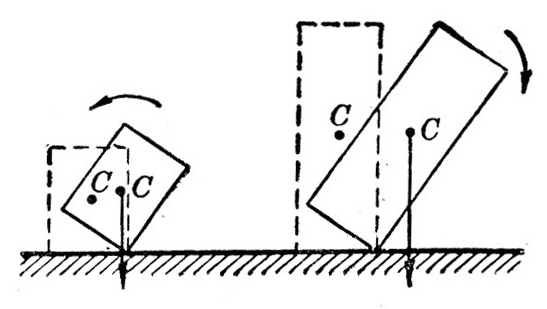
拿两个支面大小相同而重心高度不同的长方体来。如果使它们倾斜某一相同的角度(图6-19),可以看到:重心低的长方体的重力作用线可以仍旧通过支面,而重心高的长方体的重力作用线不再通过支面。可见,物体的重心越低,稳度越大。
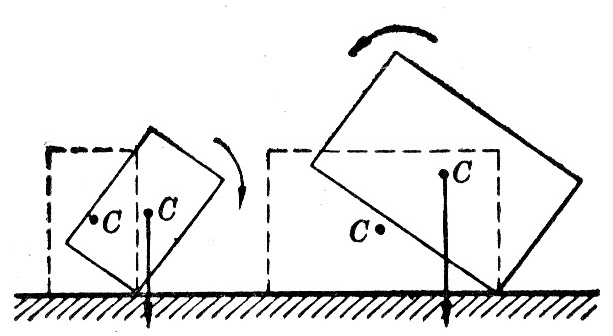
再拿两个重心高度相同而支面大小不同的长方体来。如果使它们倾斜某一相同的角度(图6-20),可以看到:支面大的长方体的重力作用线可以仍旧通过支面,而支面小的长方体的重力作用线不再通过支面。可见,物体的支面越大,稳度越大。

这里应该说明一下,所谓支面不一定如同长方体那种情形是指长方体跟支持物的实际接触面。桌子是四条腿着地的,桌子的支面是指四条桌腿所围成的矩形;三角架是三条腿着地的,它的支面是指以这三条腿为顶点所围成的三角形(图6-21)。
增大物体的稳度在实际中有重要意义。为了增大物体的稳度,可以降低重心的高度或者增大支面的面积,也可以同时降低重心的高度和增大支面的面积。许多机器、仪器、设备不能做得“头重脚轻”,而要做得底部较重底座较大,如实验用的天平安置在支面较大而且较重的底座上,实验用的铁架有一个支面较大的铸铁座,都是为了增大稳度。设计汽车、电车等交通工具,要考虑到尽可能降低重心的高度。装载车船,要把重货放下面,轻货放上面,使重心降低。照相机和某些测量仪器安置在支面相当大的三角架上,高压电线的铁塔有相当大的支面,都是为了增大稳度。
练习四
(1)背上背着重东西的人,为什么要向前倾?
(2)老年人扶手杖走路为什么不容易跌倒?
(3)用载重汽车装运木箱,一些木箱装的是铁钉,另一些木箱装的是铝制器皿。怎样装木箱,汽车的稳度比较大?
(4)下列情况是哪类平衡?①体操运动员在吊环上做倒立;②体操运动员吊在吊环上;③杂技演员走钢丝;④轮子套在水平轴上。
(5)把一个长方体立在一块木板上。在长方体前表面的中心点固定一个小螺钉,在小螺钉上拴一个小铅锤,把木块的一端慢慢抬起,研究一下长方体在什么条件下才倾倒?已知前表面的边长,你能否算出木块要抬起多大角度,长方体才倾倒?实际算一算,再用实验来检验。
复习题
(1)在共点力作用下物体的平衡条件是什么?
(2)什么叫做力矩?力对物体的转动作用决定于什么?
(3)有固定转动轴的物体的平衡条件是什么?
(4)什么叫做力偶?力偶的作用是什么?什么叫做力偶矩?力偶的转动作用决定于什么?
(5)在重力和支持力作用下物体的平衡有哪几种?这几种平衡有什么区别?
(6)什么叫稳度?稳度跟什么有关系,是怎样的关系?怎样增大物体的稳度?举出一些实例来。
习题
(1)图6-22表示一种简易起重机。OA是钢绳,跟水平方向成30°角。OB是撑杆,跟水平方向成60。角。提起的货物重5.0×103N。求钢绳对货物的拉力和撑杆对货物的支持力。
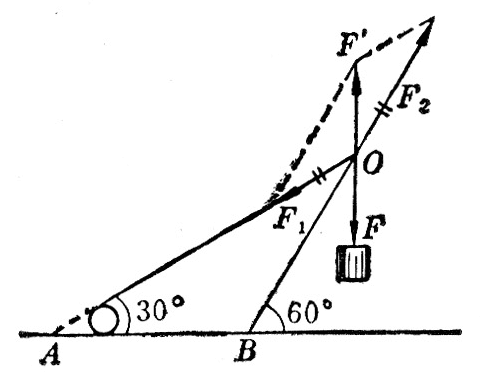
解:取O点作为受力点。O点受到三个力:货物的拉力F(等于货物的重量),钢绳的拄力F1,撑杆的支持力F2。O点在这三个力的作用下保持平衡。
应用平行四边形法则求出力F1和F2的合力Fʹ。从平衡条件知道,力Fʹ应该与F大小相等方向相反。从学过的几何知识可以证明,△OFʹF1是等腰三角形,它的两个等角是30°。
应用等腰三角形的性质可以求出F1:F1=Fʹ=F。即F1=5.0×103N。
应用正弦定理可以求出F2:
\[\frac{{{F_2}}}{F} = \frac{{\sin 120^\circ }}{{\sin 30^\circ }}\]
F2=\(\frac{{\sin 120^\circ }}{{\sin 30^\circ }}\)F=8.5×103N。
这个题也可以用力的分解来求解。但是求解物体平衡的问题,一般还是应用平衡条件为好,因为不管受力情况怎样复杂,平衡条件都适用。
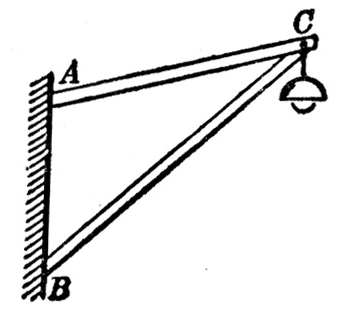
(2)在图6-23所示的支架中,梁AC长0.m米,梁BC长1.2m。AB之间的距离是0.6m,在C处挂一盏重20N的电灯。求AC对电灯的拉力和BC对电灯的支持力。
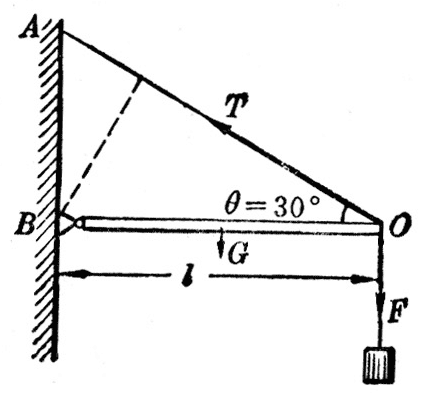
(3)图6-24中的BO是一根横梁,一端安在轴B上,另一端用钢绳AO拉着。在O点挂一个重物,重量是240N。横梁是均匀的,它本身的重量是80N。求钢绳的拉力。
解:取横梁BO作为研究对象。横梁的一端安在轴B上,是一个有固定转动轴的物体。力F的力矩是Fl,力T的力矩是Tlsinθ,自重G的力矩是Gl/2。应用有固定转动轴物体的平衡条件得到:
Tlsinθ-G\(\frac{l}{2}\)-Fl=0,
T=(G+2F)/2sinθ=560N。
在这个题里,如果把力F沿AO和OB方向分解来求钢绳的拉力,就会得到错误的结果。因为对钢绳的拉力T不仅跟物体的重量有关,而且跟横梁的自重有关。这时力F在AO方向的分力没有实际意义。
(4)一根木料,抬起它的右端要用480N竖直向上的力,抬起它的左端要用650N竖直向上的力。这根木料有多重?
(5)放在斜面上的一个物体,当斜面倾角为θ时,它沿着斜面匀速下滑。试证明物体和斜面之间的滑动摩擦系数μ=tanθ。
(6)如果天平的两臂并不完全相等,可以采取所谓复称法求得物体的真实质量m。先把物体放在左盘,砝码放在右盘,天平平衡时砝码的质量是m1。然后把物体放在右盘,砝码放在左盘,天平平衡时砝码的质量是m2。试证明物体的真实质量m=\(\sqrt {{m_1}{m_2}} \)。
(7)无风的时候竖直下落的雨滴受到两个力的作用:重力,空气阻力。设空气阻力f与雨滴下落的速度v成正比,即f=kv。开始下落时雨滴的速度较小,空气阻力也较小,雨滴加速下落,速度越来越大。随着速度的增大,空气阻力也增大。当空气阻力增大到与重力平衡时,雨滴就以一定的速度匀速下落。这个速度叫做极限速度或收尾速度。设雨滴的质量为m,试证明雨滴的极限速度v=mg/k。
(8)用斜向上方的拉力拉着一个物体在水平面上匀速前进,巳知拉力跟水平面成30°角,拉力的大小是200N,物体的重量是500N。求物体和水平面间的滑动摩擦系数。
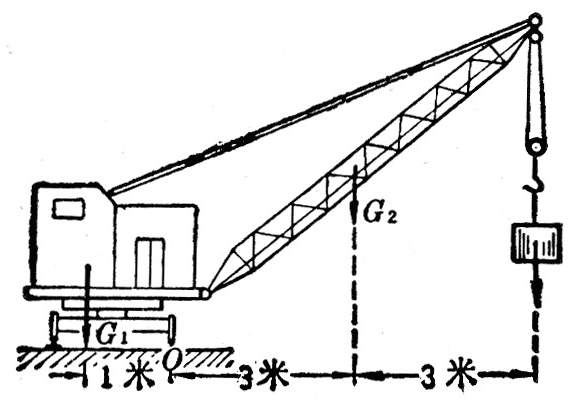
(9)图6-25是一台起重机的示意图,机身和平衡体的重量G1=4.2×105N,起重杆的重量G2=2.0×104N牛。其他数据如图中所示。起重机至多能提起多重的货物。
提示:这时起重机以O为转动轴而保持平衡。
(10)图6-26是一把杆秤。提扭和挂钩的距离OB是6.0cm,秤锤的质量是1.2斤。不称物体时,把秤锤挂在A点,杆秤平衡,A点就是刻度的起点。设OA为1.6cm,杆秤的质量为0.48斤,求杆秤的重心。在称某一物体时,秤锤移到O点后杆秤平衡,AD为24cm,所称物体的质量是多少?

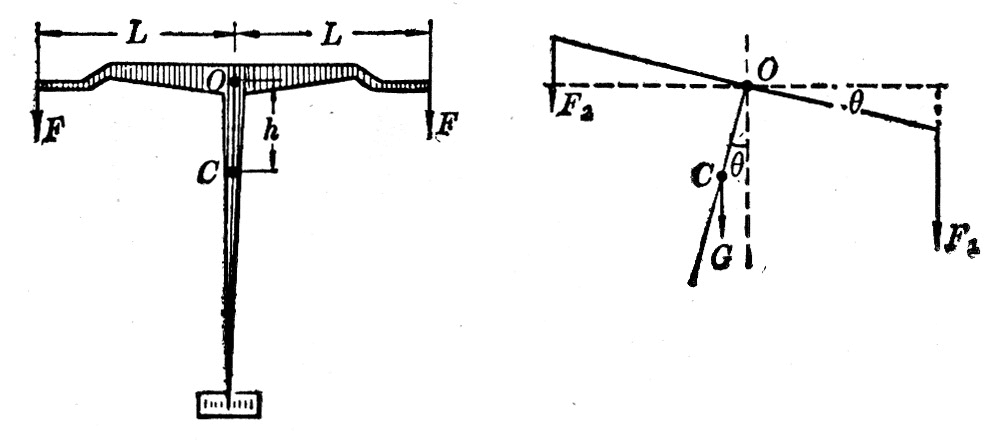
(11)天平的横梁(连同指针)是一个有固定转动轴的物体,转动轴就是中央刀口O(图6-27)。横梁的自重为G,重心C在指针上离转动轴O为h的地方。天平两盘中的重量相等时,作用在横梁两端的力F相等,横梁平衡,指针指在标尺的中央,即指针停在竖直方向。天平两盘中的重量稍有不等,横梁就要倾斜,指针随着偏移到较轻的一方,自重G对转动轴O的力矩将阻止横梁倾斜,最后横梁在某一倾斜位置上达到平衡,设指针与竖直方向成θ角时横梁平衡,可以证明
\[\tan \theta = \frac{L}{{Gh}}({F_1} - {F_2})\]
从上式可以看出,对于天平两盘中一定的重量差,G和h越小,则θ角越大,这种天平越灵敏。所以通常灵敏的天平要选用轻质材料做横梁,并要提高重心的高度。
试应用有固定转动轴的物体的平衡条件证明上式。
(12)图6-28表示拖拉机(或汽车)在上坡。拖拉机前后轮的轮距是L,重心的高度是h,重心至前轮的距离是l。可以证明,上坡时不致向后翻倒,路面的最大倾角θ1满足条件:
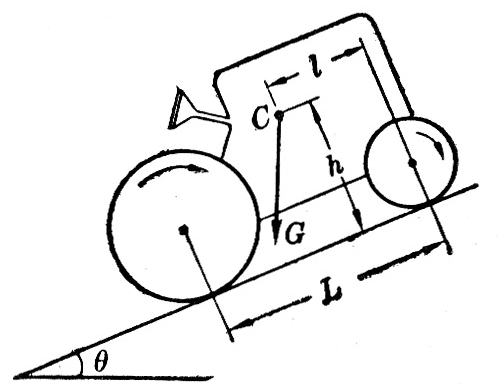
\[\tan {\theta _1} = \frac{{L - l}}{h}\]
拖拉机下坡时,可以证明,下坡时不致向前翻倒,路面的最大倾角θ2满足条件:
\[\tan {\theta _2} = \frac{l}{h}\]
试证明上两式,并根据上两式讨论:重心太高、太靠前、太靠后有什么不好?
文件下载(已下载 907 次)发布时间:2015/7/20 下午1:49:22 阅读次数:8894
