六、人造地球卫星

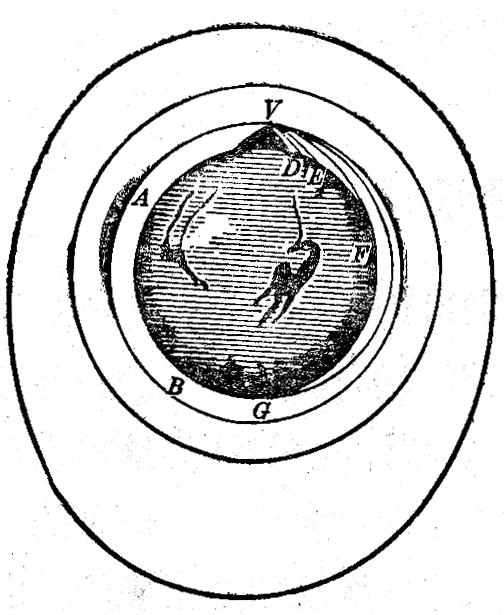
在第四章平抛运动里我们讨论过，在地面上高度是h的一点，以初速度v向水平方向抛射的物体，将沿着抛物线轨道落在地平面上。在讨论这种运动时，我们认为地球表面是一个理想的平面，重力加速度的方向和大小都是恒定的。在初速度比较小、物体的射程不大时，这样处理是正确的。由于地球实际上是一个球体，如果物体的初遮度比较大、射程比较远，上述处理就不准确了。当抛出的物体沿曲线轨道下落时，地面也沿着球面向下弯曲，重力的方向也跟着改变了，牛顿在研究天空中卫星的运动和地面附近的落体运动的关系时，讨论过这个问题。图5-5是在他的著作里画的一幅原理图。图中表示出从高山上用不同的水平速度抛出的物体轨迹，物体的速度越大，落地点离山脚越远。当速度足够大时，物体将环绕地球运转，成为一个人造地球卫星。

宇宙速度      既然物体的速度足够大时，物体将环绕地球运转，成为一个人造地球卫星，那么物体的速度究竟要多大才行呢？计算人造地球卫星的速度，需要运用牛顿运动定律和万有引力定律。设质量是m的卫星在离地心r的高空环绕地球运转，它的速度是v。地球的质量是M，卫星做匀速圆周运动所需要的向心力是地球对它的引力，即

\[G\frac{{Mm}}{{{r^2}}} = m\frac{{{v^2}}}{r},v = \sqrt {\frac{{GM}}{r}} \]

从上式可以看出，r越大，即卫星离地面越高，它环绕地球运动的速度v越小。对于靠近地面运转的卫星，可以认为r差不多等于地球的半径R_地，地球对卫星的引力差不多等于卫星的重量mg。从mg＝m\(\frac{{{v^2}}}{{{R_地}}}\)可以得到

\[v = \sqrt {g{R_地}} \]

将g＝0.0098km/s²和R_地＝6400km代入上式，得到v＝7.9km/s。这就是人造地球卫星在地面附近环绕地球做匀速圆周运动必须具有的速度，叫做第一宇宙速度，也叫环绕速度。

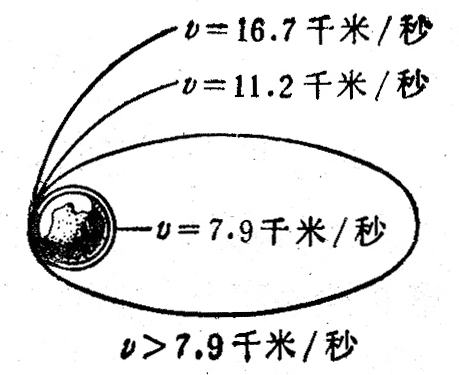
如果人造地球卫星进入轨道的水平速度大干7.9km/s，而小于11.2km/s，它绕地球运动的轨迹就不是圆，而是椭圆（图5-6）。当物体的速度等于或大于11.2km/s的时候，物体就可以挣脱地球引力的束缚，成为绕太阳运动的人造行星，或飞到其他行星上去。所以11.2km/s这个速度叫做第二宇宙速度，也叫脱离速度。

达到第二宇宙速度的物体还受着太阳引力的束缚，要想使物体挣脱太阳的束缚，飞到太阳系以外的宇宙空间去，必须使它的速度等于或大于16.7km/s，这个速度叫做第三宇宙速度，也叫逃逸速度。

三个宇宙速度的值都很大，要得到这样大的速度需要利用多级火箭。

人造地球卫星中的超重和失重 在第三章里，我们已经学过超重和失重现象。现在我们再来谈谈人造卫星中的超重和失重。

卫星发射时在加速升高的过程中，以及卫星再进入大气层向下降落的减速过程中，都有一个向上的加速度，这时就发生超重现象。这时宇宙飞行员的身体象是被一个很大的压力压住，动弹不得，想举起手来，也很困难。超重对人的生理机能也有影响。宇宙飞行员选择合适的姿态，能够在100秒钟内承受等于体重九到十倍的超重，但是超重超出一定限度就有生命危险了。

人造卫星进入轨道以后，有一个向下的加速度，因而发生失重现象。这个向下的加速度就是卫星绕地球做圆周运动的向心加速度。与升降机的情况不同的是，这个向下的加速度即向心加速度不是改变人造卫星的速度的大小，而是不断改变人造卫星的速度的方向。

人造卫星做匀速圆周运动的向心加速度，等于卫星高度处的重力加速度，所以人造卫星以及其中的人和物体都处于完全失重状态。设想地球上重力消失时地面上会发生什么现象，在人造卫星中就发生什么现象。物体将飘在空中。宇宙飞行员站着睡觉和躺着睡觉一样舒服。走路务必小心，稍有不慎，就会“上不着天，下不着地”（图5-7）。食物要做成块状（或牙膏似的糊状），进嘴后再咬，以免碎屑“掉在空中”，飞进飞行员的眼睛、鼻子里，甚至吸入气管引起生命危险。失重对入的生理机能也有某些影响。但是经过二十几年的载人航天的实践，人们知道在失重状况下应该怎么办，已经取得了在失重环境中的自由，对失重的担心已成过去。

人造卫星的应用  人造卫星的应用很广泛，可以用于无线电通讯、电视转播、军事侦察、资源调查、气象预报、科学研究等方面。应用人造卫星有什么好处呢？从下面列举的几个例子可以了解一些。

搞建设，首先必须把资源的情况摸清楚，我们搞资源调查，比如说，调查森林资源，若基本上靠人工，速度慢，效率低，二十年还查不完一遍，查到后头，前面情况早变了。资源卫星一天绕地球十几转，用来普查森林，很快就可以查完，而且可以监视各种变化，及时设法处理。在卫星上安装勘察矿产资源的遥感设备，不仅可以勘察地球表面，而且可以勘察地下的铁、钴、镍、铜、石油等多种矿藏。电视教育是多快好省地培养人才的一种手段，但是按过去的办法靠发射台和中继站传播，每隔50千米就要建设一个中继站，消耗大量的人力物力。如果用通讯卫星，象我们这样幅员广阔的国家，只要一颗卫星，全国的边远地区也都可以收看。目前我国正在积极准备发射通讯卫星。用火箭把几吨的货物送到绕地球运行的空间站上去，可以在宇宙空间建设现代化的实验室，装备复杂、精密的仪器设备，进行失重、超高真空等条件下的物理、化学、生物、医学实验。

航天时代正在到来，在这个新时代里，不畏险阻，勇攀科学高峰的青年们是可以大有作为的。

练习四

在下列各题中，地球质量取M＝6.0×10²⁴kg。

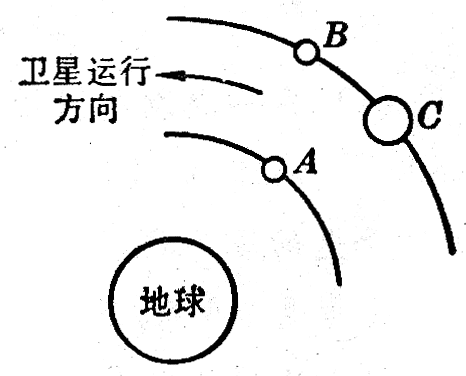
（1）图5-8中A、B、C是在地球大气层外圆形轨道上运行的三颗人造卫星。A、B的质量相同，它们的轨道速率是否也相同？B、C的质量不同，它们的轨道速率是否也不同？ 

（2）假定一颗人造地球卫星正在离地面700km高空的圆周轨道上运转，计算它的速率和周期。

（3）能否发射一颗周期是80分钟的人造地球卫星？说明你的理由。

复习题

（1）地心说和日心说的根本分歧是什么？

（2）开普勒在行星运动的研究上有什么重要贡献？他的行星运动三定律的内容是什么？

（3）什么是万有引力定律？万有引力定律的发现有什么重要意义？卡文迪许是怎样测量万有引力恒量的？

（4）怎样应用万有引力定律计算天体的质量？它所根据的原理是什么？

（5）地面上的重力加速度因地而异的原因是什么？

（6）怎样计算第一宇宙速度？它所根据的原理是什么？什么是第二宇宙速度和第三宇宙速度？

（7）为什么在轨道上运动的人造卫星中的人和物体都处于完全失重状态？

习题

（1）在一次测定引力恒量的实验里，已知一个质量是0.80kg的球，以1.3×10^-10N的力吸引另一个质量是4.0×10^-3kg的球。这两个球相距4.0×10^-2m。地球表面的重力加速度是9.8m/s₂，地球的半径是6400km。根据这些数据计算地球的质量。

（2）行星的质量为M，一个围绕它作匀速圆周运动的卫星的轨道半径是R，周期是T。试用两种方法求出卫星轨道上的向心加速度。

（3）应用通讯卫星可以实现全地球的电视转播。这种卫星位于赤道的上方，相对于地面静止不动，犹如悬在空中一样，叫做同步卫星。同步卫星的周期是多大？计算它的高度和速率。

（4）试用万有引力定律证明：对于某个行星的所有卫星来说，R³/T²是一个恒量，其中R是卫星的轨道半径，T是卫星的运行周期。

（5）行星的密度是ρ，靠近行星表面的卫星运行周期是T。试证明ρT²是一个普遍适用的恒量，即它对任何行星都相同。

（6）一艘宇宙飞船飞近某一个不知名的行星，并进入靠近该行星表面的圆形轨道，宇航员着手进行予定的考察工作。宇航员能不能仅仅用一只表通过测定时间来测定该行星的密度？说明理由。

（7）不考虑地球的自转，求出用地球半径R、地面重力加速度g和引力恒量G表示的地球密度的公式。

（8）用火箭把宇航员送到月球上，如果他已知月球的半径，那么他用一个弹簧秤和一个已知质量的砝码，能否测出月球的质量？应该怎样测定？

发布时间：2015/7/17 下午2:36:56  阅读次数：2289