五、地球上物体重量的变化

地球对物体的引力，是万有引力的一种表现，如果用M表示地球的质量，用R表示地球的半径，用m表示物体的质量，根据万有引力定律，物体在地球表面上受到的地球引力是F＝G\(\frac{{Mm}}{{{R^2}}}\)。物体的重量正是由这种引力产生的。

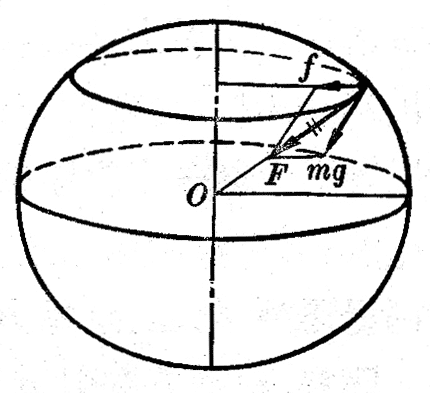
但是物体的重量并不等于地球对物体的引力，这是因为地球在不停地自转，地球上的一切物体都随着地球自转而绕地轴做匀速圆周运动，这就需要向心力。这个向心力的方向是垂直指向地轴的，它的大小是f＝mω²r，式中的r是物体距地轴的距离，ω是地球自转的角速度，这个向心力来自哪里？只能来自地球对物体的引力F，它是引力F的一个分力（图5-4）。引力F的另一个分力才是物体的重量mg。

明白了这一点，我们就容易懂得，为什么同一个物体在地球上不同纬度的地方的重量不同。

在不同纬度的地方，物体做匀速圆周运动的角速度ω相同，而圆周的半径r不同，这个半径在赤道处最大，在两极最小（等于零）。由f＝mω²r可以知道，同一个物体随着地球自转所需的向心力，在不同纬度的地方是不同的，它随着纬度的增加而减小：在赤道最大，在两极最小（等于零）。

除此之外，还应该考虑到地球并不是一个理想的球体，而是一个不大规则的椭球，它的极半径是6357千米，赤道半径是6378千米。由于极半径比赤道半径小一些，根据引力与距离平方成反比的定律，物体所受的引力在赤道上最小，随着纬度的增加而增大，在两极达到最大。

从上面的讨论可以看出，物体在赤道上所受的引力最小，需要的向心力最大；随着纬度的增加，物体受的引力增大，需要的向心力减小；在两极引力最大，需要的向心力减小到零。所以地面上同一个物体的重量，从赤道到两极是逐渐增大的。

我们知道，物体的重量等于mg。所以物体的重量从赤道到两极逐渐增大表示重力加速度g从赤道到两极逐渐增大。

同样，根据万有引力定律知道，在同一纬度，物体的重量和重力加速度g的数值，还随着离地面高度的增加而减小。

不过在地面附近，g的数值和物体的重量随纬度和离地面高度的不同而改变的量是很小的。重力加速度g的数值，在赤道上约为9.78m/s₂，在两极约为9.83m/s。把赤道上的物体移到两极，增加的重量大约只有原来重量的千分之五。把地面上的物体升高1km，减小的重量不超过原来重量的万分之三。所以在一般的粗略计算中，g和物体重量的变化可似忽略不计。

此外，物体的重量还受到地质结构的影响。例如，在埋藏着密度较大的矿石的地区，物体的重量就要比周围地区稍大一些，也就是说，这一地区的重力加速度要比周围地区稍大一些。重力加速度的这种变化虽然很小，却是可以测出来的。根据这种重力异常现象，可以探测地下的矿床，这种探矿方法叫做重力探矿，是一种很重要的探矿方法。

发布时间：2015/7/17 下午2:35:40  阅读次数：3830