三、万有引力恒量的测定

万有引力定律公式中的比例常数G是适用于任何两个物体的普适恒量，叫做万有引力恒量。

牛顿发现了万有引力定律，但是没有给出引力恒量G的数值。用实验测定G的大小是很不容易的，因为一般物体间的引力非常小，很难精确测定，所以在万有引力定律发现后的百余年间，一直没有测出引力恒量的准确数值。有一些科学家，为了测出物体间的引力，曾利用山峰、海岛等质量大的物体做过实验，但都没有取得令人满意的结果。

1798年，即在牛顿发现万有引力定律一百多年以后，英国的卡文迪许（1731～1810）巧妙地利用扭秤装置。第一次在实验室里比较准确地测出了万有引力恒量的数值。

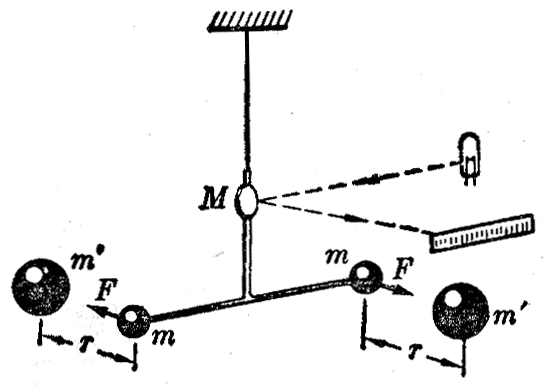
如图5-3所示，卡文迪许扭秤的主要部分是一个轻而坚固的T形架，倒挂在一根石英丝的下端。T形架水平杆的两端，各装一个质量是m的小球，在T形架的竖直杆上装一块小平面镜M，可以将射来的光线反射到一根刻度尺上。实验时，把两个质量是mʹ的大球放在图中所示的位置，它们跟小球的距离相等，由于m受到mʹ的吸引，石英丝被扭转，石英丝扭转的角度可以从小镜M的反射光在刻度尺上移动的距离求出，根据扭转角度就可以算出m与mʹ的引力F。在实验过程中，为了排除气流对测量结果的影响，卡文迪许把扭秤装置放到密闭室内，在室外用望远镜进行观测。

卡文迪许经过多次实验，证明了牛顿的万有引力定律是正确的，并且测出了万有引力恒量。如果质量的单位用千克，距离的单位用米，力的单位用牛顿，卡文迪许测得的引力恒量是6.754×10^-11N·m²/kg²，同现代公认的G等于6.67×10^-11N·m²/kg²很接近。这个数值等于两个质量各为1千克的物体，相距1米时的相互吸引力。

万有引力恒量G的数值非常小，所以我们日常接触的那些质量不是很大的物体间的引力就非常小，我们察觉不到。例如两个质量各为100g的苹果，相距10cm时，它们之间的引力大小还不到一粒砂子的重量的十万分之一，两个质量各为50kg的人相距1m时，他们之间的引力大约等于质量为百分之一毫克的物体的重量，这相当于几百粒尘埃的重量。这样小的力我们凭感觉当然是察觉不出来的。但如果物体的质量很大，这个引力就很大，例如地球的质量是很大的，它对地面上物体的吸引力就很显著，太阳和地球之间的吸引力就更大，大约等于3.56×10²²牛，这样大的力如果作用在直径是9000km的钢柱两端，可以把它拉断！正是由于太阳对地球有这样大的引力，才使得地球围绕太阳转动，而不离去。

练习二

（1）你能说出你对地球的引力是多少吗？

（2）“我们说苹果落向地球，而不说地球向上运动碰刭苹果，是因为地球的质量比苹果大得多，地球对苹果的引力比苹果对地球的引力大得多。”这种说法对吗？为什么？

（3）两个质量都是4kg的铅球，相距0.1m远，它们之间的引力是多少？

（4）用M表示地球的质量，R表示地球的半径，r_月地表示月球到地球的距离。试证明，在地球引力作用下，

①地面上物体的重力加速度g＝\(\frac{{GM}}{{{R^2}}}\)；

②月球的加速度a_月＝\(\frac{{GM}}{{r_月地^2}}\)；

③已知r_月地＝60R，利用①②求\(\frac{{{a_{月}}}}{g}\)＝？

④已知r_月地＝3.8×10⁸m，月球绕地球运行的周期T＝27.3天，计算月球绕地球运行的向心加速度a_月。

⑤巳知重力加速度g＝9.8m/s²。用④中算出的a_月，求\(\frac{{{a_{月}}}}{g}\)＝？

比较③⑤中求出的\(\frac{{{a_{月}}}}{g}\)是否相等。如果相等，则表明地球对月球的引力和对地面物体的引力都遵守平方反比定律，因而是同一种性质的力。牛顿就是根据这一结果证明地球对月球的引力和地面上物体所受的重力是同一种力的。

发布时间：2015/7/16 下午1:49:35  阅读次数：1512