九、离心现象

离心运动      要使质量是m的物体以角速度ω沿半径是r的圆周运动，就要使物体受到大小等于mω²r的向心力。当角速度ω增大时，要保持物体到圆心的距离r不变，所需的向心力必须增大，这就要相应地增大作用在物体上的合外力，但是合外力不是可以无限增大的。例如图4-21所示的物体做匀速圆周运动需要的向心力，是由绳的弹力提供的，弹力是由绳的形变产生的。物体绕圆心旋转的角速度增大时，绳的拉伸形变必须随着增大，这样才能提供足够大的向心力使物体做圆周运动。但绳的拉伸是有限度的。当角速度增大到一定程度时，绳会被拉断，弹力F就突然消失，这时物体将因惯性沿圆周的切线飞出（图4-28）,离圆心越来越远。同样，如果作用在物体上的合外力F小于它做匀速圆周运动所需的向心力，即F＜mω²r，物体也不能继续沿原来的圆周轨道运动，而要沿着一条曲线运动，离圆心越来越远（图4-28）。

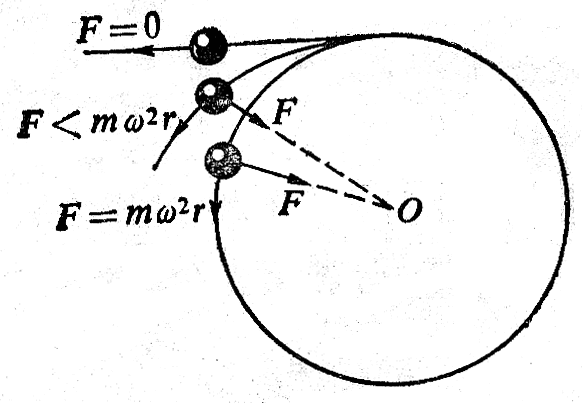
做匀速圆周运动的物体，在合外力突然消失或者合外力不足以提供所需的向心力时将做逐渐远离圆心的运动，这种运动叫做离心运动。

离心机械      利用离心运动的机械叫做离心机械。离心机械的种类很多，应用很广，下面介绍离心脱水器和离心转速计。

离心脱水器是用来甩掉湿物体上的水的装置。洗衣机里的脱水筒，纺织厂里使湿的棉纱、毛线或纺织品脱水的器械，就是这种装置。

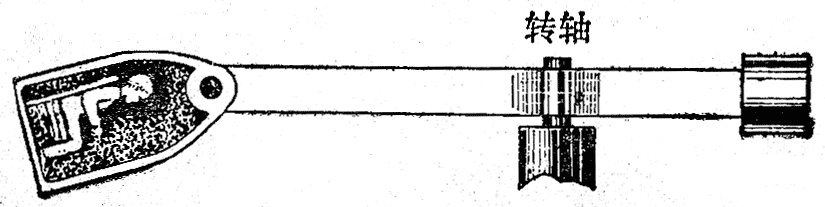
离心脱水器的主要部分是一个可以转动的筒，筒壁上有许多小孔（图4-29），湿物体就放在这个筒里，当筒转动得相当快的时候，水滴跟物体间的附着力小于水滴做圆周运动需要的向心力，于是水滴离开物体，逐步远离圆心，到达筒边，穿过小孔，因惯性而沿切线飞出，这样就把湿物体上的水甩掉了。

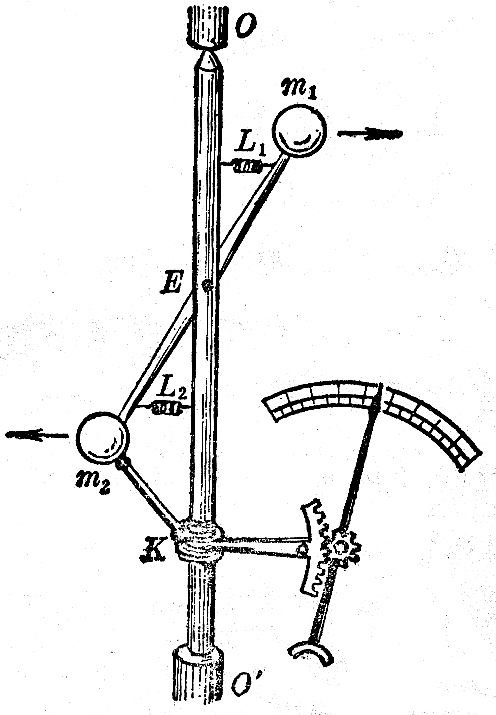
离心转速计是用来测量机器转速的一种仪器，它的构造如图4-30所示。在转速计的转轴OOʹ上的四处安装着一根轻的金属棒，棒的两端有两个重球m₁和m₂，金属棒可以绕E点转动，弹簧L₁和L₂用来把金属棒拉向转轴。滑套K可以沿转轴上下移动，把转速计的转轴OOʹ跟机器的转轴连接在一起，当机器的轴转动时，OOʹ随着转动，重球m₁和m₂跟着做圆周运动，所受的向心力是由弹簧的拉力提供的。轴转动得越快，重球做圆周运动的半径就越大，滑套K在轴上就上升得越高，同时带动指针向左偏转，从刻度盘上就可以读出机器的转速。

一些有害的离心运动 离心运动有时会造成危害，需要设法防止。高速转动的砂轮、飞轮，都不得超过允许的最大转速，如果转速过高，砂轮、飞轮内部的相互作用力小于需要的向心力，砂轮、飞轮某些组成部分的离心运动会使它们破裂，高速甩出后可能酿成事故。飞机由俯冲拉起时或者飞机翻斤斗时，飞行员的血液由于离心运动向下肢流去，造成飞行员大脑贫血，四肢沉重，这种现象叫做过荷。过荷太大时，飞行员就会暂时失明，甚至晕厥。在飞行训练和空战时过荷现象是难免的，飞行员可以依靠加强训练、增强体质来提高自己的抗荷能力。图4-31是离心试验器的原理图，它用来研究过荷对人体的影响，测验人的抗荷能力。

复习题

（1）物体做曲线运动的条件是什么？做曲线运动的物体在任一时刻的即时速度方向是什么？为什么说曲线运动总是变速运动？

（2）什么叫运动的合成，什么叫运动的分解？怎样进行运动的合成和分解？

（3）平抛运动可以看做是哪两个运动合成的？它的运动轨迹是什么曲线？怎样确定平抛物体在任一时刻的位置？

（4）斜抛运动是由哪两个分运动合成的？它的运动轨迹是什么曲线？斜抛运动跟竖直上抛运动和平抛运动之间有什么关系？

怎样确定斜抛物体在任一时刻的位置？

怎样确定斜抛物体的射高和射程？在什么情况下斜抛物体的射程最大？

（5）什么是匀速圆周运动？描述匀速圆周运动的快慢有哪几个物理量，它们之间的关系是怎样的？

（6）为什么做匀速圆周运动的物体需要有一个向心力？在分析做圆周运动物体的受力情况时，有的同学往往错误地认为，这个物体除了受到另外物体对它的作用力，还受到一个向心力。这样来分析，为什么是错误的？复习课文中讲过的和你自己做过的分析向心力的实例，并加以总结。

（7）怎样计算向心加速度和向心力的大小？物体的向心加速度和所受的向心力跟哪些因素有关系？写出向心加速度和向心力的不同形式的公式，并说明它们之间的关系和各自的物理意义。

（8）什么叫离心运动？试举一两个例子说明它的应用。

习题

（1）汽艇在静水中的速度是10km/h，渡河时向着垂直于河岸的方向匀速行驶。现在河水的流速是3km/h，河宽500m，汽艇驶到对岸需要多长时间？汽艇在河水中实际行驶的距离是多大？

（2）在490m的高空，以240m/s的速度水平飞行的轰炸机，追击一鱼雷艇，该艇正以25m/s的速度与飞机同方向行驶。试问，飞机应在鱼雪艇后面多远处投下炸弹，才能击中该艇？

（3）两人传球，如果球从一个人手里到另一个人手里经过的时间是2s，球到达的最高点离手有多高？（设两人的手等高）

（4）从仰角是30°的枪筒中射出的子弹，初速度是600m/s。求子弹在轨迹最高点和落地点的速度各是多大。

（5）伽利略曾说过：“仰角（即抛射角）比45°增大或减小一个相等角度的抛体，其射程是相等的，”你能证明这个说法的正确性吗？

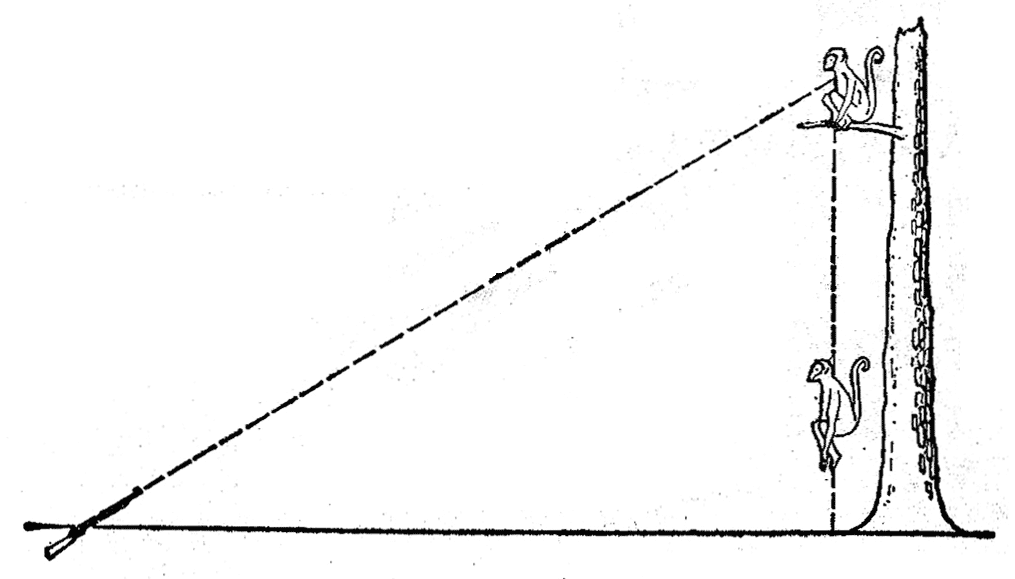
（6）一个人站在地面上用枪对准树上的猴子（图4-32），当子弹从枪口射出时，猴子立即从树上竖直下落（初速度为零）。讨论一下，猴子能否避开子弹的射击。

提示：斜抛运动可以看作是物体沿初速度方向所做的匀速直线运动和在重力作用下的自由落体运动的合运动。

（7）飞机从俯冲刭拉起的一段轨迹是一段圆弧（参看图4-19），如果飞机在这段弧上的速率是540km/h，要使它在最低点时的向心加速度不超过5g。圆弧的半径至少是多少米？（g取10m/s²）。

（8）一个35kg的重物，系在2.0m长的悬绳下端，不断摆动。重物通过最低点时的速率是3.0m/s，求这时绳对物体的拉力。

（9）要使小球滑到圆形轨道顶端时不掉下来（图4-33），小球在轨道顶端的最小速率应是多大？已知圆形轨道的半径为R。

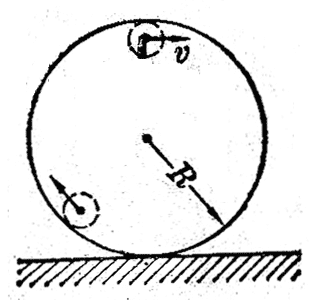
解：小球在圆形轨道顶端时受到的力有两个：重力和轨道对小球的压力，它们的方向都是竖直向下的。这两个力的合力就是小球做圆周运动通过轨道顶端时所受的向心力。小球受到的重力是固定不变的。轨道对小球的压力跟小球通过轨道顶端时的速率有关系，速率越小，小球所需的向心力越小，轨道对小球的压力就越小。当速率小到某一数值时，轨道的压力减为零，小球所需的向心力仅由重力提供，这个速率就是小球滑到轨道顶端时不掉下来的最小速率。如果速率再小，小球所需的向心力小于它受到的重力，小球将脱离圆形轨道而掉下来。

设小球通过轨道顶端时的最小速率为v，这时小球所需的向心力等于\(m\frac{{{v^2}}}{R}\)。由以上的分析可知，要使小球不掉下来，向心力必须满足下式：

\[mg = m\frac{{{v^2}}}{R}\]

所以

\[v = \sqrt {Rg} \]

（10）一个滑雪者连同他的滑雪板质量共70kg，他滑到凹形的坡底时的速度是20m/s，坡底的圆弧半径是50m，计算在坡底时雪地对滑雪板的支持力。

（11）一辆600kg的汽车以10m/s的速度通过圆弧半径是30m的山坡顶点时，汽车受到哪几个力的作用？汽车对路面的压力是多大？

发布时间：2015/7/12 上午9:12:33  阅读次数：4639