八、匀速圆周运动的实例分析

下面我们分析两个匀速圆周运动的实例，通过这两个例子，说明在具体问题中怎样分析物体受到的向心力，以及如何运用向心力来研究物体做匀速圆周运动的情况。

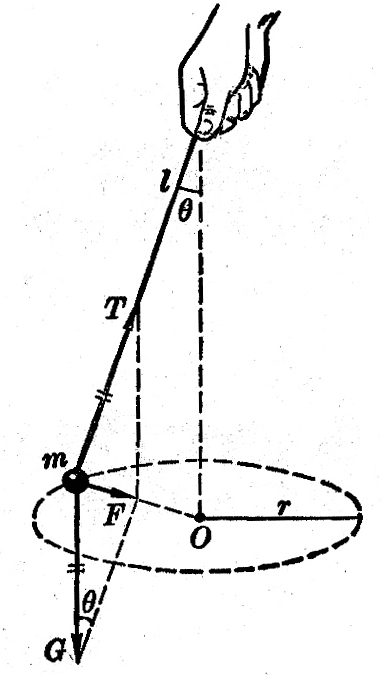
圆锥摆   在长度是l的细绳下端拴一个质量是m的小球，捏住绳子的上端，使小球在水平面内做圆周运动，细绳就沿圆锥面旋转，这样就成了一个圆锥摆（图4-24）。增大小球绕圆心O匀速旋转的角速度ω，可以看到绳跟竖直方向的夹角θ随着增大。圆锥摆的运动情况为什么会这样，我们可以从分析小球受力情况来得到解答。

做匀速圆周运动的小球m受到地球对它的重力G和绳对它的拉力T的作用，G和T的合力F就是使m产生向心加速度的向心力。从图4-24可以看出向心力F＝Gtgθ＝mgtgθ，r＝lsinθ。把F和r的表示式代入向心力的公式F＝mω²r中，得到mgtgθ＝mω² lsinθ。这样，我们就可以得到θ和ω的关系：

\[\cos \theta = \frac{g}{{{\omega ^2}l}}\]

从上式我们看出，ω的值越大，即球旋转的角速度越大，cosθ的值就越小，角θ就越大，θ在0到\(\frac{\pi }{2}\)范围内变化。

火车转弯      在平直的铁轨上匀速行驶的火车受到四个力的作用：重力、铁轨的支持力、机车的牵引力、空气及铁轨的阻力。前两个力互相平衡，后两个力也互相平衡，火车处于平衡状态，做匀速直线运动。在火车转弯处，是什么力打破了火车的平衡状态使它产生向心加速度呢？

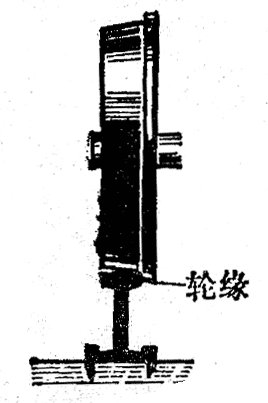
大家注意过吗？火车的车轮上有凸出的轮缘（图4-25）。当火车在平直轨道上匀速行驶的时候，轮缘并不与铁轨相互作用。在火车转弯处，如果内外轨一样高，外侧车轮的轮缘就挤压外轨，轮缘和铁轨都发生弹性形变，而产生相互作用的弹力。外轨作用在轮缘上的弹力Fʹ，就是指向圆心使火车产生向心加速度的向心力（图4-26）。一如果火车转弯时的速率是v，转弯处弧形轨道的半径是r，火车的质量是m，那么

\[F' = m\frac{{{v^2}}}{r}\]

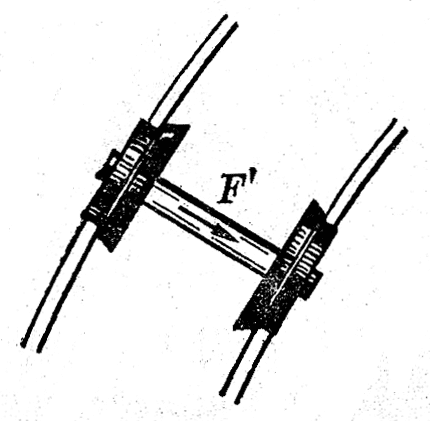
火车的质量和速率都相当大，Fʹ也相当大，根据牛顿第三定律，外侧车轮的轮缘向外挤压外轨的力跟Fʹ大小相等、方向相反。外轨在这个力的挤压下很容易损坏。怎样才能减小轮缘跟铁轨相互挤压的力而又能产生使火车转弯所需的向心力呢？

我们可以使路面向圆心一侧倾斜一个很小的角度，使外轨略高于内轨（图4-27），这时支持力N不再与重力G平衡，它们的合力F指向圆心，这个合力F和外轨对轮缘的弹力Fʹ的共同作用，使火车产生向心加速度\(\frac{{{v^2}}}{r}\)。可见外轨略高于内轨时能减小外轨与轮缘间的作用力。

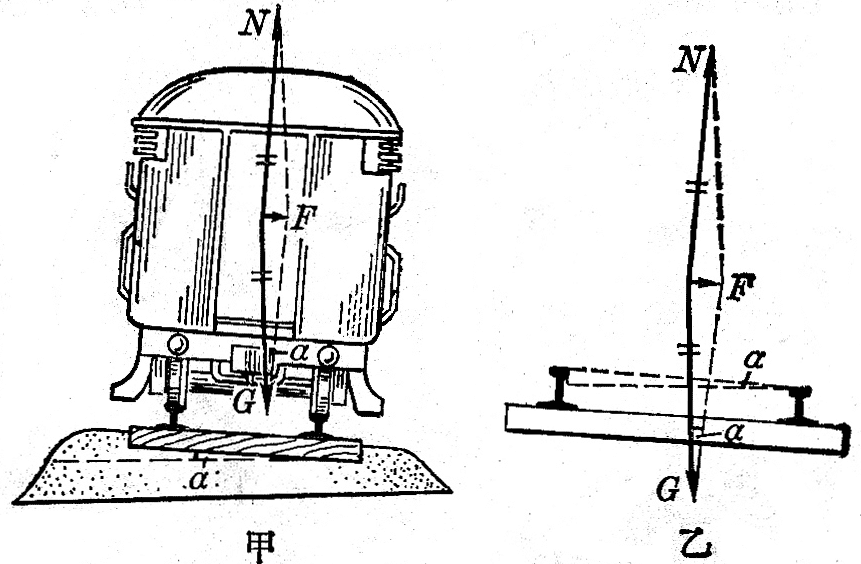
如果外轨超出内轨的高度适当，可以使重力G与支持力N的合力F刚好等于火车转弯所需要的向心力\(\frac{{m{v^2}}}{r}\)。这时Fʹ＝0，即外轨与轮缘不相互挤压。在修筑铁路的时候，正是根据转弯处轨道的半径r和规定的行驶速率v，选择适当的路面倾斜角度α，或者说选择适当的内外轨高度差h，来使Fʹ＝0。对于已经修筑好的铁路，转弯处的r和h已经定了，如果火车速率超过规定的速率，F将小于需要的向心力，所差的仍需由外轨对轮缘的弹力来弥补。如果火车的速率小于规定的速率，F将大于需要的向心力，超出的则由内轨对内侧车轮轮缘的弹力来平衡。

练习八

（1）在图4-24的圆锥摆中，如果线和垂直方向成30°角，小球在水平面内做每分钟60转的匀速圆周运动，线的长度是0.28m，计算重力加速度的值。

（2）有人说：“图4-24中的圆锥摆少画了一个作用在小球上的力，这个力与F大小相等、方向相反，是F的平衡力。必须有这个力，小球才能处于平衡状态而不落向圆心。”这种说法错在哪里？

（3）铁路转弯处圆弧的半径是300m，轨距是1435mm，规定火车通过这里的速度是72km/h，计算内、外铁轨的高度差。

（4）一架滑翔机用180km/h的速率，沿着半径为1200m的水平圆弧飞行，计算机翼和水平线的夹角（参阅图4-22）。

发布时间：2015/7/12 上午9:11:14  阅读次数：1903