七、向心力

做匀速圆周运动的物体具有向心加速度，从牛顿运动定律知道，这个加速度不会凭空产生，一定是外力对物体作用的结果，在前一节里，我们已经求出了向心加速度的大小，根据牛顿第二定律，就可以求出使物体产生向心加速度的外力的大小：

F＝ma_n＝m\(\frac{{{v^2}}}{r}\)，

或

F＝ma_n＝mω²r。

我们知道，向心加速度的方向是指向圆心的，加速度的方向跟力的方向又总是一致的，所以使物体产生向心加速度的力的方向也一定是指向圆心的。因此，习惯上常把使物体产生向心加速度的力叫做向心力。

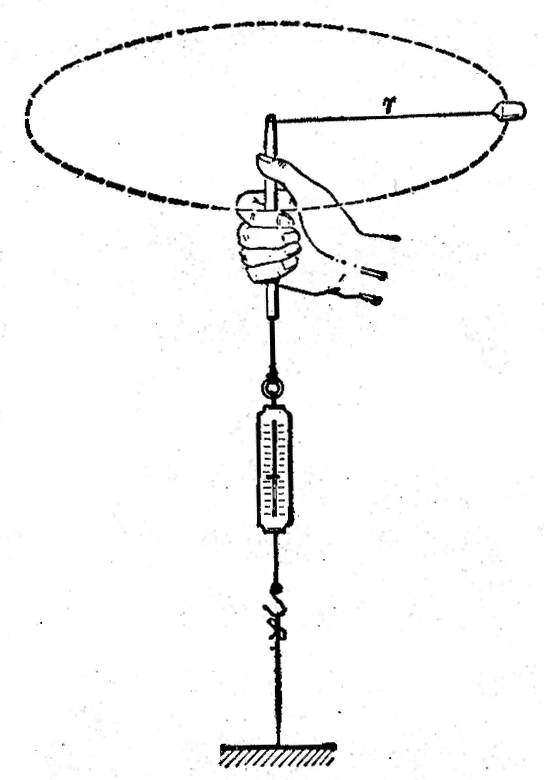
上述计算向心力的公式，可以用实验粗略地验证。让尼龙线穿过圆珠笔杆，线的一端拴一只橡皮塞，另一端拴在弹簧秤上，然后握住笔杆，象图4-20那样平稳地旋转橡皮塞，使它做水平圆周运动。这时，使橡皮塞做匀速圆周运动的向心力是尼龙线的拉力，它的大小可以从弹簧秤读出。保持圆周半径r不变，加快旋转，即增大角速度和线速度，从弹簧秤上可以看出，向心力随着增大。保持角速度不变，改变半径，会看到半径增大时向心力也随着增大。

必须注意，使物体做匀速圆周运动的向心力不是什么特殊的力，任何一种力或几种力的合力，只要它能使物体产生向心加速度，它就是物体所受的向心力。

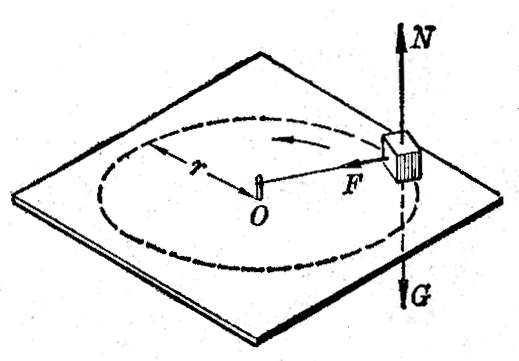
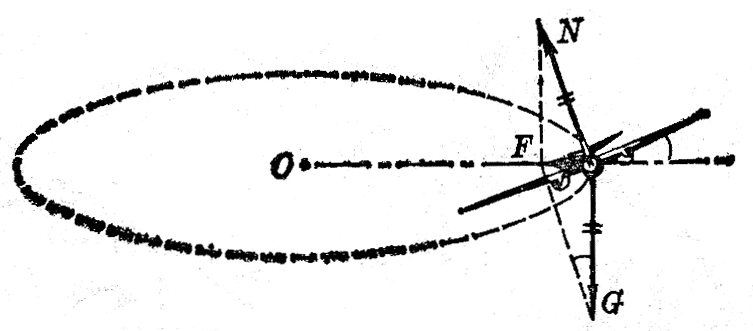
例如，系于绳子一端的物体在光滑水平面上绕O点做匀速圆周运动时（图4-21），物体所受的向心力是绳子的拉力F（重力G与支持力N平衡）。通讯卫星绕地球做匀速圆周运动时卫星所受的向心力是地球的引力（参看第五章）。飞机绕水平圆周盘旋时要向圆周内侧倾斜（图4-22），这时使飞机产生向心加速度的力是升力N和重力G的合力。

分析做匀速圆周运动的物体的受力情况时，首先要分析清楚这个物体受到哪些物体的作用力，只要物体是做匀速圆周运动，这些作用力的合力就一定指向圆心，就是使物体产生向心加速度的向心力。

阅读材料：力的分解与曲线运动

我们知道，物体所受合外力的方向如果跟物体的速度方向在一直线上，合外力只改变速度的大小，不改变速度的方向，物体仍沿这条直线运动。

在圆周运动的学习中，我们又看到另外一种情况：跟物体速度方向垂直的合外力（向心力），只改变速度的方向，不改变速度的大小。

把这两种情况联系起来考虑，可以帮助我们进一步认识物体做曲线运动的条件。

在一般的曲线运动中，物体所受的合外力F，既不与速度方向在一直线上，又不与速度方向垂直，根据力的分解，可以把这个合外力分解成两个互相垂直的分力（图4-23甲）：一个分力F_t与速度方向在一直线上，另一个分力F_n与速度方向垂直。前一个分力只改变速度的大小，后一个分力只改变速度的方向。当F_n＝0时，合外力F等于F_t，物体的运动方向不变，做直线运动。只有F_n≠0，即合外力的方向与速度的方向不在一直线上时，物体的运动方向才会改变。

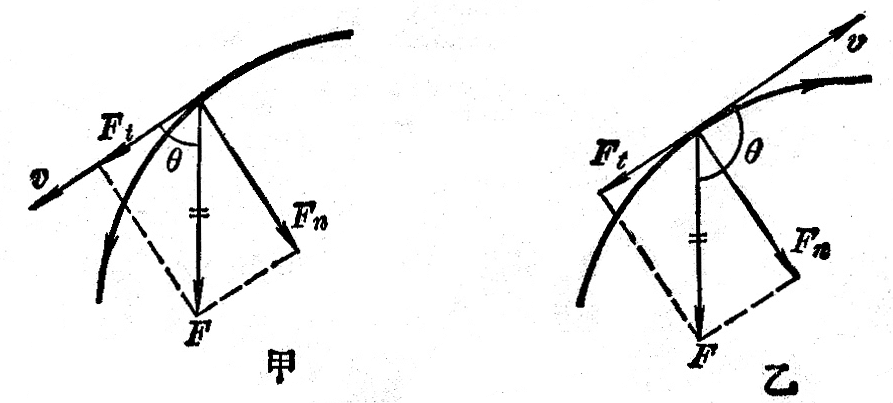
用这种方法我们还可以了解合外力的方向对曲线运动速度大小的影响。当合外力F与速度方向间的夹角θ是锐角时（图4-23甲），分力F_t与速度方向相同，物体的速度增大；当合外力F与速度方向间的夹角θ是钝角时（图4-23乙），分力F_t与速度方向相反，物体的速度减小。斜抛物体的运动，在上升阶段速度减小，在下降阶段速度增大，就是这个道理。

练习七

（1）下面的受力分析对吗？如果不对，说明错在哪里。

①图4-21中做匀速圆周运动的物体受四个力的作用，这四个力是重力、支持力、绳的拉力和向心力；

②图4-22中水平盘旋的飞机受到三个力的作用，这三个力是向心力、重力、升力。

（2）要使一个3.5kg的物体在半径是2.0m的圆周上以4.0m/s的速率运动，需要多大的向心力？

（3）太阳的质量是1.98×10³⁰kg，它离开银河系中心大约3万光年（1光年＝9.46×10¹²km），它以250km/s的速率绕着银河系中心转动，计算太阳绕银河系中心转动的向心力。

（4）甲乙两球都做匀速圆周运动，甲球的质量是乙球的3倍，甲球在半径是25cm的圆周上运动，乙球在半径是16cm的圆周上运动。在一分钟内，甲球转了30次，乙球转了75次，试比较两球所受的向心力。

（5）线的一端拴一重物，手握线的另一端使重物在水平面内做匀速圆周运动，当每分钟转数相同时，线长易断还是线短易断？为什么？线速度相同时又怎样？

发布时间：2015/7/11 上午9:37:19  阅读次数：4154