六、向心加速度

匀速圆周运动既然是变速运动，做匀速圆周运动的质点一定具有加速度，这个加速度的方向和大小是怎样的呢？

匀速圆周运动的加速度的方向 如图4-18甲所示，设质点沿半径是r的圆周做匀速圆周运动，在某时刻它处于A点，速度是v_A，经过很短的时间Δt后，运动到B点，速度是v_B。为了看清楚速度的变化情况，我们把速度矢量v_A和v_B的始端画在一起，如图4-18乙所示。根据矢量合成的三角形法可知，矢量v_A与Δv之和等于v_B。所以Δv是质点从A运动到B时速度的变化量。比值\(\frac{{\Delta v}}{{\Delta t}}\)是质点在Δt时间内的平均加速度，它的方向跟Δv的方向相同。当Δt趋近于零时，\(\frac{{\Delta v}}{{\Delta t}}\)的极限值就是质点在A点的加速度。

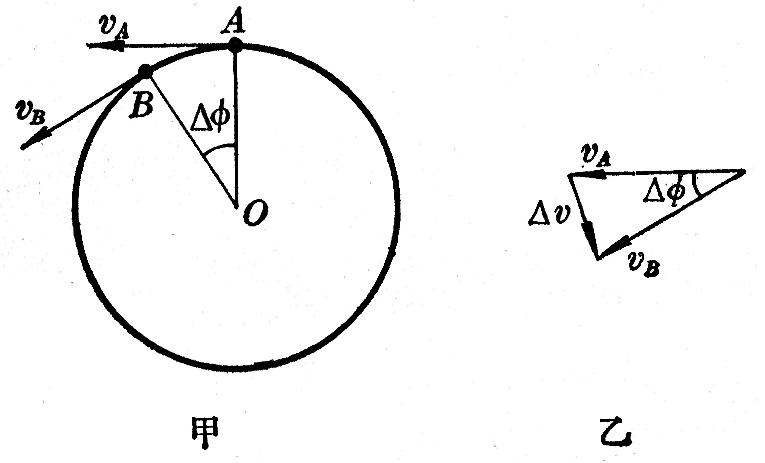
在图4-18乙所示的矢量三角形中，v_A和v_B的大小相等，当Δt趋近于零时，Δϕ也趋近于零，这时Δv便垂直于v_A。而v_A的方向是在圆周的切线上，所以Δv的方向是沿着半径指向圆心的。可见，质点做匀速圆周运动时，它在任一点的加速度都是沿着半径指向圆心的。因此，匀速圆周运动的加速度叫做向心加速度，向心加速度只改变速度的方向，不改变速度的大小。

向心加速度的大小     从图4-18中可以看出，图乙中的矢量三角形跟图甲中的△OAB是相似形，如果用v表示v_A、v_B的大小，则有

\[\begin{array}{l}\frac{{\Delta v}}{v} = \frac{{{\rm{弦AB}}}}{r}\\\Delta v = {\rm{弦AB}} \cdot \frac{v}{r}\end{array}\]

用Δt除上式两边，得

\[\frac{{\Delta v}}{{\Delta t}} = \frac{{{\rm{弦AB}}}}{{\Delta t}} \cdot \frac{v}{r}\]

当Δt→0时，\(\frac{{\Delta v}}{{\Delta t}}\)就是向心加速度的大小，我们用a_n来表示，\(\frac{{{\rm{弦AB}}}}{{\Delta t}}\)就是线速度v。于是上式变为

\[{a_n} = \frac{{{v^2}}}{r}\]

这就是匀速圆周运动的向心加速度公式。

向心加速度的大小也可以用角速度和圆周半径来表示，根据v＝ωr的关系，上式可以改写成

a_n＝ω²r。

在匀速圆周运动中，由于r、v和ω是不变的，所以向心加速度的大小不变；但是向心加速度的方向却时刻在改变，在圆周上不同点处，向心加速度的方向不同，沿着该点的半径指向圆心。而加速度是既有大小又有方向的矢量，所以匀速圆周运动是一种变加速运动。

向心加速度的公式a_n＝v²/r和a_n＝ω²r虽然是从匀速圆周运动推得的，但也适用于变速圆周运动，即线速度（或角速度）时刻改变的圆周运动。在变速圆周运动中，向心加速度的大小是随着线速度的变化（或角速度）而变化的。利用上面的公式求物体在圆周上某点向心加速度的大小时，必须用物体在该点的线速度（或角速度）的即时值。

练习六

（1）在图4-17所示的皮带传动装置中，两轮边缘上的A点和B点的向心加速度、哪个大？为什么？大轮上A点和C点的向心加速度哪个大？为什么？

（2）从a_n＝\(\frac{{{v^2}}}{r}\)看，a_n跟r成反比，从a_n＝ω²r看，a_n跟r成正比。如栗有人问你：“向心加速度的大小跟半径是成正比还是成反比？”应该怎样回答？

（3）由于地球的自转，地球上的物体都有向心加速度，试回答：

①“在地球表面各处的向心加速度的方向都是指向地心的”，这种说法正确吗？为什么？

②在赤道和极地附近的向心加速度哪个大？为什么？

③在北京的物体由于地球自转而产生的向心加速度是多大（北京的纬度取40°，地球的半径取6.4×10³km）？

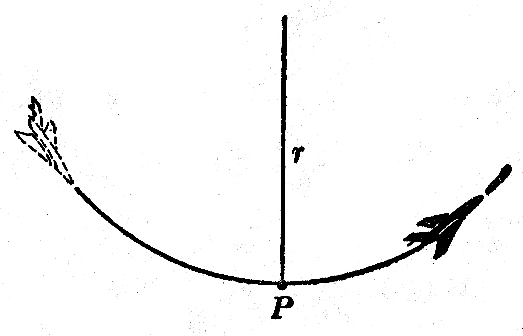
（4）飞机由俯冲转为拉起的一段轨迹可以看作一段圆弧（图4-19）。如果这段圆弧的半径r是800m，飞机在圆弧最低点P的速率为720km/h。求飞机在P点的向心加速度是重力加速度的几倍。（g取10m/s²）

（5）一个物体做匀速圆周运动，如果圆周的半径是r，运动的周期是T，试证明向心加速度a＝4π²r/T²。

发布时间：2015/7/11 上午9:31:38  阅读次数：1664