五、匀速圆周运动

轨迹是圆周的运动叫圆周运动。圆周运动是很常见的一种曲线运动。皮带轮和飞轮上各部分的运动是圆周运动，电动机转子和离心式水泵叶片上各部分的运动也是圆周运动。

在圆周运动中，最常见和最简单的是匀速圆周运动，下面我们主要研究匀速圆周运动。

质点沿圆周运动，如果在相等的时间里通过的圆弧长度都相等，这种运动就叫做匀速圆周运动。砂轮上每一点的运动，电钟指针上每一点的运动，都可以看作匀速圆周运动。

质点做匀速圆周运动的时候，它通过的弧长Δs跟所用的时间Δt之比是个定值，这个比值就是匀速圆周运动的速率，即速度的大小，

\[v = \frac{{\Delta s}}{{\Delta t}}\]

可以看出，v的数值等于质点在单位时间内通过的弧长。

质点做匀速圆周运动时，运动一周所用的时间叫做周期。

如果质点沿半径为r的圆周做匀速圆周运动，周期是T，那么它的速度的大小可以根据下式求出：

\(v = \frac{{2\pi r}}{T}\)             （1）

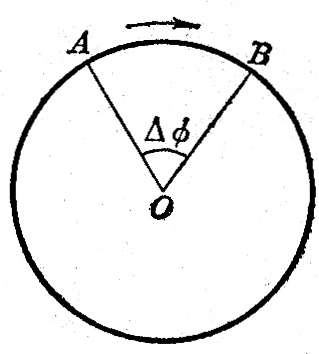
质点做圆周运动的快慢也可以用角速度来描述，如图4-16所示，沿圆周运动的质点，在时间Δt里由A点运动到B点，与此同时，连接质点和圆心的半径OA也绕圆心转过一个角度Δϕ，显然，质点沿圆周运动得越快，在相等的时间里质点通过的圆弧就越长，半径转过的角度也就越大。

在匀速圆周运动的情况下，在任何相等的时间里质点通过的圆弧长度都相等，连接质点和圆心的半径转过的角度也都相等。即半径转过的角度Δϕ跟所用的时间Δt之比是个定值。我们把这个比值叫做匀速圆周运动的角速度，角速度的符号是ω，写成公式就是

\[\omega = \frac{{\Delta \phi }}{{\Delta t}}\]

可以看出，角速度的数值等于在单位时间里半径转过的角度。

角速度的单位是由角度的单位和时间单位决定的。在国际单位制中，角度用弧度作单位，时间用秒作单位，角速度的单位是弧度/秒，读作弧度每秒。

如果质点做匀速圆周运动的周期是T（秒），在时间望里半径转过的角度是2π（弧度），那么

\(\omega = \frac{{2\pi }}{T}\)             （2）

研究匀速圆周运动时，为了跟角速度区别开，习惯上常常把前面讲过的匀速圆周运动的速度叫做线速度。在时间Δt内，如果做匀速圆周运动的质点通过的弧长是Δs，半径r转过的角度是Δϕ（弧度），由于Δs＝r·Δϕ，v＝\(\frac{{\Delta s}}{{\Delta t}}\)＝r\(\frac{{\Delta \phi }}{{\Delta t}}\)，所以线速度的大小跟角速度的关系是

v＝ωr。         （3）

在直线运动中，我们是用速度的概念来描述运动快慢的。但是，在匀速圆周运动中，除了线速度，还可以用角速度和周期来描述运动的快慢。线速度、角速度、周期既然都是描述匀速圆周运动快慢的物理量，它们之间必然有一定的关系。质点做匀速圆周运动时，圆半径保持不变，周期越小，它运动一周所用的时间越短，那么，单位时间内半径转过的角度就越大，即角速度就越大，单位时间内质点通过的圆弧也越长，即线速度也越大，式（1）、（2）、（3）表示出了它们之闻的定量关系。

我们前面讲过，曲线运动中速度的方向是时刻改变的，所以曲线运动都是变速运动。同样，质点做匀速圆周运动的时候，速度的大小虽然不变，速度的方向却是时刻改变的，它在某一点的即时速度的方向就在这一点的圆周切线上，既然匀速圆周运动的速度方向时刻在改变，因此它跟一般的曲线运动一样，是一种变速运动。“匀速圆周运动”一词中的“匀速”仅是速率不变的意思。

练习五

（1）对于做匀速圆周运动的物体，下面的哪种说法对，哪种说法不对？①速度不变；②速率不变；⑧角速度不变。

（2）钟表上分针的周期和角速度是多大？

（3）半径10cm的砂轮，每0.2s转一圈，砂轮旋转的角速度是多大？砂轮上离转轴不同距离的点，其角速度是否相等？线速度是否相等？试求离转轴最远处的线速度。

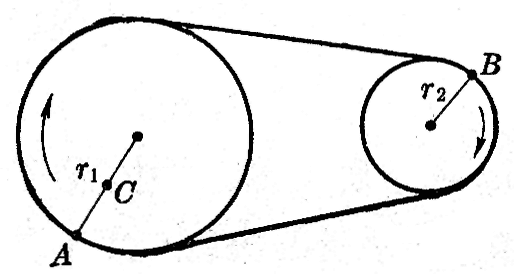
（4）在皮带传动（图4-17）中，两皮带轮轮缘上的线速度是相等的，如果大轮的半径是r₁，小轮的半径是r₂，求大轮和小轮的角速度之比。如果大轮每分钟的转数为n₁，小轮每分钟的转数n₂是多少？

发布时间：2015/7/10 下午8:40:53  阅读次数：1940