二、运动的合成和分解

研究比较复杂的运动时，常常把这个运动看作是两个或几个比较简单的运动组成的，使问题变得容易研究。作为研究曲线运动的准备，我们先讨论一下运动的合成和分解。

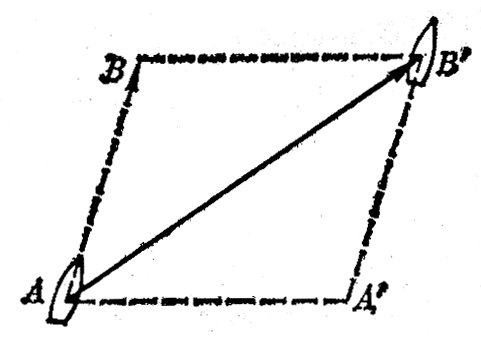
轮船渡河的运动可以看作是由两个运动组成的。假如河水不流动，而轮船在静水中沿AB方向行驶，那么经过一段时间轮船将从A点运动到B点（图4-5）。假如轮船没有开动，而河水流动，那么轮船被河水冲向下游，经过相同一段时间，轮船将从A点运动到Aʹ点。现在轮船在流动的河水中行驶，它同时参与上述两个运动，经过这段时间将从A点运动到Bʹ点。轮船从A点到Bʹ点的运动，就是上述两个分运动的合运动。

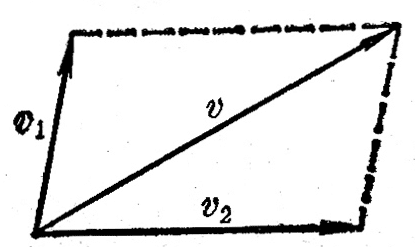
既然一个运动可以看作是由分运动组成的，那么，已知分运动的情况，就可以知道合运动的情况，由于位移是矢量，已知分运动在一段时间内发生的位移，应用平行四边形法则就可以求出合运动的位移。同样，由于速度和加速度都是矢量，已知分运动在某一时刻的速度和加速度，应用平行四边形法则就可以求出合运动在那一时刻的速度和加速度。例如，在上面轮船渡河的例子中，如果知道了轮船在静水中的速度v₁的大小和方向，以及河水流动的速度v₂的大小和方向，应用平行四边形法则，就可以求出轮船合运动的速度v（图4-6）。这种已知分运动求合运动，叫做运动的合成。

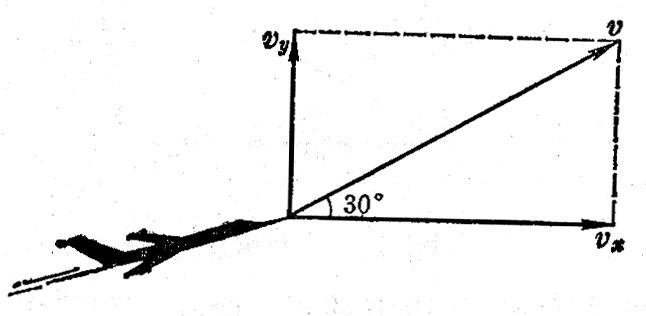
反过来，已知合运动的情况，应用平行四边形法则，也可以求出分运动的情况。例如，飞机以300km/h的速度斜向上飞行，方向与水平面成30°角。我们很容易求出飞机在水平方向和竖直方向的速度。由于飞机斜向上飞行的运动可以看作是它在水平方向和竖直方向两个分运动的合运动，如图4-7把合运动的速度v分解成水平方向和竖直方向的分速度v_x和v_y，它们就是这两个分运动的速度。

v_x＝vcos30°＝260km/h，

v_y＝vsin30°＝150km/h。

这种已知合运动求分运动，叫做运动的分解。

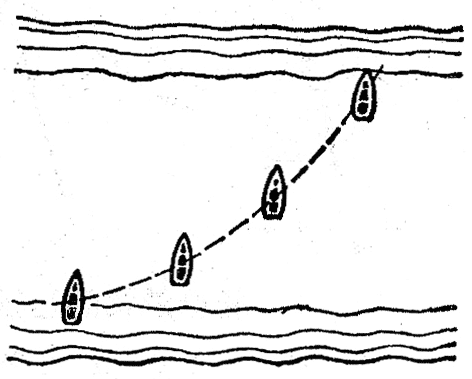
在图4-5轮船渡河的例子中，由于轮船在AB方向是匀速行驶的，河水在AAʹ方向是匀速流动的，轮船的两个分运动的速度矢量都是恒定的，轮船的合运动的速度矢量也是恒定的，所以合运动是匀速直线运动。但一般来说，两个直线运动的合运动，并不一定都是直线运动，在轮船渡河的例子中，如果轮船在AB方向是加速行驶的，河水在AAʹ方向的流动是匀速的，那么轮船的合运动就不是直线运动，而是曲线运动了（图4-8）。

一些常见的曲线运动往往可以分解为两个简单的直线运动，下面我们将用运动的合成和分解来研究几种曲线运动。

练习二

（1）降落伞在下落一定时间以后的运动是匀速的。没风的时候某跳伞员着地的速度是5.6m/s，现在有风，风使他以4.0m/s的速度沿水平方向向东移动，他将以多大的速度着地？这个速度的方向怎样？

（2）炮筒与水平方向成60°角，炮弹从炮口射出时的速度是800m/s。这个速度在竖直方向和水平方向的分速度各是多大？

（3）小汽艇在静水中的速度是12km/h，河水的流速是6.0km/h。如果驾驶员向着垂直于河岸的方向驾驶，小汽艇在河水中实际行驶的速度是多大？方向怎样？

发布时间：2015/7/7 下午9:23:00  阅读次数：836