十一、牛顿运动定律的适用范围

自从十七世纪以来，以牛顿定律为基础的经典力学不断发展，取得了巨大的成就。从研究最简单的质点做直线运动的力学，到研究由若干质点组成的所谓质点系做各种复杂运动的力学，从研究不变形的物体即所谓刚体的力学，到研究可变形的连续介质的力学，如流体力学和弹性力学，都属于经典力学的范围。经典力学在科学研究和生产技术中有广泛的应用，经典力学和天文学相结合，建立了天体力学。经典力学和工程实际相结合，建立了各种应用力学，如水力学、材料力学、结构力学等等。从行星的运动到地面上各种物体的运动；从大气的流动到地壳的变动；从设计各种机械到拦河筑坝、修建桥梁和高楼大厦；从人力车、马车的运动到汽车、火车、飞机等现代交通工具的运动；从抛出石块到发射导弹、人造卫星和航天飞机——所有这些都服从经典力学的规律。经典力学在这样广阔领域内用来解决实际问题时得到的结果与实际情况相符合，证明了牛顿定律的正确性。

但是，牛顿定律和一切物理定律一样，只具有相对的真理性。这就是说，牛顿定律也有它的适用范围。

随着物理学的发展，特别是十九世纪以来电磁理论的发展，不断发现新的事实，如高速运动的电子的质量随着速度的增大而增大。这些事实，用经典力学无法加以说明，经典力学的理论与实验事实之间发生了矛盾。在这种情况下，在二十世纪初，著名的物理学家爱因斯坦（1879～1955）提出了狭义相对论，成为现代物理的开端。狭义相对论从根本上改变了我们通常对空间和时间昀看法，提出了一种新的时空观。从经典力学看来，物体的长度和时间间隔跟物体运动的速度没有关系，相对论却指明了它们跟速度的密切关系。相对论还指出，物体的质量不是固定不变的，它随着物体运动速度的增大而增大。设m₀为物体静止时的质量，那么，物体以速度v运动时，它的质量m可以根据相对论力学的公式计算出来。计算表明，当物体的运动速度移接近于光速c时，运动物体的质量m远大于它的静止质量m₀。例如v＝0.8c时，m≈1.7m₀；v＝0.95c时，m≈3.1m₀。这时，经典力学就不再适用了，当物体的运动速度v远小于光速c时，虽然运动物体的质量m比它的静止质量m₀要大，但相差甚微，可以不予考虑，而认为运动物体的质量没有改变，经典力学仍旧适用。实际上，太阳系里的一切宏观物体，如行星、卫星、人造飞船、地球上的各种交通工具以及我们通常研究的物体，它们的速度都远小于光速，都显示不出质量随速度而改变的现象。例如，地球的公转速度v＝3×10⁴m/s，以这个速度运动的物体，它的质量的改变大约只为静止质量的十万万分之五，这样微小的变化实际上是无法观测出来的。这就是说，对于太阳系里一切宏观物体的运动来说，经典力学已经足够准确了。总之，处理低速运动问题时，经典力学是完全适用的；处理高速运动问题时，必须用相对论力学。经典力学是相对论力学在低速时良好的近似。

经典力学是在研究宏观物体的基础上总结出来的规律。随着生产和科学技术的发展，十九世纪末和二十世纪初以来，人们对物质世界的研究深入到原子内部，发现电子、质子、中子等微观粒子，不仅具有粒子性，而且具有波动性，它们的运动规律一般不能用牛顿运动定律来说明。二十世纪初期，人们建立了量子力学，用来描述微观粒子的规律性，关于量子力学的基本观念，如所谓波粒二象性，到高中三年级再来学习。

经典力学只适用于解决物体的低速运动问题，不能用来处理高速运动问题；经典力学只适用于宏观物体，一般不适用于微观粒子，这就是牛顿定律的适用范围。

复习题

（1）亚里士多德对力和运动的关系是怎样认识的？他的观点有什么错误？

（2）牛顿第一定律的内容是什么？伽利略的理想实验有什么重要意义？

（3）学习了牛顿第一定律之后，你对力的概念有什么进一步的认识？物体运动状态的改变跟什么有关？为什么说质量是物体惯性的量度？

（4）牛顿第二定律的内容是什么？写出它的公式。

（5）运用牛顿运动定律可以解决哪些方面的问题？你已经解过一些动力学的习题，你自己总结一下解题的基本思路和步骤。

（6）质量和重量有什么区别和联系？

（7）什么叫超重？什么叫失重？

（8）单位制在物理计算中有什么作用？

（9）牛顿运动定律的适用范围是什么？

习题

（1）一个小金属车可以和另外两个相同的小木车在天平上平衡。用一个力作用在小金属车上，得到2m/s²的加速度。如果用相同的力作用在一个静止的小木车上，经过2s，小木车的速度是多大？

（2）一个质量是m千克的物体沿着光滑的斜面下滑（不计滑动摩擦），斜面的倾角是θ。试证明这个物体下滑的加速度a＝gsinθ。

（3）一个质量是10g的物体沿着光滑的斜面从静止开始滑下（不计摩擦），开始滑下时的竖直高度是10cm，斜面的倾角是30°，这个物体滑到斜面末端时的速度是多大？另一个质量是20g的物体也沿着光滑的斜面从静止开始滑下，开始滑下时的竖直高度相同，斜面的倾角是45°，这个物体滑到斜面末端时的速度是多大？写出速度移的表达式，并说明物体滑到斜面末端时的速度移只跟开始滑下时竖直高度h、重力加速度g有关，跟物体的质量m、斜面的倾角θ无关。

（4）一个放在水平面上的物体，质量是0.50kg，在水平方向受到6.0N的拉力，得到10m/s²的加速度。求这个物体和平面间的滑动摩擦系数。

（5）质量是2.75t的载重卡车，在2900N的牵引力作用下开上一个山坡，沿山坡每前进1m升高0.05m，卡车由静止开始前进100m时速度达到36km/h。求卡车在前进中所受的摩擦阻力。

（6）汽车开上一段坡路。汽车的质量是1500kg，发动机的牵引力是3000N，摩擦阻力是900N。沿坡路每前进10m升高2m米，坡长282m。汽车用20s走完这段坡路。求上坡前的速度和到达坡顶的速度。

（7）有一个质量是3.0kg的木块以速度v₀沿光滑的水平面移动。一个与v₀方向相反的18N的力作用在木块上，经过一段时间，木块的速度减小到原有速度v₀的一半，木块移动了9.0m的路程，这段时间有多长？v₀是多大？

（8）一个物体在两个彼此平衡的力作用下处于静止状态。现在把其中某一个力逐渐减小到零，这个物体的加速度和速度的绝对值怎样变化？如果再逐渐把这个力恢复，这个物体的加速度和速度的绝对值又将怎样变化？

（9）一个放在水平面上的质量是5.0kg的物体，受到与水平方向成30°角的斜向上方的拉力作用，物体产生沿水平方向的加速度是2m/s²。物体跟平面的滑动摩擦系数是0.1。求拉力是多大？

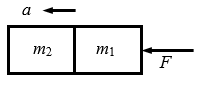
（10）1966年曾在地球的上空完成了以牛顿第二定律为基础的测定质量的实验。实验时，用双子星号宇宙飞船m₁去接触正在轨道上运行的火箭组m₂，接触以后，开动飞船尾部的推进器，使飞船和火箭组共同加速（图3-15）。推进器的平均推力F等于895N，推进器开动7.0s，测出飞船和火箭组的速度改变是0.91m/s。已知双子星号宇宙飞船的质量m₁＝3400kg。求火箭组的质量m₂是多大。

解：推进器的推力使宇宙飞船和火箭组产生的加速度

a＝\(\frac{{0.91}}{{7.0}}\)m/s²＝0.13m/s²。

根据牛顿第二定律得

F＝ma＝（m₁＋m₂）a，

所以

m₂＝\(\frac{F}{m}\)－m₁＝（\(\frac{895}{0.13}\)－3400）kg＝3500kg。

实际上，火箭组的质量已经被独立地测出。实验的目的是要发展一种技术，找出轨道中另一个国家的人造卫星的未知质量。事先已测出火箭组的质量为3660kg，因而实验误差在5%以内——正好在预期的误差范围之内。

（11）文艺复兴时代意大利的著名画家和学者达·芬奇提出了如下的原理：

如果力F在时间t内使质量是m的物体移动一段距离s，那么：

相同的力在相同的时间内使质量是一半的物体移动2s的距离；

②或者相同的力在一半的时间内使质量是一半的物体移动相同的距离；

③或者相同的力在两倍的时间内使质量是两倍的物体移动相同的距离；

④或者一半的力在相同的时间内使质量是一半的物体移动相同的距离；

⑤或者一半的力在相同的时间内使质量相同的物体移动一半的距离。

这些原理正确不正确？为什么？

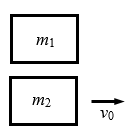
（12）有两个物体，质量为m₁和m₂，m₁原来静止，m₂以速度v₀向右运动（图3-16）。它们同时开始受到大小相等、方向与v₀相同的恒力F的作用，它们能不能在某一时刻达到相同的速度？分m₁＜m₂，m₁＝m₂，m₁＞m₂三种情况来讨论。

发布时间：2015/7/6 下午10:02:44  阅读次数：1340