九、牛顿运动定律的应用（二）

上一节讲了，已知物体的受力情况，可以确定物体的运动情况。与此相反，如果已知物体的运动情况，根据运动学公式求出物体的加速度，也可以根据牛顿第二定律确定物体所受的外力。这是力学所要解决的又一方面的问题。

【例题1】1000t的列车由车站出发做匀变速运动，列车经过100s通过1000m的路程。求机车的牵引力，已知运动阻力是车重的0.005倍。

在这道题目里物体的运动情况是已知的：列车做初速度为零的匀变速运动，100s钟通过了1000m的路程，即位移为1000m。取列车前进的方向为正方向，列车的加速度可以用公式s＝\(\frac{1}{2}\)at²求出，即

a＝\(\frac{{2s}}{{{t^2}}}\)＝\(\frac{{2 \times 1000}}{{{{100}^2}}}\)m/s²＝0.20m/s²。

列车在水平方向受两个力的作用：牵引力F和阻力f。已知阻力的大小f＝10⁶×9.8×5×10^-3N＝4.9×10⁴N。根据牛顿第二定律F_合＝F－f＝ma就可以求出见

F＝f＋ma

＝（4.9×10⁴＋100×0.20）N

＝2.5×10⁵N。

F为正值表示牵引力方向和所取正方向即列车前进的方向相同。

【例题2】在汽车中的悬线上挂一个小球，实验表明，当汽车做匀变速运动时，悬线将不在竖直方向，而与竖直方向成某一固定角度（图3-10）。已知小球的质量是30g，汽车的加速度为5.0m/s²，求悬线对小球的拉力。

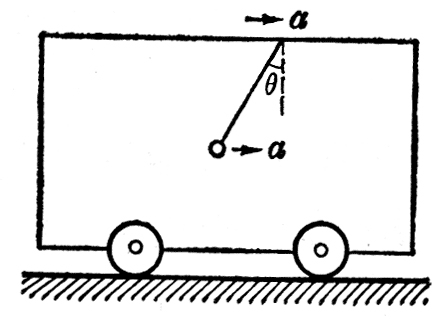
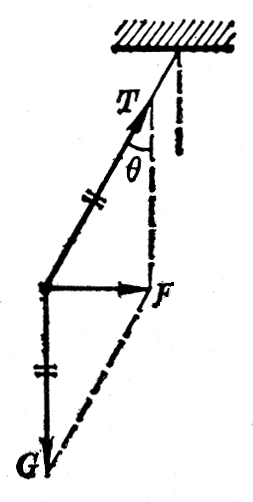
在解这个问题时，我们以小球为研究对象，它的运动情况是已知的，因为小球随着汽车一起做匀变速运动，所以汽车的加速度a就是小球的加速度。小球的受力情况是：受重力G和绳的拉力T的作用，小球的受力图如图3-11所示。小球除了受到这两个力以外，周围再也没有别的物体对小球施加什么力了。小球的加速度a正是由于G和T这两个力的合力F引起的，根据牛顿第二定律知道，这个合力的方向一定与小球加速度的方向相同，而且F＝ma，已知合力F，又知道一个分力G＝mg，利用平行四边形法则不难求出另一个分力T：

T²＝F²＋G²＝（ma）² ＋（mg）²，

\[\begin{array}{l}T = m\sqrt {{a^2} + {g^2}} \\ = 0.030\sqrt {{{5.0}^2} + {{9.8}^2}} {\rm{N}}\\ = 0.33{\rm{N}}\end{array}\]

拉力T的方向可以用悬线与竖直方向的角度θ表示出来，角θ不难用tanθ＝\(\frac{{ma}}{{mg}}\)＝\(\frac{{a}}{{g}}\)求出，请同学们自己算出这个角度。

在一些实际问题中，常常需要根据牛顿第二定律从物体的运动情况来确定力。例如，运动物体所受的线的拉力和支持物的支持力通常很难用实验来测定，但是，如果知道了物体的运动情况，算出加速度，根据牛顿第二定律就可以把拉力和支持力作为未知力求出来。

在动力学问题中，如果知道物体的受力情况和加速度，也可以测出物体的质量。这就是说，质量可以用动力学的方法来测定，本章习题中的第10题，就是用动力学方法测定质量的一个有趣的题目，希望同学们好好研究一下那个题目。

从上面两节的例题可以看出，应用牛顿第二定律和运动学的公式解题时，要首先确定作为研究对象的物体，然后分析它的受力情况和运动情况，再应用牛顿第二定律和适当的运动学公式求出未知量。这里，正确分析物体受力情况和运动情况是解题的关键。

练习八

（1）质量是20t的车厢以0.2m/s²的加速度前进，运动的阻力是它的重量的0.02倍，牵引力是多少牛？

（2）列车在水平铁路上行驶，在50s内速度由32km/h增加到54km/h，列车的质量是1.0×10³t，机车对列车的牵引力是1.5×10⁵N。求列车在运动中所受的阻力。

（3）以15m/s行驶的无轨电车，在关闭电动机以后经过10s停下来。电车的质量是4.0×10³kg。求电车所受的阻力。

（4）用弹簧秤拉着一个物体在水平面上做匀速运动，弹簧秤的读数是0.40N。然后用弹簧秤拉着这个物体在这个水平面上做匀变速运动，测得加速度是0.85m/s²，弹簧秤的读数是2.10N。这个物体的质量是多大？

发布时间：2015/7/6 下午9:09:30  阅读次数：606