十二、竖直上抛运动

将物体用一定的初速度沿竖直方向向上抛出去，物体所做的运动叫做竖直上抛运动。竖直上抛的物体，在上升过程中，速度越来越小，加速度的方向跟速度的方向相反，是竖直向下的；当速度减小到零的时候，物体上升到最大高度。然后物体从这个高度自由下落，速度越来越大，加速度的方向跟速度的方向相同，也是竖直向下的。如果不考虑空气的阻力，这两个过程的加速度都是重力加速度g。因此，在处理竖直上抛运动的问题时，可以分两步进行计算：上升过程用初速度不为零的匀变速直线运动公式来计算，下降过程用自由落体公式来计算。

由于上升运动和下降运动的加速度矢量是相同的，我们也可以把竖直上抛运动看做是一个统一的匀变速直线运动，而上升运动和下降运动不过是这个统一的运动的两个过程。这样，我们就可以用匀变速运动的速度公式和位移公式来统一讨论竖直上抛运动。在讨论这类问题中，我们习惯上总是取竖直向上的方向作为正方向，重力加速度g总是取绝对值。这样，竖直上抛运动的速度公式和位移公式通常就写做

v₁＝v₀－gt，

s＝v₀t－\(\frac{1}{2}\)gt²。

注意：上述公式中的t是从抛出时刻开始计时的，s是运动物体对抛出点的位移。

现在我们应用上述公式讨论几个具体问题。

（1）物体上升的时间

设物体经过时间t₁上升到最高点，在这一时刻，物体是静止的，由此可得

v₀－gt₁＝0，

所以物体上升的时间

t₁＝\(\frac{{{v_0}}}{g}\)。

（2）上升的最大高度

物体上升的最大高度，就是t＝t₁＝\(\frac{{{v_0}}}{g}\)时的高度。把这个式子代入位移公式就可以得出物体上升的最大高度H：

H＝v₀t₁－\(\frac{1}{2}\)gt₁²＝\(\frac{{v_0^2}}{{2g}}\)。

（3）物体下落的时间

物体落回到初位置时位移为零，即s＝0。代入位移公式得

v₀t－\(\frac{1}{2}\)gt²＝0，

t（v₀－\(\frac{1}{2}\)gt）＝0。

所以

t＝0，t＝\(\frac{{2{v_0}}}{g}\)。

t＝0表示物体运动开始时的时刻，t＝\(\frac{{2{v_0}}}{g}\)表示物体经过上升和下降过程后落回原地所需的时间。如果物体下降过程的时间为t₂，那么t＝t₁＋t₂，所以

t₂＝t－t₁＝\(\frac{{2{v_0}}}{g}\)－\(\frac{{{v_0}}}{g}\)＝\(\frac{{{v_0}}}{g}\)。

比较t₁和t₂可知，t₁＝t₂，即物体上升到最大高度所用的时间跟物体从这个高度落回原地所用的时间相等。

（4）落地速度

已知落地时间为t＝\(\frac{{2{v_0}}}{g}\)，由公式v_t＝v₀－gt可以求出落回原地的速度为

v_t＝v₀－g·\(\frac{{2{v_0}}}{g}\)＝－v₀。

可见，物体落回原地的速度跟抛出的初速度大小相等，方向相反。

实际上，在竖直上抛运动中，不但上升时间等于下落时间，而且在上升过程中通过某一位置的速度和下落过程中通过这个位置的速度总是大小相等、方向相反的。有兴趣的同学，对于后一论断可以自己试做证明。

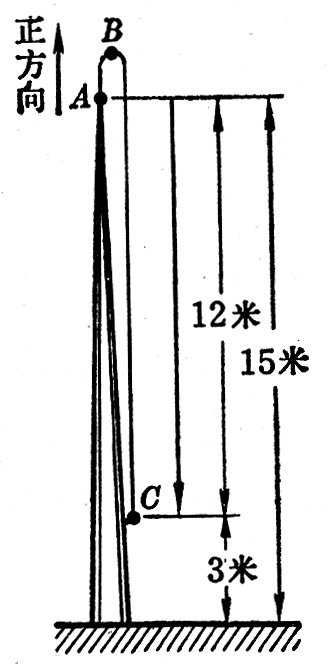
【例题】在15m高的塔上以4m/s的初速度竖直上抛一个石子（图2-22），求经过2s后石子离地面的高度。取g＝10m/s²。

用位移公式来计算：

s＝v₀t－\(\frac{1}{2}\)gt²

＝（4×2－\(\frac{1}{2}\)×10×2²）m

＝－12m。

这表示经过2s后石子对抛出点的位移的大小是12m，方向是竖直向下的，即石子经过2s后在塔顶下方12m处，因而离地面的高度是15m－12m＝3m。

这个例题同学们也可以分上升运动和下降运动两步来计算，所得结果是相同的。显然，这样分步计算比较麻烦。

练习十一

（1）在竖直上抛运动中，v_t与v₀何时方向相同，何时相反？v_t与a何时方向相同，何时相反？

（2）竖直向上射出的箭，初速度是35m/s，上升的最大高度是多大？从射出到落回原地一共用多长时间？落回原地的速度是多大？

（3）竖直上抛的物体，初速度是30m/s，经过2.0s、3.0s、4.0s，物体的位移分别是多大？通过的路程分别是多长？各秒末的速度分别是多大？

（4）在课文的例题中，求经过1s后石子离地面的高度以及石子这时的速度，先分上升运动和下降运动两步来计算，再用统一的公式来计算，并加以比较。

复习题

（1）什么是参照物？在研究物体的运动时为什么一定要选择参照物？

在什么情况下可以把物体看成质点？在什么情况下不能把物体看成质点？

（2）什么是位移？位移和路程有什么区别？在什么情况下位移的大小等于路程？

（3）什么是匀速直线运动？什么是匀速直线运动的速度？匀速直线运动的位移公式是怎样的？利用位移公式，知道物体的初位置，又知道速度，能不能确定物体在任一时刻的位置？

（4）什么是变速直线运动？什么是变速直线运动的平均速度？什么是变速直线运动的即时速度？为什么测量平均速度的时间间隔足够短时，得出的平均速度就可以看做是即时速度？

（5）什么是匀变速直线运动？什么是匀变速直线运动的加速度？速度和加速度的区别是什么？

（6）匀变速直线运动的速度公式和位移公式是什么？利用这两个公式，知道物体的初位置和初速度，又知道加速度，能不能确定物体在任一时刻的位置和速度？

匀变速直线运动的两个有用的推论是什么？

（7）自由落体运动的加速度g有多大？怎样求出自由落体的下落速度和下落距离？

（8）巳知竖直上抛物体的上抛速度v₀，怎样求出它的速度和位移？竖直上抛运动可以分上升运动和下降运动两步来计算，也可以用统一的公式来计算，哪种办法比较简便。

（9）匀速直线运动的位移图象是一条什么样的图线？怎样从这个图象求出物体的速度？

匀速直线运动的速度图象是一条什么样的图线？怎样从这个图象求出物体的位移？

匀变速直线运动的速度图象是一条什么样的图线？怎样从这个图象求出物体的位移？

习题

（1）物体的加速度为零时，它的速度是否一定为零？物体的速度为零时，它的加速度是否一定为零？各举一个例子。

（2）汽车以25km/h的速度行驶了2h，距目的地还有一半路程。要想在40min内到达目的地，在后一半路程中汽车应该以多大速度行驶？

（3）矿井里的升降机，从静止开始加速上升，经过3s速度达到3m/s。然后以这个速度匀速上升25s。最后减速上升，经过2s到达井口时，正好停下来，求矿井深度。

（4）一架飞机以7.0m/s²的加速度做匀加速飞行，计算它的速度由240km/h增加到600km/h所发生的位移和所用的时间。

（5）火车制动后经过20s停下来，在这段时间内前进120m，求火车开始制动时的速度和火车的加速度。

（6）汽车从静止开始做匀变速运动，通过一段距离，速度达到14m/s。汽车通过这段距离的一半时，速度是多大？

（7）一个物体从塔顶上下落，在到达地面前最后一秒内通过的位移是整个位移的9/25。求塔高。

（8）自由落下的物体在某一点速度是20m/s，在另一点的速度是40m/s。求这两点间的距离和经过这段距离所用的时间。

（9）一个竖直上抛的物体，经过4.0s落回原地。经过1.0s，2.0s，3.0s，物体的速度分别是多大？物体的位移分别是多大？通过的路程分别是多长？

（10）气球以10m/s的速度匀速竖直上升，从气球上掉下一个物体，经17s到达地面，求物体刚脱离气球时气球的高度。

（11）初速度为零的匀变速运动，在第1s内、第2s内、第3s内……的位移分别是s_Ⅰ，s_Ⅱ，s_Ⅲ……。试证明：s_Ⅰ，s_Ⅱ，s_Ⅲ……之比等于从1开始的连续奇数之比，即

s_Ⅰ∶s_Ⅱ∶s_Ⅲ……＝1∶3∶5……。

提示：设物体在1s内、2s内、3s内……发生的位移是s₁，s₂，s₃……那么，s_Ⅰ＝s₁，s_Ⅱ＝s₂－s₁，s_Ⅲ＝s₃－s₂……。

（12）从楼顶上落下一个铅球，通过1m高的窗子用了0.1s的时间。楼顶比窗台高多少米？

发布时间：2015/7/1 下午6:15:34  阅读次数：5852