九、匀变速直线运动的位移

匀变速运动的位移又是怎样随着时间而改变的呢？前面已经讲过，匀速运动的位移可以用它的速度图线和横轴之间的面积求出来，应用这种方法也可以求出做匀变速运动的物体的位移。

图2-19中的直线AP是一个做匀变速运动物体的速度图线，为了求出物体在时间t内的位移，我们把时间t划分为许多小的时间间隔，设想物体在每一时间间隔内都做匀速运动，而从一个时间间隔到下一个时间间隔，物体的速度跳跃性的突然增加。因此，它的速度图线，由图2-19甲中一些平行于横轴的间断线段AAʹ，BBʹ，CCʹ，……组成。我们知道，匀速运动的位移可以用速度图线和横轴之间的矩形面积来表示，因此上面设想的物体运动在时间t内的位移，其数值等于图中阶梯状折线AA'BB'CCʹ……下面画有斜线部分的面积。如果时间的分割再细一些（图2-19乙），物体速度的跃变发生得更频繁，它的速度图象就更接近于汽车的真实运动的图象，阶梯状折线和横轴间画有斜线部分的面积数值，就更接近于物体的实际位移，这样不断细分下去，当时间间隔分得足够小时，或者用数学语言来说，当时间间隔无限细分时，间断的阶梯线段就趋近于物体的速度图线；阶梯形折线跟横轴之间的面积，也就趋近于速度图线跟横轴之间的面积。这样我们就得出结论：匀变速运动的位移可以用速度图线和横轴之间的面积来表示。这个结论，不仅对匀变速运动，对一般的变速运动也是适用的。

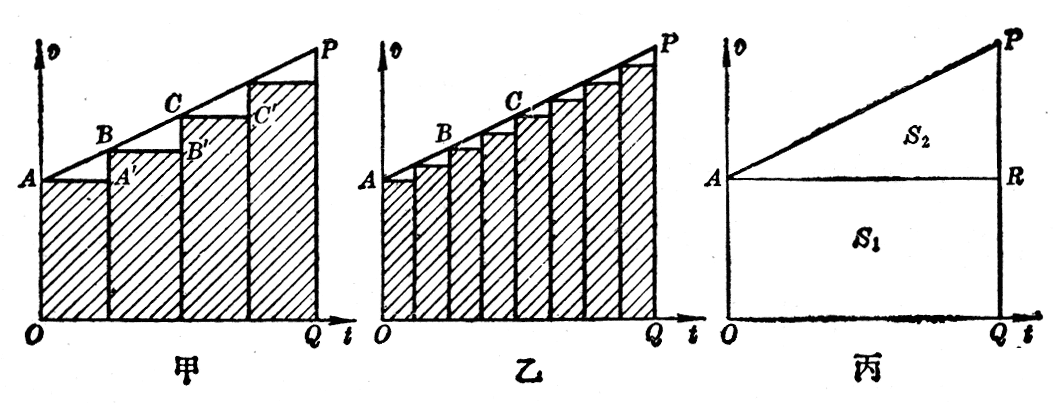
由上述讨论可知，所求的匀变速运动的物体在时间t内的位移，等于图2-19丙中的梯形OAPQ的面积S。从图中可以看出，梯形的面积S等于矩形OARQ的面积S₁和直角三角形APR的面积S₂之和：

S＝S₁＋S₂。

而

S₁＝OA×OQ＝v₀t，

S₂＝\(\frac{1}{2}\)AR×RP＝\(\frac{1}{2}\)at²。

由此可得运动物体在时间t内的位移为

\[s = {v_0}t + \frac{1}{2}a{t^2}\]

这个公式叫做匀变速直线运动的位移公式。它表示出匀变速运动的位移和时间的关系，根据这个公式，如果已经知道物体的初速度和加速度，就可以求出物体在任何时间内发生的位移，从而可以确定物体在任一时刻的位置。

如果匀变速运动的初速度为零，即v₀＝0，上式就简化成下式：

\[s = \frac{1}{2}a{t^2}\]

【例题】以18m/s的速度行驶的汽车，制动后在3.0s内前进36m，求汽车的加速度。

在这个问题里，初速度v₀、行驶时间t和行驶的距离s都是已知的，只要从匀变速运动的位移公式中解出a，就可以求出汽车制动时的加速度。

由公式\(s = {v_0}t + \frac{1}{2}a{t^2}\)得

\[a = \frac{{2(s - {v_0}t)}}{{{t^2}}} = \frac{{2(36 - 18 \times 3)}}{{{3^2}}} = - 4.0{\rm{m/}}{{\rm{s}}^{\rm{2}}}\]

汽车的加速度为－4.0m/s²，负号表明制动产生的加速度的方向与速度的方向相反。

练习八

（1）钢球在斜槽上做初速度为零的匀变速运动，开始运动后0.2s内通过的路程是3.0cm，1s内通过的路程是多少？如果斜面长1.5m，钢球由斜面顶端滚到底端需要多长时间？

（2）飞机着陆后做匀变速运动，速度逐渐减小。已知初速度是60m/s，加速度的大小是6.0m/s²，求飞机着陆后5.0s内通过的路程。

（3）一辆汽车原来匀速行驶，然后以1.0m/s²的加速度加快行驶，经12s行驶了180m，汽车开始加速时的速度是多大？

（4）骑自行车的人以5.0m/s的初速度登上斜坡，得到－40cm/s²的加速度，经过10s，在斜坡上通过多长的距离？

（5）汽车以36km/h的速度行驶。刹车后得到的加速度的大小为4m/s²。从刹车开始，经过3s，汽车通过的距离是多少？

发布时间：2015/6/30 上午7:31:24  阅读次数：994