八、匀变速直线运动的速度

匀变速运动的速度     做匀速运动的物体，在相等的时间里发生的位移都相等，如果知道了位移和时间的比值，即知道了速度，就可以确定位移和时间的关系；如果还知道初位置，就可以知道任一时刻的位置。跟这类似，在匀变速运动中，在相等的时间里速度的变化都相等，如果知道了速度的变化和时间的比值，即知道了加速度，就可以确定速度的变化和时间的关系；如果还知道初速度，就可以知道任一时刻的速度。

前一节里讲过，匀变速运动的加速度公式是

\[a = \frac{{{v_t} - {v_0}}}{t}\]

把这个公式变形，就得到匀变速直线运动的速度公式

\[{v_t} = {v_0} + at\]

这个公式表示出匀变速运动的即时速度是怎样随着时间而变化的。根据这个公式，如果已经知道做匀变速运动的物体的初速度和加速度，就可以求出物体在任一时刻的即时速度。

如果匀变速运动的初速度为零，即v₀＝0，上式就简化成下式：

\[{v_t} = at\]

【例题】汽车紧急刹车后加速度的大小是6.5m/s²，如果必须在2.0s内停下来，汽车行驶的最大允许速度是多少千米/小时？

汽车必须在2.0s内停下来，这就要求它最迟在2s末速度变为零，即v_t＝0。加速度a和运动的时间都是已知的，只要求出初速度v₀，就得到汽车的最大允许速度。

汽车在刹车时，速度越来越小，加速度的方向和速度的方向相反，取速度的方向为正方向，则加速度为负值，即a＝－6.5m/s²。

由公式v_t＝v₀＋at解出v₀，再把已知量代入得

v₀＝v_t－at

＝0－（－6.5）×2.0m/s

＝13m/s＝47km/h。

也就是说，汽车的最大允许速度是47km/h。

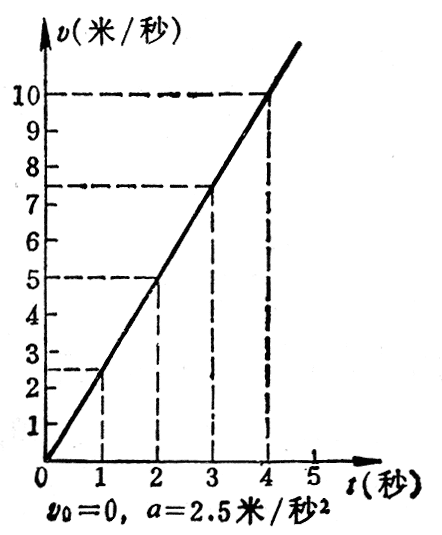
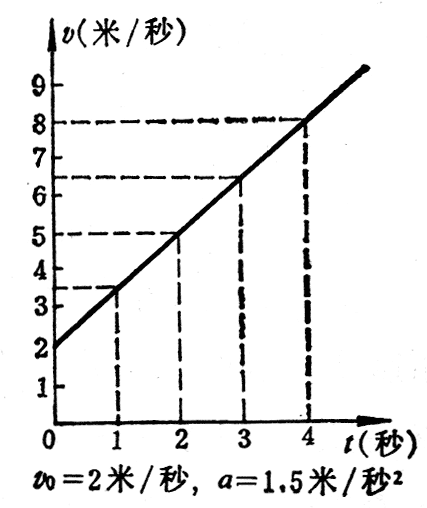
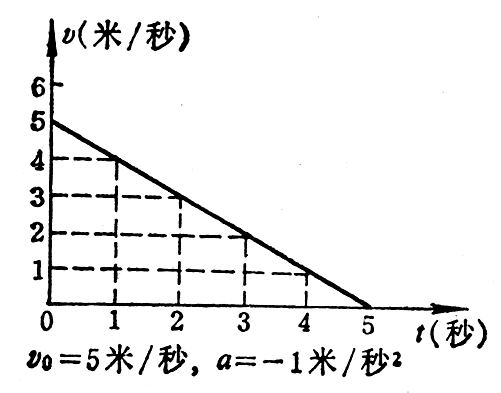
匀变速运动的速度图象     匀变速运动的速度和时间的关系，也可以用图象来表示。由于v_t＝v₀＋at是时间t的一次函数，所以匀变速运动的速度-时间图象（简称为速度图象）是一条直线。图2-15是初速度为零的匀变速运动的速度图象，图2-16是初速度不为零而加速度为正值的匀变速运动的速度图象，图2-17是初速度不为零而加速度为负值的匀变速运动的速度图象，从匀变速运动的速度图象可以求出任意时刻物体的速度，例如从图2-15可以求出4s末的速度是10m/s。从匀变速运动的速度图象也可以求出物体达到某一速度所需的时间。例如从图2-16可以求出速度达到8m/s所需的时间是4s。

>

>

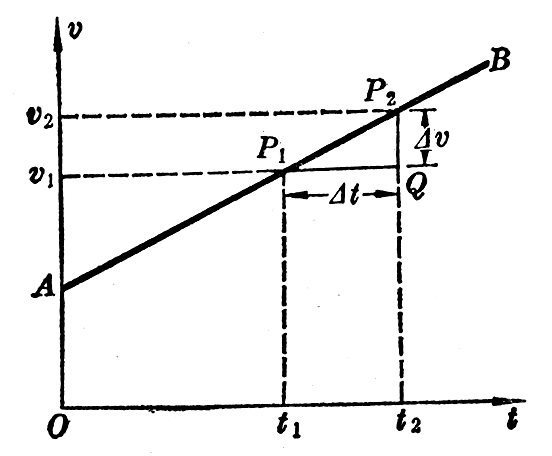
从匀变速运动的速度图象还可以求出加速度，在图2-18所示的速度图象中，用Δt表示t₂－t₁，用Δv表示v₂－v₁，直线AB的斜率k为

\[k = \frac{{\Delta v}}{{\Delta t}} = a\]

这就是说，匀变速直线运动的速度图线的斜率，等于运动物体的加速度，在图2-15和图2-16中，Δv＝v₂－v₁＞0，斜率k为正值，表示加速度为正值。在图2-17中，Δv＝v₂－v₁＜0，斜率k为负值，表示加速度为负值。在同一个坐标平面上，斜率的绝对值越大，即直线越陡，表示加速度的绝对值越大。

练习七

（1）机车原来的速度是36km/h，在一段下坡路上加速度为0.20m/s²。机车行驶到下坡末端，速度增加到54km/h。求机车通过这段下坡路所用的时间。

（2）一辆做匀变速运动的汽车，初速度是34km/h，4.0s末速度变为42km/h。如果保持加速度不变，6.0s末、7.0s秒末的速度是多大？

（3）匀变速运动的加速度是－4.0m/s²。在某一时刻，速度为20m/s。试求这一时刻后4.0s末和5.0s末的速度。

发布时间：2015/6/30 上午7:23:39  阅读次数：1031