六、变速直线运动 平均速度 即时速度

变速直线运动      我们日常看到的直线运动，往往不是匀速的，飞机起飞的时候，运动越来越快，在相等时间里的位移是不相等的。火车进站的时候，运动越来越慢，在相等时间里的位移也是不相等的。

物体在一条直线上运动，如果在相等时间里的位移不相等，这种运动就叫做变速直线运动，变速直线运动有时简称为变速运动。

平均速度      变速运动的物体在相等的时间里的位移不相等，所以它没有恒定的速度，那么，我们怎样来描述它的快慢呢？粗略的办法是把它看作匀速运动。一列火车，半小时内走了28km，尽管它的运动时快时慢，我们仍然可以设想火车在这半小时内是匀速运动的，这样它的速度就是56km/h。这个56km/h，就悬火车在这半个小时内的平均速度。

在变速直线运动中，运动物体的位移和所用时间的比值，叫做这段时间里的平均速度。如果用\(\bar v\)来表示平均速度，那么

\[\bar v = \frac{s}{t}\]

平均速度的数值跟在哪一段时间内计算平均速度有关。上面讲的那列火车，如果在第一个十分钟走了8km，在第二个十分钟走了9km，在第三个十分钟里走了11km，它在三个十分钟里的平均速度就分别是48km/h，64km/h，66km/h。可见，火车半小时内的平均速度虽然是56km/h，但在每个十分钟里的平均速度却是不同的，它的运动逐步加快。

即时速度      平均速度只能粗略地描述做变速运动的物体的运动情况，要精确地描述变速直线运动，还需要知道物体在每一时刻（或位置）的运动速度。运动物体在某一时刻（或某一位置）的速度，叫做即时速度。

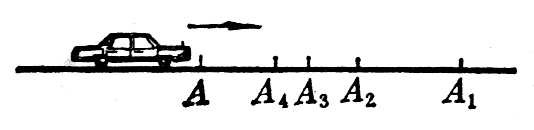
物体在某一时刻或某一位置的速度的意义是什么呢？图2-14表示一辆做变速运动的汽车，我们要确定汽车经过A点时的即时速度。从A起取一小段位移AA₁，求出在这段位移上的平均速度，这个平均速度可以近似地表示汽率经过A点的快慢程度。从A起所取的位移越小，比如依次取位移AA₂、AA₃等，所得的平均速度用来表示汽车经过A点的快慢程度就越精确。当位移足够小时，或者说时间足够短时，所得的平均速度就等于汽车经过A点的即时速度了。

这里所说的“足够短”，应该怎样理解呢？原来，做变速运动的物体的速度总是连续变化的，位移取得越小，或者说时间取得越短，在这段时间内速度的变化就越小。时间足够短时，测量仪器已经分辨不出变速运动和匀速运动的差别，可以认为这一小段时间的运动是匀速的。这时，即使进一步缩短所取的时间，测得的平均速度也不会有什么变化，这个平均速度就等于即时速度。

用数学语言可以更为精确地表达上面所讲的意思。在图2-14中从A起取一小段位移Δs，求出这小段位移内的平均速度\(\frac{{\Delta s}}{{\Delta t}}\)，当Δt趋近于零时，平均速度趋近于某一固定数值——极限值，这个极限值就是汽车经过A点的即时速度。

即时速度既有大小，又有方向，是矢量。在直线运动中，即时速度的方向就是物体经过该点时的运动方向。即时速度的大小叫做即时速率，简称速率，它是一个表示物体运动快慢程度的标量。在某些问题中，如果只需考虑即时速度的大小，可以用速率的概念。

在匀速运动中，知道了速度，根据位移公式就可以确定运动物体在任一时刻的位置。在变速运动中，怎样确定物体在任一时刻的位置和速度呢？

一般地讨论这个问题过于复杂，下面我们只就最简单的变速运动来研究这个问题。

练习五

（1）一辆汽车，起初以30km/h的速度匀速行驶了30km，然后又以60km/h的速度匀速行驶了30km。一位同学认为这辆汽车在这60km中的平均速度是\(\frac{1}{2}\)（30＋60）km/h＝45km/h。这个结果对不对？

（2）骑自行车的人沿着坡路下行，在第1s内通过1m，在笫2s内通过3m，在第3s内通过5m，在第4s内通过7m。求最初两秒内、最后两秒内以及全部运动时间内的平均速度。

（3）在一个速度是v的匀速直线运动中，各段时间内的平均速度以及整个运动的平均速度各是多大？每一时刻的即时速度是多大？

（4）火车以70km/h的速度经过某一路标，子弹以600m/s的速度从枪筒射出。这里指的是什么速度？

发布时间：2015/6/29 下午9:29:27  阅读次数：1021