十二、同一直线上的矢量的运算
本书中常常要处理同一直线上的矢量,这一节我们以力矢量为例讲一讲同一直线上的矢量的运算,以备以后的应用。这里虽然是以力矢量为例来讲的,但对任何矢量都适用。
矢量既有大小,又有方向。如果被运算的矢量在一条直线上,那么,我们就可以用一个带有正负号的数值把矢量的大小和方向都表示出来。为此,我们沿着矢量所在的直线选定一个正方向(图1-33),规定凡是方向跟正方向相同的矢量都取正值,凡是方向跟正方向相反的矢量都取负值,例如图中F1=5N,F2=5N,F3=7N,F4=-5N。这里,根据数值的正负号就可以知道力的方向;而力的大小等于它们的绝对值,分别是5N,5N,7N,5N。

既然同一条直线上的矢量可以用带正负号的数值来表示,它们的运算就可以简化为代数运算。
如果两个矢量大小相等而且方向相同,如图1-33中的F2和F4,我们就说这两个矢量相等,写成代数式就是
F2=F4。 (1)
如果两个矢量大小相等而方向相反,如图1-33中的F1和F2,那么,它们只是符号相反,写成代数式就是
F1=-F2。 (2)
如图1-34所示,设有两个力F1和F2作用在一个物体上,我们可以利用加法运算求出合力F:
F=F1+F2=10N+(-6N)=4N。 (3)
这表示合力的大小是4N,结果是正值表示合力的方向与选定的正方向相同,即合力的方向跟两个力中较大的那个力的方向相同。
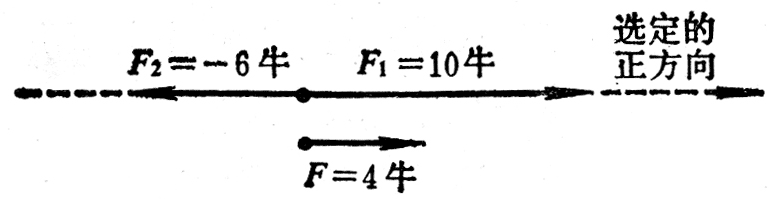
我们也可以利用减法运算求分力。如图1-35所示,已知合力F和一个分力F1,那么,另一个分力F2:
F2=F-F1=8N-(-3N)=11N。 (4)
这表示F2的大小是11N,方向与选定的正方向相同。
需要强调指出的是:只有同一直线上的矢量,它们的运算才可以象上述那样简化成代数运算。这是平行四边形法则在这种特殊情况下的运用。不在同一直线上的矢量,它们的运算不能这样简化成代数运算,仍必须按照平行四边形法则来进行。
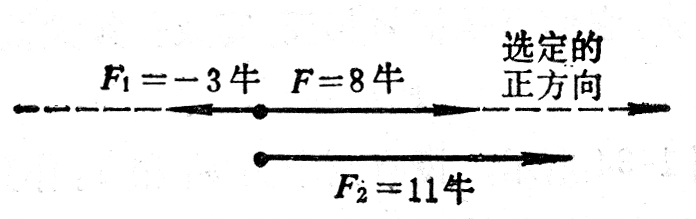
还要指出的是:这里用带有正负号的数值既表示出矢量的大小,又表示出矢量的方向;如果专指矢量的大小,就要取绝对值,即矢量的大小总是正值。本章前面各节中的公式,如公式
f=kx,
f=μN,
\[F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos \theta } ,\]
F=F1+F2(θ=0°),
F=F1-F2(θ=180°),
等等都是关于力矢量大小的公式,利用这些公式来计算,其中的各力都取正值。例如用F=F1-F2来计算图1-34中的合力时,F1=10N,F2=6N,F=F1-F2=4N,这与(3)式所得结果相同。初学时概念上要弄清楚,熟悉起来以后,就可以根据物理思考灵活运用了。
复习题
(1)从力的性质看,力学中经常遇到的有哪几种力?这几种力的情况是怎样的?力可以用哪两种方法来分类?为什么说;拉力、压力和支持力都是弹力?
(2)胡克定律的内容是什么?写出胡克定律的公式。
(3)怎样计算滑动摩擦力的大小?写出它的公式。
(4)牛顿第三定律的内容是什么?为什么说作用力和反作用力不能互相平衡?
(5)力的合成要按照什么法则来进行?这个法则的内容是什么?写出计算合力的大小和方向的公式。
(6)为什么力的分解和合成遵守相同的法则?一个力可以根据什么来分解它?一个力,如果知道它的两个分力的方向,或者知道它的一个分力的大小和方向,那么,这个力的分解有没有确定的答案?
(7)什么叫矢量?什么叫标量?矢量和标量有什么不同?矢量加法要按照什么法则来运算?
(8)你自己总结一下应该怎样分析物体的受力情况。分析时应该注意什么?
习题
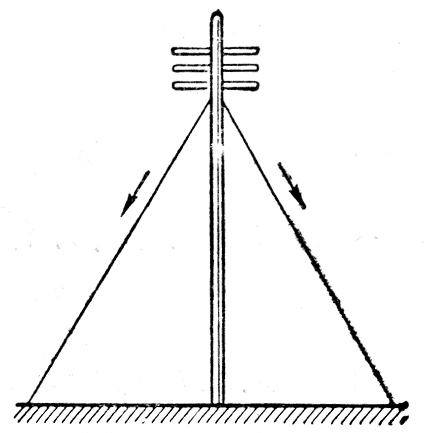
(1)如图1- 36所示,为了防止电线秆倾倒,常在两侧对称地拉上钢绳。如果两条钢绳间的夹角是60°,每条钢绳的拉力都是300N,求两条钢绳作用在电线杆上的合力。
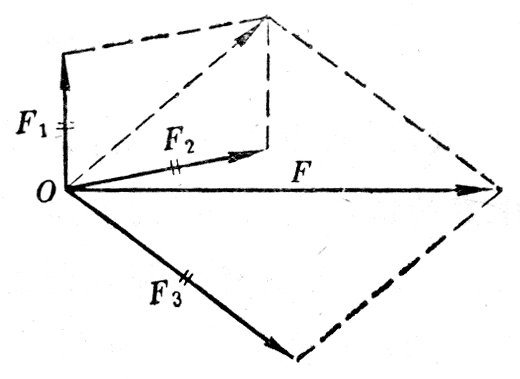
(2)图1-37表示用平行四边形法则求三个共点力F1、F2、F3的合力F。先求出F1和F2的合力,再求出这个合力与F3的合力F。改用三角形法求出这三个力的合力,改变求和的顺序,再分别用平行四边形法则和三角形法求出这三个力的合力。
(3)20N、30N和40N的三个力作用于物体的一点,它们之间的夹角都是120°。求合力的大小和方向。
(4)如图1-38所示,把一个重量为10N的物体挂在绳子上。已知AC=BC=3m,CD=1m。求绳AC和BC所受的拉力。
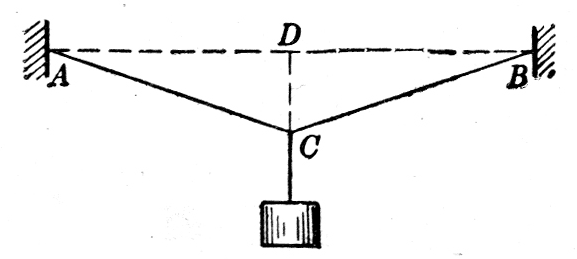
(5)用手握着橡皮绳的两端,在橡皮绳的中间挂一个重物。当两手之间的距离增大或减小的时候,物体对橡皮绳的拉力是否改变?怎样改变?实际做一下,并说明道理。
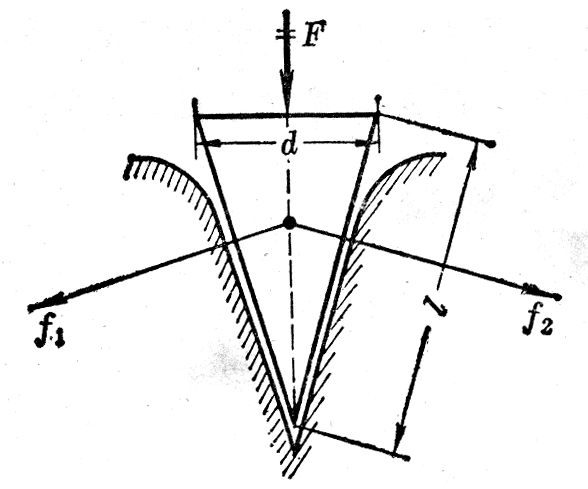
(6)刀、斧、凿、刨等切削工具的刃部叫做劈,劈的纵截面是一个三角形,如图1-39所示。使用劈的时候,在劈背上加力F,这个力产生两个效果,这就是使劈的两个侧面推压物体,把物体劈开。设劈的纵截面是一个等腰三角形,劈背的宽度是d,劈的侧面的长度是l,可以证明:
\[{f_1} = {f_2} = \frac{l}{d}F\]
从上式可知,当F定的时候,劈的两个侧面之间的夹角越小,l/d就越大,f1和f2就越大。这说明了为什么越锋利的切削工具越容易劈开物体。试证明上式。
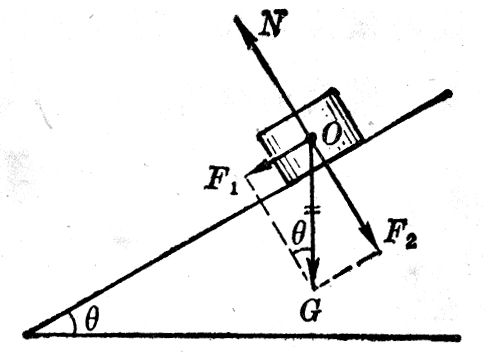
(7)一个物体放在倾角为θ的光滑斜面上,求物体受到的合力。
解:放在斜面上的物体受到两个力的作用:重力G和斜面的支持力N(图1-40)。现在已知N的方向,但不知道N的大小。我们把重力G分解为两个分力:平行于斜面的分力F1=Gsinθ,垂直于斜面的分力F2=Gcosθ。这样,物体相当于受到Gsinθ、Gcosθ和N这三个力的作用。因为物体沿着斜面运动,在垂直于斜面的方向上不发生运动,所以垂直于斜面方向的两个力N和Gcosθ是互相平衡的,它们大小相等,即N=Gcosθ。因此,物体受到的合力的大小为Gsinθ,方向平行于斜面向下。
这里我们先把一个力分解,然后求出合力。这种方法以后我们还会用到。
我们看到,放在光滑斜面上的物体,所受的合力实际上等于重力的一个分力Gsinθ,在这个力的作用下物体将沿着斜面下滑。但是,如果斜面不是光滑的,或者物体还受到别的力,合力将不再等于重力的一个分力Gsinθ。
(8)一个滑雪人沿着山坡滑下。滑雪人的重量是700N,山坡的倾角是30°,滑雪板和雪地的滑动摩擦系数是0.04。求滑雪人所受的合力。
文件下载(已下载 97 次)发布时间:2015/6/25 下午1:41:49 阅读次数:3184
