十、力的分解

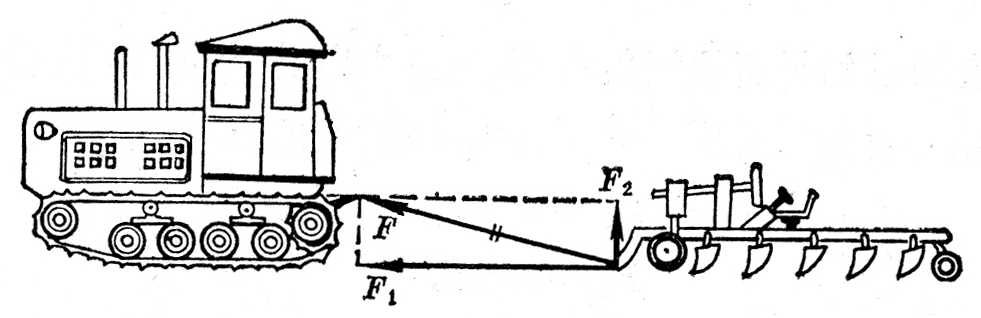
作用在物体上的一个力往往产生几个效果。拖拉机拉犁耕地，对犁的拉力F是斜向上方的，这个力产生两个效果：使犁克服泥土的阻力前进，同时把犁上提，这两个效果相当于两个力产生的（图1-27）：一个水平的力F₁使犁前进，一个竖直向上的力F₂犁上提，可见力F可以用两个力F₁和F₂来代替。几个力，如果它们产生的效果跟原来一个力产生的效果相同，这几个力就叫做原来那个力的分力。求一个已知力的分力叫做力的分解。

因为分力的合力就是原来被分解的那个力，力的分解是力的合成的逆运算，所以一个力分解为两个力同样遵守平行四边形法则，把一个已知力作为平行四边形的对角线，那么与已知力共点的平行四边形的两个邻边就是已知力的两个分力。在图1-27中，F₁和F₂是F的两个分力。

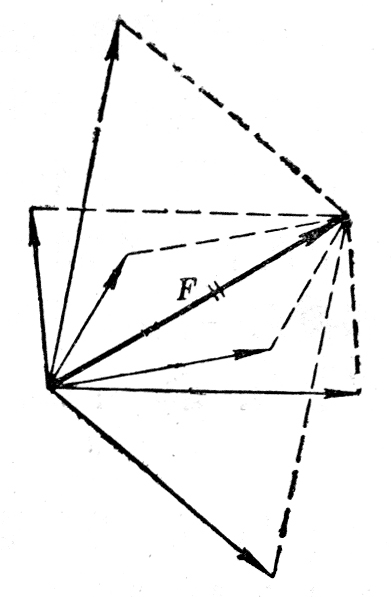
我们知道，如果没有其他限制，对于同一条对角线，可以作出无数个不同的平行四边形（图1-28），也就是说，同一个力F可以分解为无数对大小、方向不同的分力，那么，一个已知力究竟该怎样分解呢？

把一个物体放在斜面上，物体受到竖直向下的重力，但它并不能竖直下落，而要沿着斜面下滑，同时使斜面受到压力。这时重力产生两个效果：使物体沿斜面下滑以及使物体压紧斜面，因此重力G应该分解为这样两个力：平行于斜面使物体下滑的力F₁，垂直于斜面使物体压紧斜面的力F₂（图1-29）。

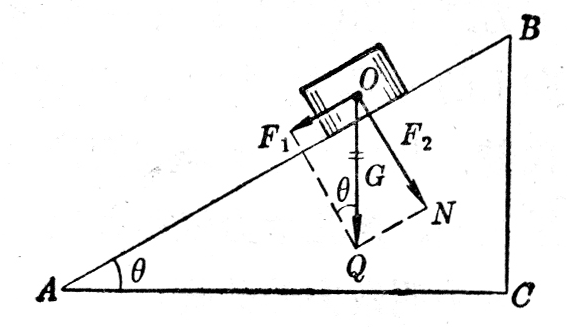
如果已知斜面的倾角θ，就可以求出分力F₁和F₂的大小，由于直角三角形ABC与OQN相似，所以

F₁＝Gsinθ，

F₂＝Gcosθ。

可以看出，F₁和F₂的大小都和斜面的倾角有关。斜面的倾角增大时，F₁增大，F₂减小。车辆上桥时，力F₁阻碍车辆前进；车辆下桥时，力F₁使车辆运动加快，为了行车方便与安全，高大的桥要造很长的引桥，来减小桥面的坡度。

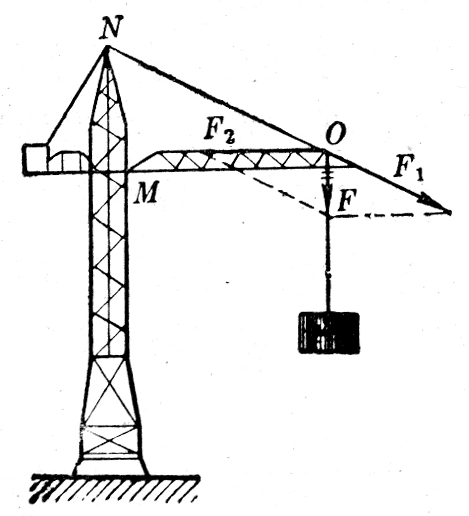
把重量为G的物体挂在图1-30所示的支架上，物体通过绳子使支架上的O点受到一个向下的作用力F，大小等于物体的重量G。力F对支架的两个梁产生的效果是什么呢？如果在M和N处加上小弹簧，可以看到M处的弹簧受到压缩，N处的弹簧受到拉伸。这时力F产生两个效果：沿NO方向拉斜梁，沿OM方向压横粱，因此应该把力F分解为这样两个力：沿NO方向拉斜梁的力F₁，沿OM方向压横梁的力F₂。设斜梁跟墙的夹角为θ，可以看出，

F₁＝F/cosθ，

F₂＝Ftanθ。

从上述例子可以看出，分解一个力要具体考虑这个力产生的效果，一个力我们可以根据它产生的效果来分解它。

练习七

（1）一个物体的重量是20N，把它放在一个斜面上，斜面长AB与斜面高BC之比是5∶3。把重力分解，求出平行于斜面使物体下滑的力和垂直于斜面使物体压紧斜面的力。

（2）图1-31是塔式起重机，钢索NO与水平悬臂MO成30°角，当起重机吊着4.0×10⁴N的货物时，钢索和悬臂分别受多大的力？

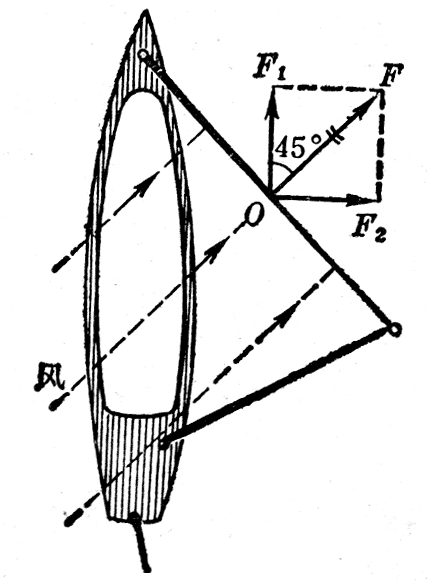
（3）如图1-32所示，垂直作用在帆上的风力F＝1.0×10⁴N。F沿着船身方向的分力F₁使帆船前进，垂直于船身方向的分力F₂使船身侧倾。设F与船身方向成45°角，求力F₁是多大。

（4）把竖直向下的180N的力分解为两个分力，一个分力在水平方向上并等于240N，求另一个分力的大小和方向。

（5）一个小同学跟一个大同学拔河，小同学拉不动大同学。可是用下述办法，小同学就可以拉动大同学。在树干上拴一条绳子，大同学拿着绳子的另一端，沿水平方向把绳子拉紧。小同学用力推绳子的中点，就可以拉动大同学了，实际做一做，并解释所发生的现象。

发布时间：2015/6/24 下午12:24:12  阅读次数：1428