九、力的合成的计算

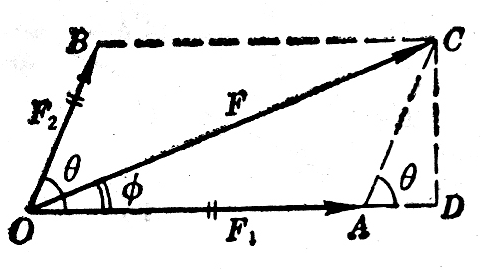
合力的大小和方向，还可以利用公式来计算。图1-24中的OA和OB分别表示两个力F₁和F₂，OC表示它们的合力F，力F₁和F₂的夹角为θ。

在三角形OAC中，根据余弦定理得到

F²＝F₁²＋F₂²－2F₁F₂cos（180°－θ）＝F₁²＋F₂²＋2F₁F₂cosθ。

所以合力的大小

\(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos \theta } \)                    （1）

合力的方向可以用合力跟原来任一个力的夹角表示出来。图中用F跟F₁的夹角φ来表示，利用直角三角形ODC，可以求出角φ的正切：

\(\tan \varphi = \frac{{CD}}{{OD}} = \frac{{CD}}{{OA + AD}} = \frac{{{F_2}\sin \theta }}{{{F_1} + {F_2}\cos \theta }}\)         （2）

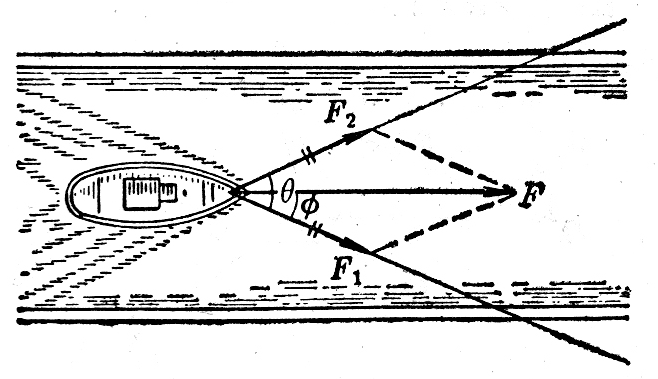
根据（1）（2）两式，可以算出两个共点力的合力的大小和方向。例如在运河两岸拉着一艘货船前进，两条绳对货船的拉力都是2×10³N，两绳互成45°角（图1-25）。合力的大小是：

\[\begin{array}{l} F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos \theta } \\ = \sqrt {{{(2 \times {{10}^3})}^2} + {{(2 \times {{10}^3})}^2} + 2(2 \times {{10}^3})\cos 45^\circ } \\ = 3.7 \times {10^3}N \end{array}\]

\[\begin{array}{l} \tan \varphi = \frac{{{F_2}\sin \theta }}{{{F_1} + {F_2}\cos \theta }}\\ = \frac{{2 \times {{10}^3} \times \sin 45^\circ }}{{2 \times {{10}^3} + 2 \times {{10}^3} \times \cos 45^\circ }}\\ = 0.4142 \end{array}\]

φ＝22°30ʹ。

由于F₁＝F₂，利用力的平行四边形，由几何方法容易证明合力F的方向沿着力F₁和F₂的夹角平分线的方向，这跟应用公式（2）算出夹角φ来表示合力的方向是一致的。

现在我们来讨论，力F₁和F₂的大小一定的时候，合力F的大小跟两个力的夹角θ的关系。

当两个力的方向相同时（图1-26甲），θ＝0°，cos0°＝1，所以F＝F₁＋F₂，合力的大小等于两个力的大小之和，合力的方向跟两个力的方向相同。

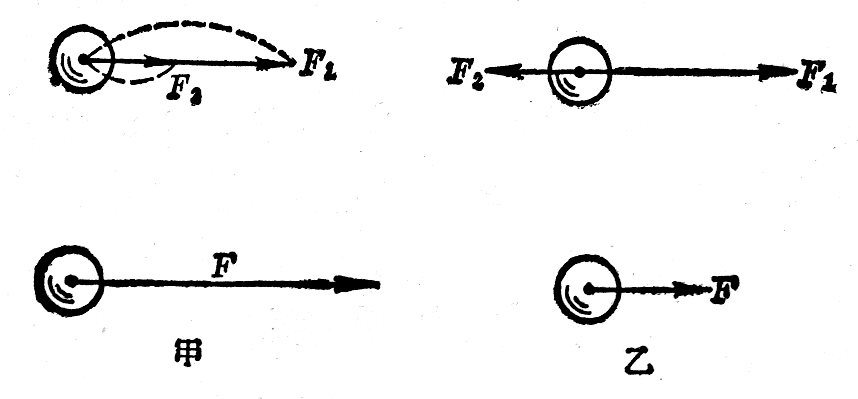
当两个力的方向相反时（图1-26乙），θ＝180°，cos180°＝－1，所以F＝F₁－F₂，合力的大小等于两个力的大小之差，方向跟两个力中较大的那个力的方向相同，如果力F₁和F₂的大小相等，合力就等于零。

当F₁和F₂的夹角θ在0°到180°之间时，θ越大，cosθ的值越小，合力就越小，而且合力的方向也随着夹角θ的变化而变化。

练习六

（1）两个力的合力总大于原来的每一个力，这话对吗？为什么？

（2）有两个力F₁和F₂，用作图法求出当它们之间的夹角θ＝30°，60°，90°，120°，150°，180°时的合力。研究你所作的图，能不能得到结论：夹角θ在0°到180°之间时，θ越大，合力就越小。

（3）两个力的合力什么情况下最大，什么情况下最小？设有两个力，一个是20N，一个是5N。合力的最大值是多大，最小值是多大？

（4）2N和10N的两个力，它们的合力能够等于5N、10N、15N吗？

（5）两个力互成30°角，大小分别是90N和120N。用作图法求出合力的大小和方向，然后再用公式来求。

发布时间：2015/6/23 下午3:03:47  阅读次数：1510