八、力的合成

在大多数实际问题里，物体往往不只受到一个力，而是同时受到几个力，一个物体受到几个力共同作用的时候，我们常常可以求出这样一个力，这个力产生的效果跟原来几个力共同产生的效果相同。一个力，如果它产生的效果跟几个力共同产生的效果相同，这个力就叫做那几个力的合力。求几个力的合力叫做力的合成。

几个力如果都作用在物体的同一点，或者它们的作用线相交于同一点，这几个力叫做共点力。现在我们先来研究作用于物体某一点上的两个力的合成。

图1-22甲表示橡皮条GE在力F₁和F₂的共同作用下，沿着直线GC伸长了EO这样的长度。图1-22乙表示撤去F₁和F₂，用一个力F作用在橡皮条上，使橡皮条沿着相同的直线伸长相同的长度。力F对橡皮条产生的效果跟力F₁和F₂共同产生的效果相同，所以力F是力F₁和F₂的合力。

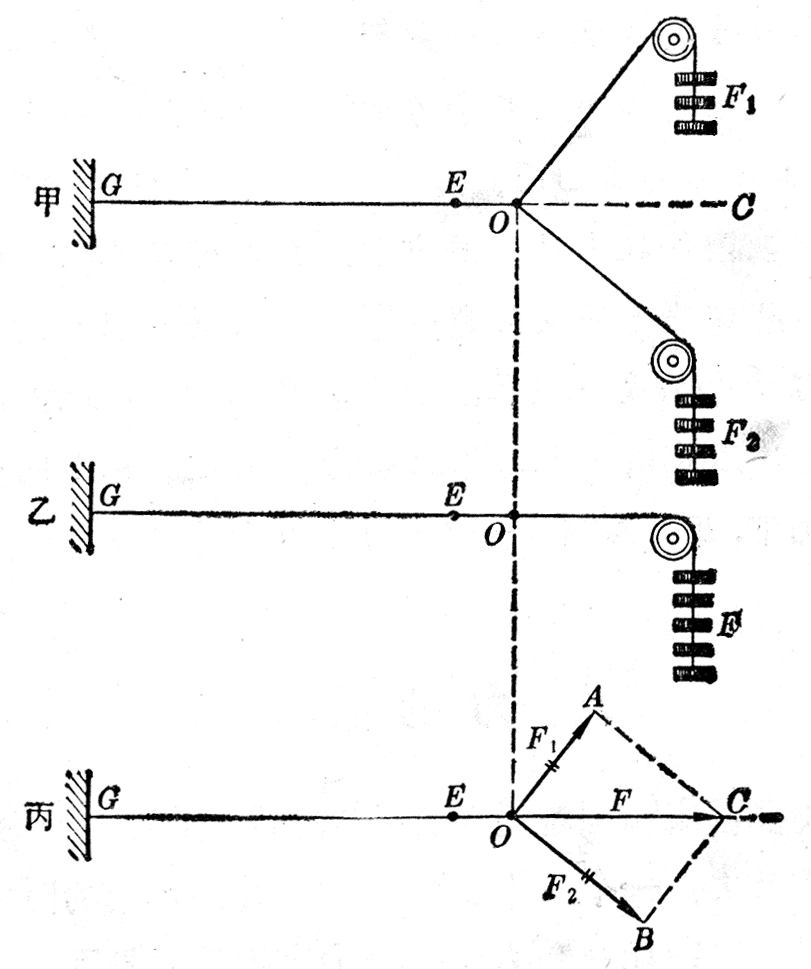
合力F跟力F₁和F₂有什么关系呢？在力F₁和F₂的方向上各作线段OA和OB，根据选定的标度，使它们的长度分别表示力F₁和F₂的大小（图1-22丙）。以OA和OB为邻边作平行四边形OACB。量出这个平行四边形的对角线OC的长度，可以看出，根据同样的标度，合力F的大小和方向可以用对角线OC表示出来。

改变力F₁和F₂的大小和方向，重做上述实验，可以得到同样的结论。

可见，求两个互成角度的共点力的合力，可以用表示这两个力的线段为邻边作平行四边形，这两个邻边之间的对角线就表示合力的大小和方向。这叫做力的平行四边形法则。

根据平行四边形对边平行而且相等的性质，力的平行四边形还可以用更简单的作图法来代替，在图1-23甲中F是共点力F₁和F₂的合力。如图1-23乙所示，从D点出发，把代表F₁和F₂的线段OA、AC首尾相接地画出来，连接O和C，从O指向C的线段就表示合力F的大小和方向，上述作图法叫做三角形法，作三角形OBC（图1-23丙）同样可以求出F₁和F₂的合力F。

如果有两个以上的共点力作用在物体上，我们也可以应用平行四边形法则或三角形法求出它们的合力：先求出任意两个力的合力；再求出这个合力跟第三个力的合力，直到把所有的力都合成进去，最后得到的合力就是这些力的合力。

发布时间：2015/6/23 下午2:47:56  阅读次数：1093