四、胡克定律

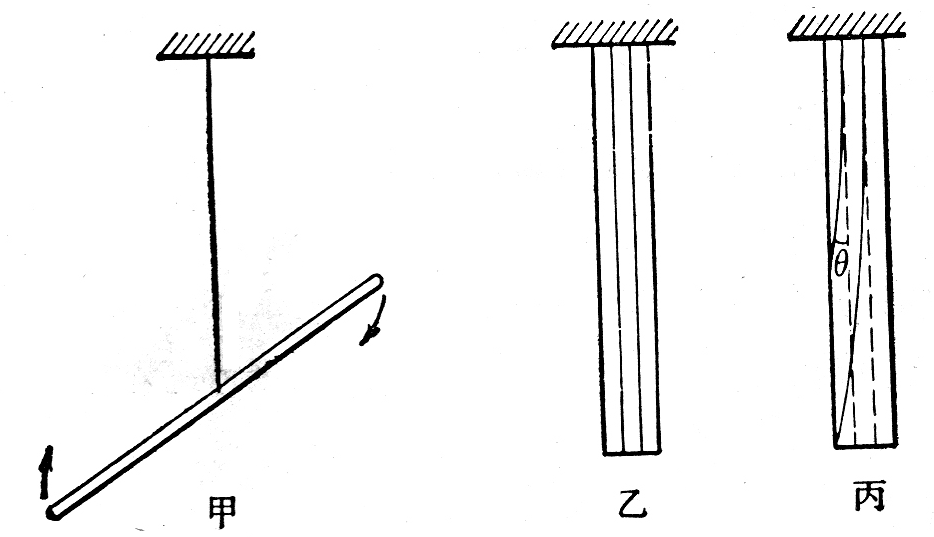
弹力的大小跟形变的大小有关系，形变越大，弹力也越大，形变消失，弹力就随着消失。对于拉伸（或压缩）形变来说，伸长（或缩短）的长度越大，产生的弹力就越大，弹簧伸长或缩短的长度越大，弹力就越大，这是我们从经验中都知道的。把一个物体挂在悬线上，物体越重，把悬线拉得越长（实际上还是看不出来），悬线的拉力也越大．物体发生弯曲时产生的形变叫做弯曲形变。对于弯曲形变来说，弯曲得越厉害，产生的弹力就越大，把弓拉得越满，箭就射出得越远。把一个物体放在支持物上，物体越重，支持物弯曲得越厉害，支持力就越大，还有一种叫做扭转形变，在金属丝的下面挂一个横杆，用力扭这个横杆，金属丝就发生扭转形变（图 1-11）。放开手，发生扭转形变的金属丝产生的弹力会把横杆扭回来。金属丝的扭转角度越大，弹力就越大。

定量地研究各种形变中弹力和形变的关系比较复杂，我们经常遇到的是弹簧的拉伸（或压缩）形变，实验表明：弹簧弹力的大小f和弹簧伸长（或缩短）的长度x成正比。写成公式就是

\[f = kx\]

其中k是比例常数，叫做弹簧的倔强系数，倔强系数是一个有单位的量。在国际单位制中，f 的单位是 N，x 的单位是 m，k 的单位是 N/m。倔强系数在数值上等于弹簧伸长（或缩短）单位长度时的弹力。倔强系数跟弹簧的长度、弹簧的材料、弹簧丝的粗细等等都有关系。弹簧丝粗的硬弹簧比弹簧丝细的软弹簧倔强系数大。对于直杆和线的拉伸（或压缩）形变，也有上述正比关系。这个规律是英国科学家胡克发现的，叫做胡克定律。

胡克定律有它的适用范围。物体的形变过大，超出一定限度，上述正比关系将不再适用，这时即使撤去外力，物体也不能完全恢复原状，这个限度叫做弹性限度，胡克定律在弹性限度内适用，弹性限度内的形变叫做弹性形变。本书中提到的形变，除非特别指明，一般是指弹性形变。

练习二

（1）把一个重量为 2 N 的物体挂在弹簧上，物体静止时受到的弹簧的弹力有多大？为什么？

（2）把重量相同的两个物体分别挂在两根不同的弹簧上，一根弹簧伸长的长度小，另一根伸长的长度大。哪根弹簧的倔强系数大？

（3）一根弹簧的倔强系数是 100 N/m，伸长的长度为 2 cm 时，弹簧的弹力有多大？另一根弹簧的倔强系数是 2000 N/m，缩短的长度为 3 cm 时，弹簧的弹力有多大？

（4）一根弹簧，不挂物体时长 15cm，挂上 0.5 kg 的物体时长 18 cm。这根弹簧的倔强系数有多大？

发布时间：2015/6/17 上午7:13:18  阅读次数：2655