创新就要允许犯错误

马克思说：科学的入口处就像地狱之门。

佛说：我不入地狱，谁入地狱。

创新是大好事，我们这个古老的民族太需要创新了。对创新的好处已有不少论述，这里想谈谈创新过程的艰辛。创新是对未知境界的探索，你要去的地方是从未有人到过的，创新之路要靠自己走出来。缺乏坚韧不拔、百折不回的毅力，很难摘取创新之果。

1995年5月权威性的《数学年刊》刊载了英国数学家韦尔斯（A．Wiles，1953-）证明费马大定理的长篇论文。由于这一成就，韦尔斯几乎囊括了数学界所有的大奖，包括著名的沃尔夫奖、费马奖、科尔奖、肖克奖，等等。尤其是被誉为相当于数学诺贝尔奖之菲尔兹奖，本来只授予不超过40岁的数学家，这次专门为他颁发了一个特别奖。韦尔斯获此殊荣当之无愧，他攻下了350多年来数学史上最大的难题。

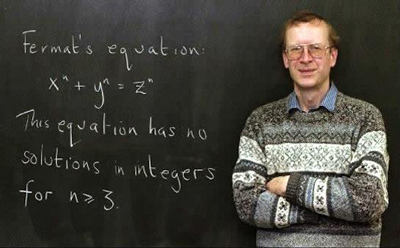
费马是法国数学家，自学成才，曾提出并证明过许多数学定理。他提出费马大定理，但并末给出证明，只是一个猜想。还有一个有趣的小插曲：1637年费马在一本拉丁文书《算术》中的第八个问题旁边空白处写下了这个猜想，接着他写道：“我对此已经有了一个确实非常奇妙的证明，只是此处空白太小，写不下。”后人曾为此专访费马故居，翻遍他的手稿，始终未发现有关的证明。这种轶事流传至今，为费马大定理平添了几分传奇色彩。

中学生都知道直角三角形的勾股（弦）定理：x²＋y²＝z²，其中x、y、z分别为勾、股、弦的长度。巧妙的是x、y、z可以是整数，例如《周髀算经》记载的“勾三股四弦五”，即x＝3，y＝4，z＝5，就是一组能满足该式的整数解。古希腊的毕达哥达斯学派对之曾进行过深入的探讨，找到了许多组整数解。他们还考察过：x³＋y³＝z³，出乎意料，始终无人能找出满足此式的x、y、z之非零整数解。费马考察了一般公式：xⁿ＋yⁿ＝zⁿ，其中n是大于2的整数。他费尽心机，始终找不到非零整数解，于是提出猜想：xⁿ＋yⁿ＝zⁿ，对于n大于2的整数，不存在x、y、z之非零整数解。”这就是著名的费马大定理，就这么简单，中学生也看得懂。

费马大定理虽然简单，证明却难于上青天。许多数学大师包括德国的莱布尼茨（Leibniz，1646-1716）和高斯（G．F．Gauβ，1777-1855），瑞士的欧拉（L．Euler，1707-1783），法国的勒让德（A．M．Legendre，1752-1833）和柯西（A．L．Cauchy，1789-1857）……都曾试图证明费马大定理，其他数学家以及业余爱好者尝试的更是不计其数，但是统统失败了。曾多次有人宣布证明了费马大定理，仅在1909年至1911年这三年内就提出了一千多篇证明，都因为有人指出证明中有漏洞而被否定了。还有人为此废寝忘食、神魂颠倒，甚至有自杀的。

韦尔斯10岁时在一本书中接触到费马大定理，马上被迷住了，立志要证明它——初生之犊不畏虎！他的数学老师并未认为他年幼无知而一笑置之，而是不断鼓励他、引导他，为他介绍必要的基础知识。韦尔斯从剑桥大学毕业后，1980年到美国普林斯顿大学做研究，这些年来他从未忘掉求证费马大定理。1986年他下决心攻这个难题，但能否成功，他没有把握。如果心无旁骛专攻费马大定理，不知何时才能发表论文。教授必须经常发表论文，否则就有碍声誉和发展前途。韦尔斯终于想出了两全之计：将自己在其他课题取得的成果写成若干篇论文，留着以后慢慢发表。韦尔斯开始潜心专攻费马大定理，他很快发现问题极为复杂——当然！否则早就有人解决了。为了求证费马大定理，不仅要用到最新的数学成果和技巧，而且还需要创造出新的方法，韦尔斯为了避免干扰，闭门谢客，此事除妻子外无人知晓。画壁七载，终于“大功告成”。韦尔斯写出了证明费马大定理的论文，1993年6月21日应邀在剑桥大学的国际数学讨论会上宣读。前一天在电脑网络中已有传言说韦尔斯的论文可能有关费马大定理，会场上座无虚席，走道上也站满了好奇的学生。韦尔斯的论文宣读持续了三天，黑板上写满一排排公式，擦掉后又写满了，两百多位听众急切地想知道结果到底如何。直到6月23日快结束时，韦尔斯才在黑板上写出了费马大定理，然后转过身来谦逊地说：“我想就到此为止。”费马大定理终于被证明了！大厅里响起一片掌声，纷纷向韦尔斯祝贺，消息马上传遍全世界。

可惜高兴得太早了，不久就在韦尔斯的证明中发现了漏洞。数学证明中出现漏洞可不是一件小事，证明定理全靠严密的逻辑推理，从前提到结论一步一步环环相扣，不能有一个环节脱扣，否则前功尽弃。对韦尔斯来说，如果这个漏洞补不起来，千里长堤溃于一穴，七载艰辛付诸东流。而且将不成熟的论文公开发表也是丢脸的事，韦尔斯这个错误犯大了！但他没有灰心，马上找了他的一个学生，两人一起着手补救，又是一年多功夫，皇天不负苦心人，漏洞终于补起来了。韦尔斯终算幸运，类似情况下漏洞补不起来的，大有人在。

想想看：费马大定理从提出到最终获得证明，350多年来多少人（包括韦尔斯在内）犯过多少错误，才取得最后成功。科学史上这种事屡见不鲜。牛顿在谈到自己成就时说：“我站在巨人的肩上。”他所说的巨人是为牛顿学说奠基的伽利略和开普勒等成功的先行者，但还应该看到，巨人脚下躺着无数筚路蓝缕、前仆后继的失败的先行者，是他们提供了宝贵的经验教训，使后人知所趋避。我国著名数学家陈省身说：“数学是‘胜者为王’，只有第一，没有第二。”其实一切科学均如此，重复别人就不算创新。但古往今来究竟有几个第一呢？没有那些第二、第三、……以及无数失败者组成的广大后备军，难道第一会从天而降？所以应该允许犯错误，不能完全以成败论英雄，要尊敬那些付出过艰辛劳动虽败犹荣的失败者。

有人说：“你举出的都是科学史上的大难题，我几次创薪一帆风顺，不曾犯错误。”我相信确实有这样的事。对此我只能说：“祝贺你创新成功！你一定很聪明勤奋，而且非常幸运。”一个人能当幸运儿是福气，但对国家社会而言，创新大业不能靠碰运气。所以我坚持：创新就要允许犯错误。道理很简单：创新是探索未知领域，无先例可循。提出的主意不可能保证绝对正确，因为要根据已有的理论或先例才能在事先证明其正确性，但这样一来就毫无新意了。再说：人非圣贤，孰能无过？

美国企业提倡创新，许多成果都出在小公司，因为他们敢于承担风险。大公司往往比较保守，员工们多一事不如少一事；经理们怕影响自己升迁，也尽量避免风险。但商场竞争是无情的，尤其是在高科技领域，不能创新就等于死亡。有鉴于此，一些有远见的大公司如IBM、杜邦等都建立了院士（Fellow）制度，并冠以公司之名，如IBM Fellow等，院士的特权有三：经费、时间、自由。每人都有相当大一笔院士基金，可以自行支配；院士三五年不出成果无人过问；关键是自由，院士喜欢干什么就干什么，想怎么做就怎么做，错了不要紧，重新再来过。事实证明：给科学家队自由，为他们创造必要的条件，让他们放手去干，允许犯错误，这样持之以恒，就能创新出大成果。IBM的几位科学家先后在扫描隧道显微镜和高温超导体方面获得了诺贝尔奖，最近又在集成电路中以铜代铝技术方面取得突破，提高了电脑的性能。此外，数学的一个分支“分形理论”能解释许多自然现象，并在不同领域内得到应用，其开创者也是一位IBM Fellow。经验表明，这种制度行之有效，对创新大有裨益。我国在有条件的地方，是否可以仿行？

发布时间：2015/2/21 上午10:53:38  阅读次数：3704