测出向心力

实验内容

把不锈钢丝穿过树脂管，在两端挂上砝码。一边旋转一端的砝码，一边确认另一端砝码在管子内的位置，从而求出向心力F。从砝码旋转周期的关系看看向心力F是否等于mrω²。

所需材料

树脂管（内径25.5mm、长50cm）、砝码（带钩子的圆筒形，外形24mm，20g）3～4个、秒表、不锈钢丝（粗0.8mm、长90cm）。

注意事项

注意要保证作为旋转中心的树脂管的轴一直垂直，并无大的摇摆。

实验方法

1．为了得知旋转的不锈钢丝的长度l，从树脂管的上端开始s处套上橡皮圈当作刻度。例如：s＝30cm，l＝60cm，则r＝\(\sqrt {{l^2} - {s^2}} \)≈52cm。

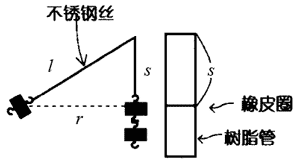
2．把不锈钢丝穿过树脂管的轴心，在两端挂上带钩子的砝码。砝码数量最开始为2个。随着向心力的增加相应增加数量。

3．在保持树脂管的轴垂直的同时，让砝码做匀速圆周运动。让砝码①旋转，让砝码②的上端与砝码①的旋转面与橡皮圈的位置在同一平面上。一边在旋转着的砝码①的内侧确认，一边适当调整匀速圆周运动的周期。让旋转面保持水平。

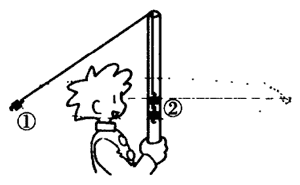
4．测量转100圈的时间，用1/100的倍数求出周期。

5．求出向心力F为Nmg•\(\frac{r}{l}\) ，Fʹ＝Nmg（N＝2、3）

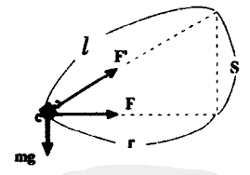
6．看看在第5步中求出的向心力F与mrω²与mr(\(\frac{{2\pi }}{T}\))²。

发布时间：2014/11/27 下午7:01:50  阅读次数：6295