3.5 转换矩阵与坐标转换矩阵的对比

在前面的几节中，我们已经区分了active变换（缩放、旋转和平移）和坐标转换变换。本节我们将会证明两者在数学上是等价的，一个active变换可以解释为一个坐标转换变换，反之亦然。

图3.15说明了公式3.7中的行向量（仿射矩阵变换实现的平移加旋转）与公式3.9中的行向量（坐标转换矩阵）的相似之处。

这是说得通的。在坐标转换变换的情况中，参考系的位置和朝向都是不同的。所以，将一个参考系变换到另一个参考系的数学方程需要旋转和平移坐标，最终我们会得到相同的数学形式。无论哪种情况，我们都会得到相同的数字；区别只是在于我们解释变换的方式。在某些情况下，使用多个坐标系统更符合思维习惯，我们可以让物体自身保持不变，只是从一个参考系转换到另一个参考系，由于参考系发生了改变，因此物体的坐标也会随之改变（这种情况对应图3.15b）。在另一些情况中，我们不想改变参考系，而只想在同一个参考系中对物体进行变换（这种情况对于图3.15a）。

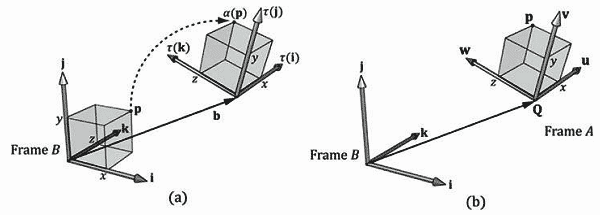
注意：上述讨论表明，我们可以将一个active变换组合（缩放，旋转，平移）解释为坐标系转换。这一点很重要，因为我们常常会将世界空间（第5章）的坐标变换矩阵定义为一个缩放、旋转、平移变换的组合。

发布时间：2014/10/7 下午8:37:48  阅读次数：5687