3.4 坐标转换变换
标量100℃是相对于摄氏温标表示的水的沸点温度。那么我们该如何以华氏温标来描述的水的沸点温度呢?换句话说就是在华氏温标中表示水的沸点温度的标量是多少?要实现这一转换(或参考系变换),我们需要知道摄氏与华氏之间的比例关系。它们的关系如下:TF=\(\frac{9}{5}\)TC+32°。因此,TF=\(\frac{9}{5}\)(100)°+32°=212℉;也就是,水的沸点温度为华氏212℉。
这个例子说明,只要我们知道参考系A和参考系B的关系,就可以将一个相对于参考系A标量k转换为相对于参考系B描述的等价标量kʹ。在下面的小节中,我们会看到一些类似的问题,但不是标量而是坐标,我们会将一个点或向量的坐标从一个参考系转换到另一个不同的参考系(参见图3.10)。我们将这种把坐标从一个参考系转换到另一个参考系的变换称为坐标转换变换(change of coordinate transformation)。
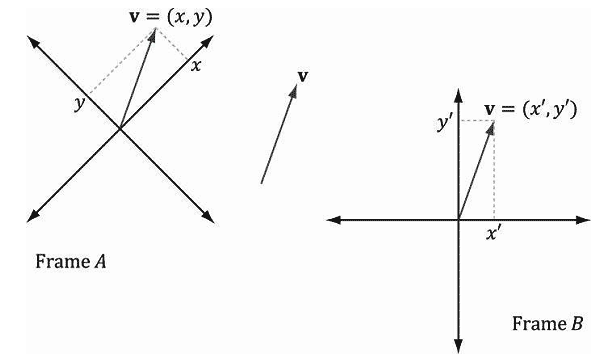
值得强调的是,在坐标转换变换中,我们并不认为几何体发生了什么改变;而是认为我们对参考系进行了转换,改变了几何体坐标的表达方式。相比之下,我们通常认为旋转、平移和缩放会对几何体产生实质性的移动或变形。
在3D计算机绘图中,由于我们会用到很多种不同坐标系,所以我们需要知道如何从一种坐标系转换到另一种坐标系。由于位置是点的属性,而不是向量的属性,所以点和向量在实现坐标转换变换时要区别对待,使用不同的处理方式。
3.4.1 向量
考虑图3.11中的两个参考系A、参考系B及向量p。假设p在参考系A中的坐标为pA=(x,y),我们想要求出p相对于参考系B的坐标pB= (xʹ,yʹ)。换句话说,在一个参考系中通过一个坐标指定一个向量,我们将个向量保持不变,只更换一个不同的参考系,那我们该如何求出这个向量的新坐标呢?
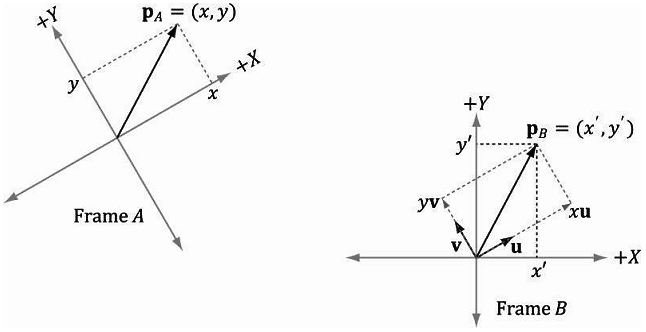
从图3.11可知
p=xu+yv
其中u和v是单位向量,它们所指向的方向分别与参考系A的x轴和y轴方向相同。通过上述方程,我们可以得到每个向量在参考系B中的坐标:
pB=xuB+yvB
这样,只要我们知道向量u、v相对于参考系B的坐标,即uB=(ux,uy)和vB=(vx,vy),那么对于给出的任意pA=(x,y),都可以计算出pB= (xʹ,yʹ)。
推导为3D向量,如果pA= (x,y,z),则
pB=xuB+yvB+zwB
其中u、v、w是单位向量,它们所指向的方向分别与参考系A的x轴、y轴、z轴方向相同。
3.4.2 点
当进行坐标转换变换时,点与向量之间存在一些微小差异;由于位置是点的一个重要属性,所以我们不能按照图3.11中的平移向量的方式来平移点。
图3.12说明了这一情况。我们看到,点p可以由一个方程来表示:
p=xu+yv+Q
其中u和v是单位向量,它们所指向的方向分别与参考系A的x轴和y轴方向相同,Q是参考系A的原点。通过上述方程,我们可以得到向量或点在参考系B中的坐标:
pB=xuB+yvB+QB
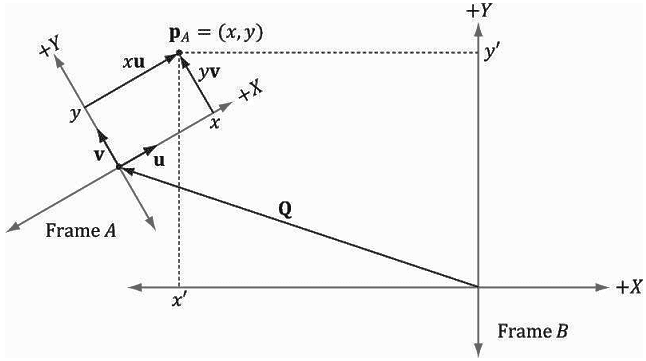
这样,只要我们知道向量u、v的坐标以及相对于参考系B的原点,即uB=(ux,uy)、vB=(vx,vy)、QB=(Qx,Qy),那么对于给出的任意坐标pA=(x,y),都可以求出pB=(xʹ,yʹ)。
推导为3D向量,如果pA=(x,y,z),则
pB=xuB+yvB+zwB+QB
其中u、v、w是单位向量,它们所指的方向分别与参考系A的x轴、y轴、z轴方向相同,Q是参考系A的原点。
3.4.3 矩阵表示
回顾之前讲过的内容,向量和点的坐标转换变换分别为:
(xʹ,yʹ,zʹ)=xuB+yvB+zwB用于向量
(xʹ,yʹ,zʹ)=xuB+yvB+zwB+QB用于点
如果我们使用齐次坐标,那么就可以通过一个方程同时处理向量和点:
\((x',y',z',w) = x{{\bf{u}}_B} + y{{\bf{v}}_B} + z{{\bf{w}}_B} + w{{\bf{Q}}_B}\)(公式3.8)
当w设为0时,该方程可用于处理向量的坐标转换变换;当w设为1时,该方程可用于处理点的坐标转换变换。方程3.8的优点在于只要我们给出正确的w坐标,就可以同时完成向量和点的处理;不再需要定义两个方程(一个用于向量,另一个用于点)。方程2.3说明,我们可以用矩阵的形式来表示方程3.8:
\(\begin{array}{l}\left[ {x',y',z',w} \right] = \left[ {x,y,z,w} \right]\left[ {\begin{array}{*{20}{c}}{ \leftarrow {{\bf{u}}_B} \to }\\{ \leftarrow {{\bf{v}}_B} \to }\\{ \leftarrow {{\bf{w}}_B} \to }\\{ \leftarrow {{\bf{Q}}_B} \to }\end{array}} \right]\\ = \left[ {x,y,z,w} \right]\left[ {\begin{array}{*{20}{c}}{{u_x}}&{{u_y}}&{{u_z}}&0\\{{v_x}}&{{v_y}}&{{v_z}}&0\\{{w_x}}&{{w_y}}&{{w_z}}&0\\{{Q_x}}&{{Q_y}}&{{Q_z}}&1\end{array}} \right]\end{array}\)(公式3.9)
其中QB=(Qx,Qy,Qz,1)、uB= (ux,uy,uz,0)、vB=(vx,vy,vz,0)、wB=(wx,wy,wz,0)均为齐次坐标,它们描述了参考系A相对于参考系B的原点位置和坐标轴方向。我们将方程3.9中的4×4矩阵称为坐标转换矩阵或参考系转换矩阵,它可以将参考系A的坐标转换(或映射)为参考系B的坐标。
3.4.4 结合律与坐标转换矩阵
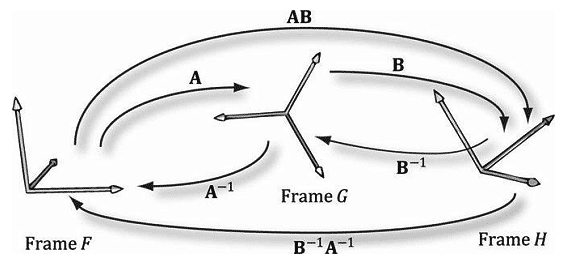
假设现在我们有3个参考系F、G、H。而且,设A为从F到G的参考系转换矩阵,设B为从G到H的参考系转换矩阵。假设pF为参考系F中的一个向量坐标,我们想要求解这个向量相对于参考系H的坐标,也就是求解pH。一种方法是将每个转换矩阵逐一相乘:
\[\begin{array}{l}({{\bf{p}}_F}{\bf{A}}){\bf{B}} = {{\bf{p}}_H}\\({{\bf{p}}_G}){\bf{B}} = {{\bf{p}}_H}\end{array}\]
不过,由于矩阵乘法支持结合律,所以我们可以将(pFA)B=pH改写为:
\[{{\bf{p}}_F}({\bf{AB}}) = {{\bf{p}}_H}\]
从这一意义上说,矩阵乘积C=AB可以被看成是从F直接向H的参考系转换矩阵;它将A和B产生的结果组合成了一个净矩阵。(这就像是把多个函数组合起来一样。)这种方法有助于提升性能。比如,我们将两个连续的坐标转换变换应用于一个由20,000个点构成的3D物体。使用逐一相乘的方式,我们需要执行20,000×2次向量-矩阵乘法。而改用组合矩阵方式, 我们只需要执行20,000次向量-矩阵乘法和一次矩阵-矩阵乘法。很明显,一次额外的矩阵-矩阵乘法所产生的资源消耗微乎其微,而它们却能省去大量的向量-矩阵乘法。
注意:我们再次强调,矩阵乘法不支持交换律,AB和BA表示不同的组合变换。矩阵相乘的顺序就是应用变换的顺序,这通常是一个不可交换的过程。
3.4.5 逆矩阵与坐标转换矩阵
假设pB为向量p在参考系B中的坐标,M为参考系A到参考系B的坐标转换矩阵;也就是pB=pAM。现在我们想求解pA。换句话说,就是使用坐标转换矩阵把从A到B的映射反转为从B到A的映射。如果M是一个可逆矩阵(即,M-1存在),那么就可以求出结果。我们可以按照如下步骤求解pA:
| pB=pAM | |
| pBM-1=pAMM-1 | 等式两边同时乘以M-1。 |
| pBM-1=pAI | 由逆矩阵的定义可知MM-1=I。 |
| pBM-1=pA | 由单位矩阵的定义可知pAI= pA。 |
这样,矩阵M-1即为从B到A的坐标转换矩阵。
图3.13说明了坐标转换矩阵与它的逆矩阵之间的关系。另外请读者注意,在本书中使用的所有坐标系转换映射都是可逆的,所以我们不必担心其逆矩阵是否存在。

图3.14说明了逆矩阵的特性(AB)-1 =B-1A-1可以被用于任何坐标转换矩阵。
发布时间:2014/10/3 下午8:47:28 阅读次数:6540
