3.3 组合变换

假设S是一个缩放矩阵，R是一个旋转矩阵，T是一个平移矩阵；另外，我们有一个由8个顶点v_i（i=0，1，…，7）构成的立方体，我们希望将这3个变换连续应用于立方体的每个顶点。一种最容易想到的方法是将这些矩阵逐一应用于每个顶点：

((v_iS)R)T = (v_iʹR)T= v_iʺT = v_i‴ 其中i=0，1，…，7

但是，由于矩阵乘法支持结合律，所以我们可以将上面的方程改为：

v_i(SRT) = v_i‴ 其中i=0，1，…，7

我们可以将SRT看成一个矩阵C，将所有的3个变换封装为一个净仿射变换矩阵。换句话说，矩阵-矩阵乘法可以让我们把多个变换连接在一起。

这种方法有助于提升性能。比如，我们将3个连续的几何变换应用于一个由20,000个点构成的3D物体。使用逐一相乘的方法，我们需要执行20,000×3次向量-矩阵乘法。而改用组合矩阵方式，我们只需要执行20,000次向量-矩阵乘法和两次矩阵-矩阵乘法。很明显，两次额外的矩阵-矩阵乘法所产生的资源消耗微乎其微，而它们却能省去大量的向量-矩阵乘法。

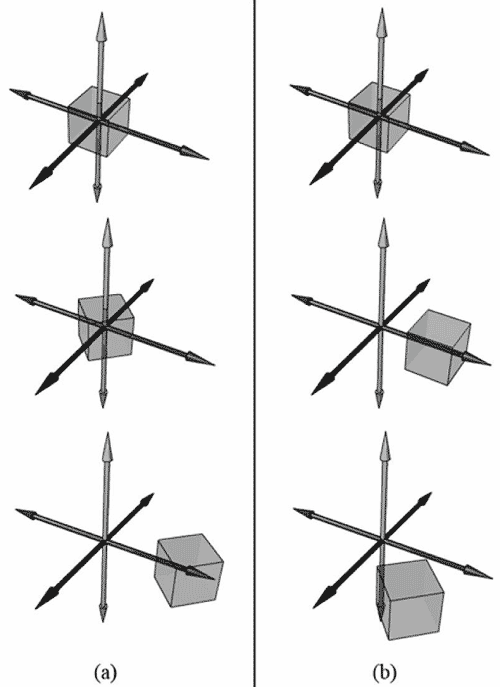
注意：我们再次强调，矩阵乘法不支持交换律。这完全符合于几何学中的定义。例如，在旋转之后进行一次平移，可以由矩阵乘积RT表示，但是它的结果与TR完全不同，也就是，在相同的平移之后进行一次相同的旋转，得到的变换结果完全不同。图3.9说明了这一点。

发布时间：2014/10/2 下午3:15:18  阅读次数：4288