3.2 仿射变换
3.2.1 齐次坐标
下一节我们就会知道仿射变换(http://zh.wikipedia.org/wiki/仿射变换)是一个组合了平移的线性变换。但是,因为向量只表示方向和长度,与位置无关,所以平移一个向量是无意义的,换句话说,平移后的向量是不变的。平移只能作用在点上(即,位置向量)。齐次坐标提供了一个便捷的表示方法用来统一处理点和向量。在齐次坐标中,我们使用4个元素,我们通过它的第4个坐标分量w来决定所描述的是一个点还是一个向量。确切地说,我们写为:
1.(x,y,z,0)用于向量
2.(x,y,z,1)用于点
我们将会看到,把w设为1是为了让点的平移操作得到正确执行,把w设为0是为了防止向量在变换过程中发生平移。(我们不希望平移向量的坐标,因为向量可以改变的只有方向和大小——平移对向量来说没有意义。)
注意:齐次坐标的记法与图1.17所示的概念一致。也就是,两点相减q−p= (qx,qy,qz,1) − (px,py,pz,1) = (qx – px,qy – py,qz – pz, 0)的结果是一个向量,而一个点与一个向量相加p+v=( px,py,pz,1) + (vx,vy,vz,0) = (px + vx,py + vy,pz + vz, 1)的结果是个点。
3.2.2 定义和矩阵表示
一个线性变换无法表示所有我们需要的变换;所以,我们需要添加一组叫做仿射变换的函数。仿射变换是一个线性变换加上一个平移向量b;也就是:
\[\alpha ({\bf{u}}) = \tau ({\bf{u}}) + b\]
或者用矩阵表示为:
\[\alpha ({\bf{u}}) = {\bf{uA}} + {\bf{b}} = [x,y,z]\left[ {\begin{array}{*{20}{c}}{{A_{11}}}&{{A_{12}}}&{{A_{13}}}\\{{A_{21}}}&{{A_{22}}}&{{A_{23}}}\\{{A_{31}}}&{{A_{32}}}&{{A_{33}}}\end{array}} \right] + [{b_x},{b_y},{b_z}] = [x',y',z']\]
式中的A是线性变换的矩阵表示。如果使用w=1的齐次坐标,则可表示为:
\(\left[ {x,y,z,1} \right]\left[ {\begin{array}{*{20}{c}}{{A_{11}}}&{{A_{12}}}&{{A_{13}}}&0\\{{A_{21}}}&{{A_{22}}}&{{A_{23}}}&0\\{{A_{31}}}&{{A_{32}}}&{{A_{33}}}&0\\{{b_x}}&{{b_y}}&{{b_z}}&1\end{array}} \right] = \left[ {x',y',z',1} \right]\)(公式3.6)
公式3.6中的4×4矩阵称为仿射矩阵的矩阵表示。
额外添加的b就是指平移(即,位置的改变)。因为向量没有位置的概念,所以我们并不想将b作用在向量上。但是,我们还是想将仿射矩阵的线性变换部分作用在向量上。如果我们把向量的第四个分量w设置为0,那么b对应的平移部分就不会作用到向量上。
注意:因为行向量与4×4仿射矩阵第4列的点乘是[x , y , z , w]•[0, 0, 0, 1] = w,所以这个矩阵不会改变输入向量的w坐标。
3.2.3 平移
单位变换(identity transformation)是一个线性变换,返回值就是输入的向量;即,I(u)=u。这说明线性变换的矩阵表示就是一个单位矩阵。
现在,我们将一个平移变换定义为一个仿射变换,这个仿射变换的线性变换部分是一个单位变换;即:
\[\tau ({\bf{u}}) = {\bf{uI}} + {\bf{b}} = {\bf{u}} + {\bf{b}}\]
如你所见,这可以简化将点u移动b的操作。图3.5说明了如何平移物体——要对点u进行平移,只需要将一个移位向量b和该点相加,即可得到新的点u+b。注意,要平移一个完整的物体,我们就要通过相同的向量b来平移物体上的每个点。
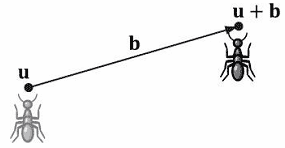
根据公式3.6,τ的矩阵表示如下:
\[{\bf{T}} = \left[ {\begin{array}{*{20}{c}}1&0&0&0\\0&1&0&0\\0&0&1&0\\{{b_x}}&{{b_y}}&{{b_z}}&1\end{array}} \right]\]
这个矩阵称之为平移矩阵。
平移矩阵的逆矩阵如下:
\[{{\bf{T}}^{ - 1}} = \left[ {\begin{array}{*{20}{c}}1&0&0&0\\0&1&0&0\\0&0&1&0\\{ - {b_x}}&{ - {b_y}}&{ - {b_z}}&1\end{array}} \right]\]
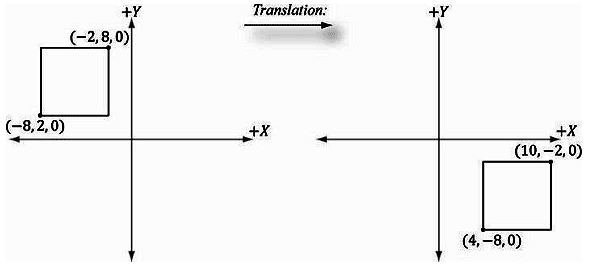
例3.4
假设我们通过一个最小点(−8, 2,0)和一个最大点(−2, 8,0) 来定义一个正方形。让正方形沿x轴平移12,沿y轴平移-10,z轴保持不变。则对应的平移矩阵如下:
\[{\bf{T}} = \left[ {\begin{array}{*{20}{c}}1&0&0&0\\0&1&0&0\\0&0&1&0\\{12}&{ - 10}&0&1\end{array}} \right]\]
现在,对正方形进行平移(变换),将正方形的两个点与该矩阵相乘:
\[\begin{array}{l}\left[ {\begin{array}{*{20}{c}}{ - 8}&2&0&1\end{array}} \right]\left[ {\begin{array}{*{20}{c}}1&0&0&0\\0&1&0&0\\0&0&1&0\\{12}&{ - 10}&0&1\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}4&{ - 8}&0&1\end{array}} \right]\\\left[ {\begin{array}{*{20}{c}}{ - 2}&8&0&1\end{array}} \right]\left[ {\begin{array}{*{20}{c}}1&0&0&0\\0&1&0&0\\0&0&1&0\\{12}&{ - 10}&0&1\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{10}&{ - 2}&0&1\end{array}} \right]\end{array}\]
结果如图3.6所示。
注意:令T为一个变换矩阵,通过计算vT= v′就可以对点/向量进行变换。如果先使用T对点/向量进行变换,然后再使用逆矩阵T-1进行变换,我们就会得到初始的向量:vTT-1 = vI = v。换句话说,逆变换可以撤销变换。例如,如果我们将一个点沿x轴移动5,然后沿x轴移动-5,会又回到出发点。类似地有,将一个点沿y轴旋转30°,然后反向旋转30°,该点又回到了原来的位置。总而言之,逆变换矩阵的变换效果与变换相反,两者的组合会导致不产生变换效果。
3.2.4 缩放和旋转的仿射矩阵
若b=0,仿射变换就退化为一个线性变换。我们可以将任何一个线性变换表示成b=0的仿射变换。换句话说,我们可以用一个4×4仿射矩阵表示任意一个线性变换。例如,缩放和旋转矩阵可以用4×4矩阵写成如下形式:
\[{\bf{S}} = \left[ {\begin{array}{*{20}{c}}{{s_x}}&0&0&0\\0&{{s_y}}&0&0\\0&0&{{s_z}}&0\\0&0&0&1\end{array}} \right]\]
\[{{\bf{R}}_n} = \left[ {\begin{array}{*{20}{c}}{c + (1 - c){x^2}}&{(1 - c)xy + sz}&{(1 - c)xz - sy}&0\\{(1 - c)xy - sz}&{c + (1 - c){y^2}}&{(1 - c)yz + sx}&0\\{(1 - c)xz + sy}&{(1 - c)yz - sx}&{c + (1 - c){z^2}}&0\\0&0&0&1\end{array}} \right]\]
通过这种方式,我们使用4×4矩阵表示所有变换,使用1×4齐次行向量矩阵表示点和向量,形式得到了统一。
3.2.5 仿射变换矩阵的几何解释
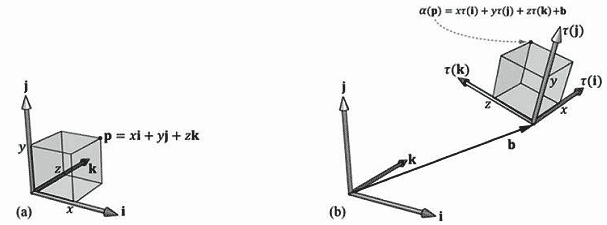
在本节中,我们会对一个仿射变换矩阵中的数字表示的几何意义有个直观的认识。首先,考虑一个刚体变换,它是一个形状保持不变的变换。现实世界中的例子是将一本书从桌上拿起放到书架上,在这个过程中,你将书从书桌平移到了书架,还改变了书的朝向(旋转)。令τ为旋转变换,b为位移矢量,则这个刚体变换可以用以下仿射变换表示:
\[\alpha (x,y,z) = \tau (x,y,z) + {\bf{b}} = x\tau ({\bf{i}}) + y\tau ({\bf{j}}) + z\tau ({\bf{k}}) + {\bf{b}}\]
在矩阵表示中,使用其次坐标(w=1表示位置,w=0表示向量,这样平移就不会作用在向量上),上式可以写成:
\(\left[ {x,y,z,w} \right]\left[ {\begin{array}{*{20}{c}}{ \leftarrow \tau ({\bf{i}}) \to }\\{ \leftarrow \tau ({\bf{j}}) \to }\\{ \leftarrow \tau ({\bf{k}}) \to }\\{ \leftarrow {\bf{b}} \to }\end{array}} \right] = \left[ {x',y',z',w} \right]\)(公式3.7)
现在看一下公式3.7的几何意义,我们只需画出矩阵中的行向量(参见图3.7)。因为τ是一个旋转变换,所以它保存了长度和角度信息;而且τ只是将标准基向量i,j和k旋转到一个新的朝向τ(i),τ(j)和τ(k)。向量b只是一个位置向量,它表示的是离开原点的位移。图3.7展示了如何通过计算\(\alpha (x,y,z) = x\tau ({\bf{i}}) + y\tau ({\bf{j}}) + z\tau ({\bf{k}}) + {\bf{b}}\)获得变换后的点。
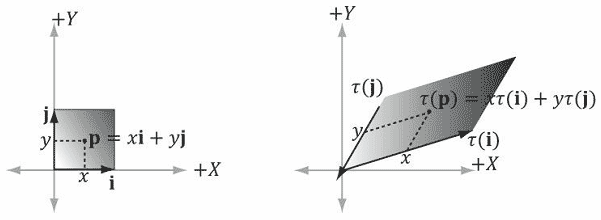
缩放和扭曲变换的原理相同。考虑线性变换τ,如图3.8所示,这个变换将正方形扭曲成一个平行四边形。扭曲后的点就是扭曲后的基向量的线性组合。
发布时间:2014/10/1 下午2:29:51 阅读次数:6342
