3.1 线性变换

我们以几何方式描述3D场景中的物体；也就是用一组三角形近似地模拟物体的外表面。如果我们创建的物体都静止不动，那么场景就会显得索然无趣。所以，我们必须学习对几何体进行变换的方法；常见的几何变换包括平移、旋转和缩放。本章会给出许多矩阵公式，读者可以使用些公式对3D空间中的点和向量进行变换。

学习目标

1．了解如何使用矩阵表示线性变换和仿射变换。

2．学习用于缩放、旋转和平移几何体的坐标变换。

3．了解如何通过矩阵-矩阵乘法将多个变换矩阵组合为一个净变换矩阵。

4．了解如何将坐标从一个坐标系转换到另一个坐标系，以及如何通过一个矩阵来描述坐标变换。

5．熟悉用于创建变换矩阵的函数，这些函数是XNA数学库的一个子集。

3.1.1 定义

考虑一个数学函数τ(v)= τ(x,y,z) = (xʹ,yʹ,zʹ)。这个函数的输入和输出都是一个3D向量。当且仅当τ满足以下性质时我们才认为它是一个线性变换：

\(\begin{array}{l}1.\tau ({\bf{u}} + {\bf{v}}) = \tau ({\bf{u}}) + \tau ({\bf{v}})\\2.\tau (k{\bf{u}}) = k\tau ({\bf{u}})\end{array}\)（公式3.1）

其中u=(u_x,u_y,u_z) 和v = (v_x,v_y,v_z)为任意3D向量，k是一个标量。

注意：线性变换的输入和输出不一定是3D向量，但在3D图形学的书中我们无需使用其他更普遍的形式。

例3.1

定义一个函数τ(x,y,z) = (x²,y²,z²)；例如，τ(1,2,3) =(1,4,9)。这个函数不是线性的，这是因为若k=2、u=(1,2,3)，我们可以得到：

τ(ku) = τ(2, 4, 6) = (4, 16, 36)

但

kτ(u) = 2 (1, 4, 9) = (2, 8, 18)

所以不满足公式3.1。如果τ是线性的，它应该满足下面的式子：

\(\begin{array}{l}\tau (a{\bf{u}} + b{\bf{c}} + c{\bf{w}}) = \tau (a{\bf{u}} + (b{\bf{v}} + c{\bf{w}}))\\ = a\tau ({\bf{u}}) + \tau (b{\bf{v}} + c{\bf{w}})\\ = a\tau ({\bf{u}}) + b\tau ({\bf{v}}) + c\tau ({\bf{w}})\end{array}\)（公式3.2）

我们会在下一节中使用这个结果。

3.1.2 矩阵描述

令u=(x,y,z)。我们总可以写成下面的形式：

u= (x , y , z) = x i + y j + z k = x (1, 0, 0) + y (0, 1, 0) + z (0, 0, 1)

向量i = (1, 0, 0)，j = (0, 1, 0)和k = (0, 0, 1)都是沿着坐标轴的单位向量，我们把它们称为ℝ³的标准基向量（standard basis vectors）（ℝ³表示所有3D坐标向量(x , y , z)的集合）。令τ为线性变换，则根据线性函数的特点（即公式3.2），我们可以得到：

\(\tau ({\bf{u}}) = \tau (x{\bf{i}} + y{\bf{j}} + z{\bf{k}}) = x\tau ({\bf{i}}) + y\tau ({\bf{j}}) + z\tau ({\bf{k}})\)（公式3.3）

公式3.3其实就是一个线性组合，我们在上一章就已经讨论过了，这个线性组合可以根据公式2.2写成矢量与矩阵的乘法，因此我们可以将公式3.3重写成如下形式：

\(\begin{array}{l}\tau ({\bf{u}}) = x\tau ({\bf{i}}) + y\tau ({\bf{j}}) + z\tau ({\bf{k}})\\ = {\bf{uA}}{\rm{ = }}\left[ {x,y,z} \right]\left[ {\begin{array}{*{20}{c}} \leftarrow &{\tau ({\bf{i}})}& \to \\ \leftarrow &{\tau ({\bf{j}})}& \to \\ \leftarrow &{\tau ({\bf{k}})}& \to \end{array}} \right] = \left[ {x,y,z} \right]\left[ {\begin{array}{*{20}{c}}{{A_{11}}}&{{A_{12}}}&{{A_{13}}}\\{{A_{21}}}&{{A_{21}}}&{{A_{23}}}\\{{A_{31}}}&{{A_{32}}}&{{A_{33}}}\end{array}} \right]\end{array}\)（公式3.4）

其中τ (i) = (A₁₁, A₁₂ , A₁₃)，τ (j) = (A₂₁ , A₂₂, A₂₃)，τ (k) = (A₃₁, A₃₂, A₃₃)。

我们把矩阵A称为线性变换τ的矩阵描述。

3.1.3 缩放

缩放是指改变一个物体的大小，如图3.1所示。

我们将缩放变换定义为：

\[S(x,y,z) = ({s_x}x,{s_y}y,{s_z}z)\]

上述变换将向量沿x轴方向缩放s_x单位，y轴方向缩放s_y个单位，z轴方向缩放s_z个单位（相对于目前的坐标系原点）。下面我们证明S是一个线性变换：

\[\begin{array}{l}S({\bf{u}} + {\bf{v}}) = ({s_x}({u_x} + {v_x}),{s_y}({u_y} + {v_y}),{s_z}({u_z} + {v_z}))\\ = ({s_x}{u_x} + {s_x}{v_x},{s_y}{u_y} + {s_y}{v_y},{s_z}{u_z} + {s_z}{v_z})\\ = ({s_x}{u_x},{s_y}{u_y},{s_z}{u_z}) + ({s_x}{v_x},{s_y}{v_y},{s_z}{v_z})\\ = S({\bf{u}}) + S({\bf{v}})\end{array}\]

\[\begin{array}{l}S(k{\bf{u}}) = ({s_x}k{u_x},{s_y}k{u_y},{s_z}k{u_z})\\ = k({s_x}{u_x},{s_y}{u_y},{s_z}{u_z})\\ = kS({\bf{u}})\end{array}\]

满足公式3.1的两个性质，所以S是线性的，应该存在一个矩阵描述。要找到这个矩阵描述，我们只需将S代入公式3.3中的每个标准基向量中即可，然后将得出的结果向量替换矩阵的行：

\[\begin{array}{l}S({\bf{i}}) = ({s_x} \cdot 1,{s_y} \cdot 0,{s_z} \cdot 0) = ({s_x},0,0)\\S({\bf{j}}) = ({s_x} \cdot 0,{s_y} \cdot 1,{s_z} \cdot 0) = (0,{s_y},0)\\S({\bf{k}}) = ({s_x} \cdot 0,{s_y} \cdot 0,{s_z} \cdot 1) = (0,0,{s_z})\end{array}\]

S的矩阵表示为：

\[{\bf{S}} = \left[ {\begin{array}{*{20}{c}}{{s_x}}&0&0\\0&{{s_y}}&0\\0&0&{{s_z}}\end{array}} \right]\]

我们把这个矩阵叫做缩放矩阵。缩放矩阵的逆矩阵为：

\[{\bf{S}} = \left[ {\begin{array}{*{20}{c}}{1/{s_x}}&0&0\\0&{1/{s_y}}&0\\0&0&{1/{s_z}}\end{array}} \right]\]

例3.2

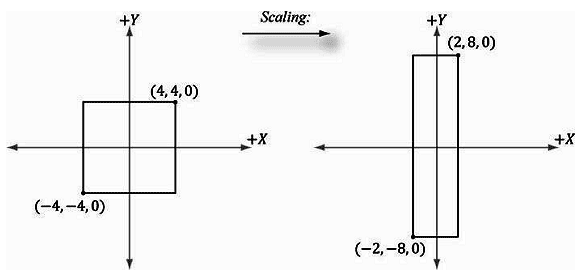
假设我们通过一个最小点(−4, −4,0)和一个最大点(4, 4,0)来定义一个正方形，我们希望将正方形沿x轴缩小0.5倍，沿y轴放大2.0倍，z轴保持不变。则对应的缩放矩阵为：

\[{\bf{S}} = \left[ {\begin{array}{*{20}{c}}{0.5}&0&0\\0&2&0\\0&0&1\end{array}} \right]\]

现在，对正方形进行缩放（变换），将正方形的两个点与该矩阵相乘：

\[\begin{array}{l}\left[ {\begin{array}{*{20}{c}}{ - 4}&{ - 4}&0\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{0.5}&0&0\\0&2&0\\0&0&1\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{ - 2}&{ - 8}&0\end{array}} \right]\\\left[ {\begin{array}{*{20}{c}}4&4&0\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{0.5}&0&0\\0&2&0\\0&0&1\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}2&8&0\end{array}} \right]\end{array}\]

结果如图3.2所示。

3.1.4 旋转

本节我们将介绍如何将向量v绕一根轴n旋转θ角度；如图3.3所示。注意，在左手坐标系中，当沿着旋转轴的正轴方向俯视时，顺时针方向为正角；而且，我们假设||n||=1。

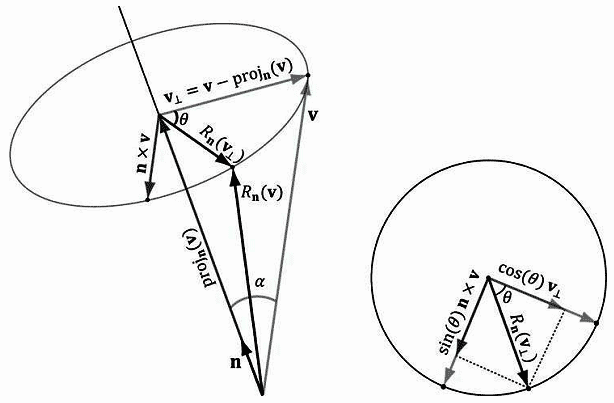
首先，将v分解为两个分量，其中一个分量平行于n，另一个垂直于n。平行分量即proj_n(v)（回忆一下例1.5）；垂直分量可以通过v_⊥= perp_n(v) = v – proj_n (v)得到（还是回忆一下例1.5，因为n是单位向量，所以proj_n(v) = (n•v)n。）。平行于n的proj_n(v)分量在旋转过程中是不变的，所以我们只需计算垂直分量的旋转。从图3.3中我们可以看出，旋转后的向量R_n(v) = proj_n(v) + R_n(v_⊥)。

要找到R_n(v_⊥)，我们需要建立一个位于旋转平面的2D坐标系。将v_⊥作为一个基准向量，第二个基准向量需要同时垂直于v_⊥和n，我们取为n × v（左手拇指定则）。根据图3.3中的几何关系和第一章的练习14，我们可以得出：

\[\left\| {{\bf{n}} \times {\bf{v}}} \right\| = \left\| {\bf{n}} \right\|\left\| {\bf{v}} \right\|\sin \alpha = \left\| {\bf{v}} \right\|\sin \alpha = \left\| {{{\bf{v}}_ \bot }} \right\|\]

其中α为n和v之间的夹角。这样这两个基准向量都有相同的长度并且都在旋转平面上。创建了两个基准向量后，我们就可以根据三角学的知识得出：

\[{R_n}({{\bf{v}}_ \bot }) = \cos \theta {{\bf{v}}_ \bot } + \sin \theta ({\bf{n}} \times {\bf{v}})\]

并由此得到下面的旋转方程：

\(\begin{array}{l}{R_n}({\bf{v}}) = pro{j_n}({\bf{v}}) + {R_n}({{\bf{v}}_ \bot })\\ = ({\bf{n}} \cdot {\bf{v}}){\bf{n}} + \cos \theta {{\bf{v}}_ \bot } + \sin \theta ({\bf{n}} \times {\bf{v}})\\ = ({\bf{n}} \cdot {\bf{v}}){\bf{n}} + \cos \theta ({\bf{v}} - ({\bf{n}} \cdot {\bf{v}}){\bf{n}}) + \sin \theta ({\bf{n}} \times {\bf{v}})\\ = \cos \theta {\bf{v}} + (1 - \cos \theta )({\bf{n}} \cdot {\bf{v}}){\bf{n}} + \sin \theta ({\bf{n}} \times {\bf{v}})\end{array}\)（公式3.5）

我们把证明公式3.5为一个线性变换放在了后面的练习中，这里不予讨论。要找到对应的矩阵描述，我们只需将R_n代入公式3.3中的每个标准基向量中即可，然后将得出的结果向量替换矩阵的行（即在公式3.4中）。最终结果为：

\[{{\bf{R}}_n} = \left[ {\begin{array}{*{20}{c}}{c + (1 - c){x^2}}&{(1 - c)xy + sz}&{(1 - c)xz - sy}\\{(1 - c)xy - sz}&{c + (1 - c){y^2}}&{(1 - c)yz + sx}\\{(1 - c)xz + sy}&{(1 - c)yz - sx}&{c + (1 - c){z^2}}\end{array}} \right]\]

其中c=cosθ，s=sinθ。

旋转矩阵有一个有趣的特性。读者可以验证一下：旋转矩阵的每个行向量都是单位向量，而且相互垂直。也就是说，它的每个行向量都是标准正交的（即，相互垂直且为单位长度）。我们将这种矩阵称为正交矩阵（orthogonal matrix）。正交矩阵有一个非常有用的特性，它的逆矩阵与它的转置矩阵相等。也就是，R_n的逆矩阵为：

\[{\bf{R}}_n^{ - 1} = {\bf{R}}_n^T = \left[ {\begin{array}{*{20}{c}}{c + (1 - c){x^2}}&{(1 - c)xy - sz}&{(1 - c)xz + sy}\\{(1 - c)xy + sz}&{c + (1 - c){y^2}}&{(1 - c)yz - sx}\\{(1 - c)xz - sy}&{(1 - c)yz + sx}&{c + (1 - c){z^2}}\end{array}} \right]\]

通常，正交矩阵是最容易使用的矩阵，因为它们计算逆矩阵的过程非常简单，也非常高效。当我们以x、y、z轴（即，n=(1, 0,0)、n= (0, 1,0)、n= (0, 0,1)）为旋转轴时，对应的旋转矩阵如下：

\[{{\bf{R}}_x} = \left[ {\begin{array}{*{20}{c}}1&0&0\\0&{\cos \theta }&{\sin \theta }\\0&{ - \sin \theta }&{\cos \theta }\end{array}} \right],{{\bf{R}}_y} = \left[ {\begin{array}{*{20}{c}}{\cos \theta }&0&{ - \sin \theta }\\0&1&0\\{\sin \theta }&0&{\cos \theta }\end{array}} \right],{{\bf{R}}_z} = \left[ {\begin{array}{*{20}{c}}{\cos \theta }&{\sin \theta }&0\\{ - \sin \theta }&{\cos \theta }&0\\0&0&1\end{array}} \right]\]

例3.3

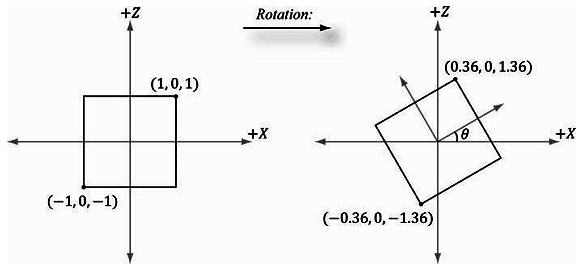
假设我们通过一个最小点(−1,0,−1)和一个最大点(1,0,1)来定义一个正方形。让正方形绕着y轴的顺时针方向旋转-30º（即，逆时针方向旋转30º）。在这种情况中，n=(0,1,0)，R_n大为简化；对应的y轴旋转矩阵为：

\[{{\bf{R}}_y} = \left[ {\begin{array}{*{20}{c}}{\cos \theta }&0&{ - \sin \theta }\\0&1&0\\{\sin \theta }&0&{\cos \theta }\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{\cos ( - 30^\circ )}&0&{ - \sin ( - 30^\circ )}\\0&1&0\\{\sin ( - 30^\circ )}&0&{\cos ( - 30^\circ )}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{\frac{{\sqrt 3 }}{2}}&0&{\frac{1}{2}}\\0&1&0\\{ - \frac{1}{2}}&0&{\frac{{\sqrt 3 }}{2}}\end{array}} \right] \approx \left[ {0.36,0,1.36} \right]\]

现在，对正方形进行旋转（变换），将正方形的两个点与该矩阵相乘：

\[\begin{array}{l}\left[ { - 1,0, - 1} \right]\left[ {\begin{array}{*{20}{c}}{\frac{{\sqrt 3 }}{2}}&0&{\frac{1}{2}}\\0&1&0\\{ - \frac{1}{2}}&0&{\frac{{\sqrt 3 }}{2}}\end{array}} \right] \approx \left[ { - 0.36,0, - 1.36} \right]\\\left[ {1,0,1} \right]\left[ {\begin{array}{*{20}{c}}{\frac{{\sqrt 3 }}{2}}&0&{\frac{1}{2}}\\0&1&0\\{ - \frac{1}{2}}&0&{\frac{{\sqrt 3 }}{2}}\end{array}} \right] \approx \left[ {0.36,0,1.36} \right]\end{array}\]

结果如图3.4所示。

发布时间：2014/9/28 下午9:24:53  阅读次数：5088