1.5 点

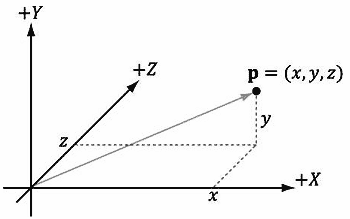
到目前为止，我们讨论的是与位置无关的向量。而我们在 3D 程序中需要描述坐标位置；比如，3D几何体的位置和 3D 虚拟摄像机的位置。相对于一个坐标系，我们可以使用在标准位置上的向量（参见图1.16）来表示空间中的3D位置； 我们将它称为位置向量（position vector）。在这里，向量末端的位置是唯一需要关注的特性，而方向和大小都无关紧要。我们会交替使用术语“位置向量”和“点”，因为位置向量表示的就是一个点。

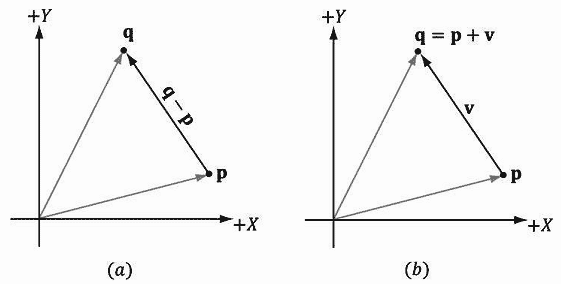
使用向量来表示点的一个好处是可以在代码中使用向量运算，虽然向量运算对点来说没有实际意义；比如，在几何学中，两点相加有什么意义？不过有一些运算确实可以被扩展为点运算。比如，两点之差q−p可以表示从p到q的向量。点p与向量v相加得到点q，可以认为q是v对p进行的平移。由于使用向量可以很方便地表示相对于坐标系的点，所以我们不必为单独设计一套针对于点的运算，只需要借助于前面讨论过的向量代数框架就可以处理它们（参见图1.17）。

注意：其实在几何学中有一种非常重要的方法叫做仿射组合（affine combination），它用于对点进行特殊的求和运算，就像是对点求加权平均值一样。

发布时间：2014/9/11 下午6:56:36  阅读次数：4202