1.3 点积

点积（dot product）是向量乘法的一种形式，它的计算结果是一个标量值；由于这一原因，有时也将点积称为标量积（scalar product）。设u=（u_x,u_y,u_z），v=（v_x,v_y,v_z），则点积定义如下：

\({\bf{u}} \cdot {\bf{v}} = {u_x}{v_x} + {u_y}{v_y} + {u_z}{v_z}\)    （1.3）

简言之，点积等于两个向量对应分量的乘积之和。点积的定义不存在任何明显的几何含义。但是，使用余弦定理可以发现存在如下关系：

\({\bf{u}} \cdot {\bf{v}} = \left\| {\bf{u}} \right\|\left\| {\bf{v}} \right\|\cos \theta \)    （1.4）

其中，θ表示向量u和v之间的夹角，且0≤θ≤π（参见图1.9）。公式1.4说明这两个向量的点积等于向量夹角的余弦值和向量模之间的乘积。在特殊情况下，如果u和v都是单位向量，那么u∙v就等于它们之间夹角的余弦值（即，u∙v=cosθ）。

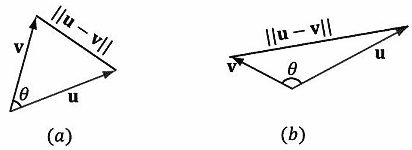
公式1.4提供了一些有用的点积的几何性质：

1．如果u∙v=0，则u⊥v（即，向量相互垂直）。

2．如果u∙v＞0，则两个向量之间的夹角θ小于90º（即，向量形成一个锐角）。

3．如果u∙v＜0，则两个向量之间的夹角θ大于90º（即，向量形成一个钝角）。

注意：“相互垂直”也可称为“互成直角”。

【例1.4】

设u=（1, 2,3）、v=（−4, 0, −1）。求u和v之间的夹角。首先，我们要做如下计算：

\(\begin{array}{l}{\bf{u}} \cdot {\bf{v}} = (1,2,3) \cdot ( - 4,0, - 1) = - 4 - 3 = - 7\\\left\| {\bf{u}} \right\| = \sqrt {{1^2} + {2^2} + {3^3}} = \sqrt {14} \\\left\| {\bf{v}} \right\| = \sqrt {{{( - 4)}^2} + {0^2} + {{( - 1)}^2}} = \sqrt {17} \end{array}\)

现在，由公式1.4解得θ为：

\(\begin{array}{l}\cos \theta = \frac{{{\bf{u}} \cdot {\bf{v}}}}{{\left\| {\bf{u}} \right\|\left\| {\bf{v}} \right\|}} = \frac{{ - 7}}{{\sqrt {14} \sqrt {17} }}\\\theta = {\cos ^{ - 1}}\frac{{ - 7}}{{\sqrt {14} \sqrt {17} }} \approx 117^\circ \end{array}\)

【例 1.5】

考虑图1.10。给出v和单位向量n，推导出一个使用点积求解向量p的公式。

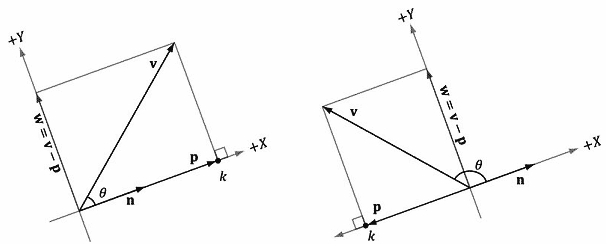
首先，从该图中可以看到标量k可以使p=kn；而且，由于我们已知‖n‖=1，所以有‖p‖=‖kn‖=| k|‖n‖=|k|。（注意，当且仅当p与n的方向相反时，k为负数。）我们使用三角函数，可以得出k=‖v‖cosθ；由此，p=kn=（‖v‖cosθ）n。不过，因为n是一个单位向量，所以我们可以用另一种方式进行表达：

\[{\bf{p}} = (\left\| {\bf{v}} \right\|\cos \theta ){\bf{n}} = (\left\| {\bf{v}} \right\| \cdot 1\cos \theta ){\bf{n}} = (\left\| {\bf{v}} \right\| \cdot \left\| {\bf{n}} \right\|\cos \theta ){\bf{n}} = ({\bf{v}} \cdot {\bf{n}}){\bf{n}}\]

请注意，这里的k=v∙n，它说明了当n为单位向量时v∙n的几何含义。我们将p称为v在n上的正交投影（orthogonal projection），并记为

\[{\bf{p}} = pro{j_{\bf{n}}}({\bf{v}})\]

如果我们把v理解为一个作用力，那么p可以被认为是v在方向n上的分力。同理，向量w=perp_n(v)=v−p是与n垂直方向上的分力。可以看到v=p+w，这说明我们已经将向量v分解成了两个相互垂直的向量p和w。如果n不是一个单位向量，那我们可以对它进行规范化，使其保持单位长度。通过用单位向量\(\frac{{\bf{n}}}{{\left\| {\bf{n}} \right\|}}\)来代替n，可以得到一个更通用的投影公式：

\[{\bf{p}} = pro{j_{\bf{n}}}({\bf{v}}) = ({\bf{v}} \cdot \frac{{\bf{n}}}{{\left\| {\bf{n}} \right\|}})\frac{{\bf{n}}}{{\left\| {\bf{n}} \right\|}} = \frac{{({\bf{v}} \cdot {\bf{n}})}}{{{{\left\| {\bf{n}} \right\|}^2}}}{\bf{n}}\]

1.3.1 正交化

若一个向量集合{v₀，……，v_n-1 }中的向量相互正交（即集合中的每一个向量与其他向量正交）并具有单位长度，我们将这个集合称之为规范化正交集。有时一组向量几乎是正交的，但又不完全是，一个常见的任务就是使其正交。在三维计算机图形中，开始时通常是一个规范化正交的向量集合，但由于计算精度问题，这个集合就会逐渐成为非规范化的了。我们主要关心的是2D和3D的情况下任何处理这个问题（即，含有两个和三个向量的情况）。

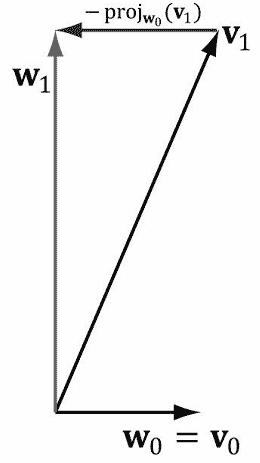
首先讨论简单的2D情况。假设有一组向量为{v₀,v₁}，我们要将它们正交到一个规范正交集{w₀,w₁}中，如图1.11所示。首先令w₀=v₀，然后修改v₁使它与w₀垂直；这需要减去v₁向量在w₀上的投影：

w₁= v₁- proj_w0(v₁)

现在就有了一组互相垂直的向量{w₀,w₁}；最后需要规范化w₀和w₁才能构建规范化的正交集。

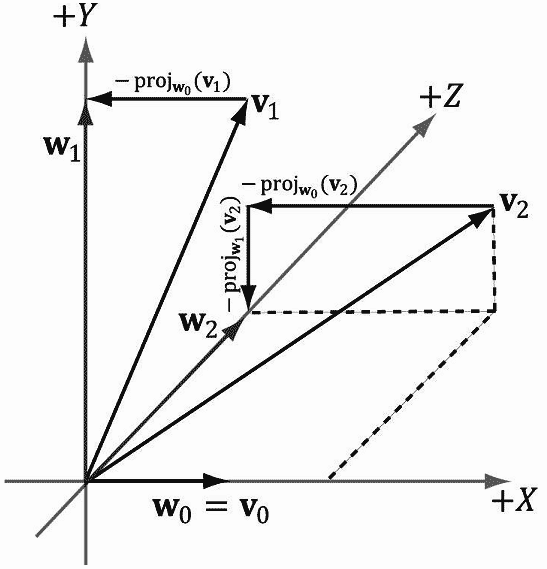
3D情况的原理与2D相同，但需要更多的步骤。假设有一组向量{v₀,v₁,v₂}需要正交规范化到{w₀,w₁,w₂}，如图1.12所示。首先令w₀=v₀，然后修改v₁使之垂直于w₀；这需要从v₁中减去v₁在w₀方向上的投影：

w₁= v₁- proj_w0(v₁)

下一步需要令v₂同时垂直于w₀和w₁，这需要从v₂中减去v₂在w₀上的投影再减去v₂在w₁上的投影：

w₂= v₂- proj_w0(v₂) - proj_w1(v₂)

现在就有了一组互相垂直的向量{w₀,w₁,w₂}；最后需要规范化w₀、w₁和w₂才能构建规范化的正交集。

要规范正交化任意数量的向量集{v₀,…,v_n-1}，我们需要按照通常叫做>Gram-Schmidt正交化(http://zh.wikipedia.org/wiki/格拉姆-施密特正交化)的处理过程进行：

基本步骤：令w₀=v₀

for 1 ≤ i ≤ n-1，令\({{\bf{w}}_i} = {{\bf{v}}_i} - \sum\limits_{j = 0}^{i - 1} {pro{j_{{\bf{wj}}}}({{\bf{v}}_{\bf{i}}})} \)

规范化步骤：令\({{\bf{w}}_i} = \frac{{{{\bf{w}}_i}}}{{\left\| {{{\bf{w}}_i}} \right\|}}\)

原理与上面是类似的，当选取一个向量vⁱ将它添加到规范化的正交集时，我们需要减去这个向量在正交集中其他向量（w₀,w₁,…,w_i-1）上的投影，这样可以确保这个新添的向量与正交集中的其他向量垂直。

发布时间：2014/9/8 下午8:15:03  阅读次数：5274