1.2 长度和单位向量

在几何学中，向量的大小等于有向线段的长度。我们用双竖线来表示向量的大小（例如，‖u‖表示u的大小）。现在，给出一个向量u=(x,y,z)，我们希望以代数方式计算它的大小。通过运用两次毕达哥拉斯定理可以计算出3D向量的大小（译者注：毕达哥拉斯定理和勾股定理的概念相同，换言之，毕达哥拉斯定理就是勾股定理）；参见图1.8。

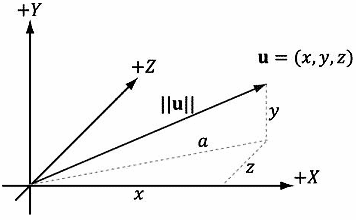
首先，我们来看xz平面上的三角形边x、z及斜边a。由毕达哥拉斯定理可知\(a = \sqrt {{x^2} + {z^2}} \) 。现在来看三角形边a、y及斜边‖u‖。通过再次使用毕达哥拉斯定理，可以得到如下求模公式：

\(\left\| {\bf{u}} \right\| = \sqrt {{y^2} + {a^2}} = \sqrt {{y^2} + {{(\sqrt {{x^2} + {z^2}} )}^2}} = \sqrt {{x^2} + {y^2} + {z^2}} \)    （1.1）

在某些应用中，我们不关心向量的长度， 只希望用向量来表示一个单纯的方向。对于这种只表示方向、不表示大小的向量，我们希望将其长度精确地设定为1。当我们想要让一个向量具有单位长度时，我们说要对该向量进行规范化。我们将向量的每个分量除以该向量的模，得到规范化向量：

\({\bf{\hat u}} = \frac{{\bf{u}}}{{\left\| {\bf{u}} \right\|}} = \left( {\frac{x}{{\left\| {\bf{u}} \right\|}},\frac{y}{{\left\| {\bf{u}} \right\|}},\frac{z}{{\left\| {\bf{u}} \right\|}}} \right)\)    (1.2)

要验证这个公式的正确性，只需计算\({\bf{\hat u}}\)的长度即可：

\[\left\| {{\bf{\hat u}}} \right\| = \sqrt {{{\left( {\frac{x}{{\left\| {\bf{u}} \right\|}}} \right)}^2} + {{\left( {\frac{y}{{\left\| {\bf{u}} \right\|}}} \right)}^2} + {{\left( {\frac{z}{{\left\| {\bf{u}} \right\|}}} \right)}^2}} = \frac{{\sqrt {{x^2} + {y^2} + {z^2}} }}{{\sqrt {{{\left\| {\bf{u}} \right\|}^2}} }} = \frac{{\bf{u}}}{{\left\| {\bf{u}} \right\|}} = 1\]

因此， \({\bf{\hat u}}\)确实是一个单位向量。

例1.3

对向量v= (−1,3,4) 进行规范化。我们计算\(\left\| {\bf{v}} \right\| = \sqrt {{{( - 1)}^2} + {3^2} + {4^2}} = \sqrt {26} \) 。则， \({\bf{\hat v}} = \frac{{\bf{v}}}{{\left\| {\bf{v}} \right\|}} = \left( { - \frac{1}{{\sqrt {26} }},\frac{3}{{\sqrt {26} }}\frac{4}{{\sqrt {26} }}} \right)\)

要验证\({\bf{\hat v}}\)是否为单位向量，只需计算它的长度：

\[\left\| {{\bf{\hat v}}} \right\| = \sqrt {{{\left( { - \frac{1}{{\sqrt {26} }}} \right)}^2} + {{\left( {\frac{3}{{\sqrt {26} }}} \right)}^2} + {{\left( {\frac{4}{{\sqrt {26} }}} \right)}^2}} = \sqrt {\frac{1}{{26}} + \frac{9}{{26}} + \frac{{16}}{{26}}} = \sqrt 1 = 1\]

发布时间：2014/9/7 下午8:57:55  阅读次数：4965