1.1 向量

计算机绘图、碰撞检测和物理模拟是现代视频游戏的基本组成部分，向量（vector）在这些领域中具有至关重要的作用。本书所采用的教学方式与普通教科书不同，我们所提供的所有的知识都是基于实践的；我们在这里为读者推荐一本专门讲解3D游戏与绘图的数学教程[Verth04]。读者在本书的每个演示程序中都会看到一些注释，我们通过这些注释来强调向量的重要性。

学习目标

1．学习使用几何与数值方式表示向量。

2．了解向量运算及向量的几何应用。

3．熟悉XNA数学中的向量函数和向量类。

向量（vector）是一种同时具有大小和方向的物理量（quantity）。同时具有大小和方向的物理量称为向量值物理量（vector-valued quantity）。常见的向量值物理量有：力（在某个特定方向上施加一定的作用力——量值），位移（在某个净方向上移动一段距离），速度（速率和方向）。因此，向量可以用来表示力、位移和速度。有时我们也用向量来表示一个单个方向，比如玩家在3D游戏中的观察方向、多边形面对的方向、光线的传播方向以及从一个物体表面折回的反射光方向。

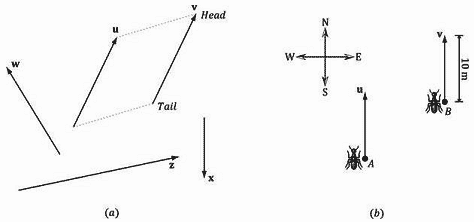
首先，我们从几何学角度描述向量的算术特征：我们通过一个有向线段来表示向量（参见图1.1），其中长度表示向量的大小，箭头表示向量的方向。我们注意到，向量所描绘的位置并不重要，改变向量的位置并不会影响向量的大小和方向（这是向量具有的两个属性）。也就是，当且仅当两个向量具有相同的长度和方向时，我们说这两个向量相等。所以，图1.1a中的两个向量u和v实际上是相等的，因为它们具有相同的长度和方向。其实，位置对于向量来说无关紧要，我们可以随便平移一个向量，但是不会改变该向量所表示的含义（因为平移即不会改变向量的长度，也不会改变向量的方向）。注意，我们可以平移u，使它与v重叠（反之亦然），由此使它们彼此难以区分——因为它们是相等的。举一个物理上的例子，图1.1b中的向量u和v表示位于不同位置上的两只蚂蚁A和B从当前位置开始向北移动10米。也就是这里的u=v。由于向量本身与位置无关；所以它们只是告诉蚂蚁该从当前位置向哪个方向移动，以及移动多远的距离。在本例中，它们告诉蚂蚁向北（方向）移动10米（长度）。

1.1.1 向量和坐标系

我们现在学习如何定义用于几何运算的向量，随后我们要用向量来解决各种向量值问题。不过，我们无法在计算机中以几何方式表示向量，我们必须寻求一种替代方案，以数字方式表示向量。所以我们在空间中引入了3D坐标系的概念，并将所有的向量尾部平移到坐标系原点（图1.2）。然后通过指定向量首部的坐标来表示一个向量，记作v= (x,y,z)，如图1.3所示。现在，我们可以在计算机程序中用3个浮点数来表示一个向量了。

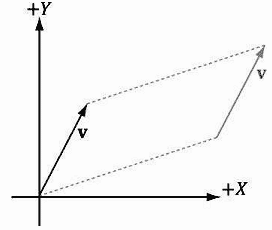
注意：若只处理2D，那么只需要使用一个2D坐标系统，向量只有两个坐标：v= (x,y)，在计算机程序中可以用2个浮点数来表示一个向量。

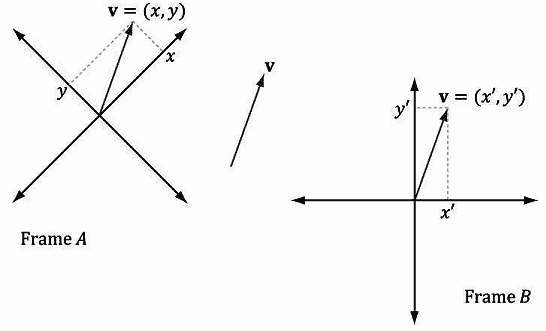
考虑图1.4，它展示了一个向量v以及空间中的两个参照系。注意，我们在本书中使用术语frame、参照系（frame of reference）、空间（space）、坐标系（coordinate system）来表示相同含义。我们平移v，使它位于两个参照系的标准位置上。可以看到，向量v相对于参照系A的坐标不同于向量v相对于参照系B的坐标。换句话说，对于不同的参照系，同一个向量会有不同的坐标。

这一概念说起来与物理学中的温度颇为相似。水的沸点是摄氏100º或华氏212º。使水沸腾的物理温度是相同的，与温标无关（即，我们不可能通过改变温标来提高或降低水的沸点），但是我们必须根据当前选用的温标来指定不同的标量值。同样，对于一个向量来说， 它的方向和大小被牢牢地固定在有向线段中，不会改变；只有在以不同的参照系描述向量时，它的坐标才会改变。这一点很重要，因为我们无论何时通过坐标来表示一个向量，这些坐标都是相对于某一参照系的。通常在3D计算机绘图中我们使用的参照系不只一个，所以必须保证向量坐标与对应的参考系一致；另外，我们需要知道如何完成从一个参照系到另一个参照系的向量坐标转换。

注意：我们看到，在一个参照系中向量和点都可以使用坐标(x,y,z)来描述。但是，它们的意义完全不同；点表示的是三维空间中的位置，而向量表示的是大小和方向。点会在随后的1.5节中讨论。

1.1.2 左手坐标系和右手坐标系

Direct3D使用所谓的左手坐标系（left-handed coordinate system）。假如你把左手手指指向x轴正方向，然后朝y轴正方向弯曲四指，大拇指就会指向z轴正方向。图1.5展示了左手坐标系和右手坐标系之间的区别。

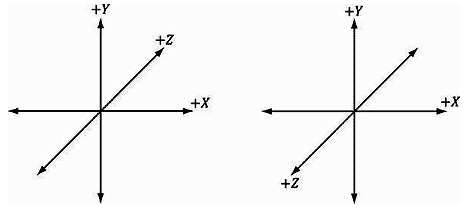
观察右手坐标系。假如你把右手手指指向x轴正方向，然后朝y轴正方向弯曲四指，大拇指就会指向z轴正方向。

1.1.3 基本向量运算

现在，我们使用坐标来描述向量的判等运算、加法运算、标量乘法运算和减法运算。我们设u=(u_x,u_y,u_z)和v=(v_x,v_y,v_z)。

1．当且仅当两个向量的各自分量相等时，这两个向量相等。也就是说，仅当u_x=v_x、u_y=v_y、u_z=v_z时，u=v。

2．两个向量的对应分量可以相加；仅当两个向量的维度相同时，向量分量加法才有意义。u+v= (u_x+v_x,u_y+v_y,u_z+v_z)。

3．标量（即，实数）可以与向量相乘，所得结果仍为向量。设k为标量，则ku=(ku_x,ku_y,ku_z)。这种向量运算称为标量乘法。

4．减法可以通过向量加法和标量乘法来表示。也就是，u−v=u+(−1•v) =u+(−v)=(u_x−v_x,u_y−v_y,u_z−v_z)。

例 1.1

设u= (1,2,3)、v= (1,2,3)、w=(3, 0, −2)、k=2。则，

1．u+w= (1, 2,3) + (3, 0, −2) = (4, 2,1)；

2．u=v；

3．u−v=u+ (−v) = (1,2,3) + (−1, −2, −3) = (0, 0,0) = 0；

4．kw=2(3, 0, −2) = (6, 0, −4)。

第3行例举了一个特殊的向量，称为零向量。零向量的所有分量均为零，它可以由0来表示。

例 1.2

我们将用个例子来解释如何使用2D向量来简化绘图操作。3D向量的原理基本相同，只是比2D向量多了一个分量而已。

1．设v= (2,1)。在几何学中v和−v/2是如何进行比较的呢？把v和−v/2同时绘制出来（图1.6a），我们注意到−v/2= (−1, −1/2)，它们的方向恰好相反，而−v/2的长度是v的一半。所以，在几何学中对向量取负值可以“反转”向量的方向，而标量乘法可以缩放向量的长度。

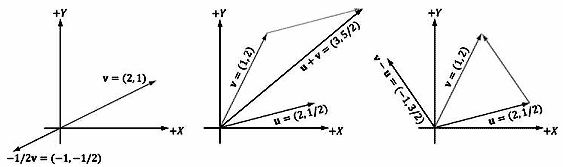
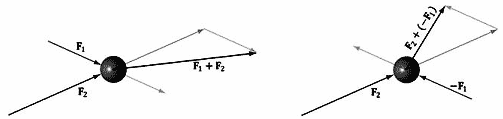
2．设u= (2,1/2)、v= (1,2)，则u+v= (3,5/2)。图1.6b描绘了向量加法在几何学中的含义：对u进行平移，使其尾部与v的首部对齐。那么，二者之和等于从v的尾部开始、到u的首部结束的向量。（如果我们保持u的位置不变，对v进行平移，使v的尾部和u的首部对齐，那么得到的结果完全相同。此时，u+v所得的向量从u的尾部开始、到平移后的v的首部结束。）另外，我们还可以看到向量加法的运算规则与我们根据自然规律从生活经验中判断出的结果一致，当我们把多个作用力加在一起时， 可以得到一个最终的净作用力：如果将同一个方向上的两个作用力（向量） 相加，那么就可以得到该方向上的一个更大的作用力（更长的向量）。如果将两个方向相反的作用力（向量）相加，那么就会得到一个较小的净作用力（较短的向量）。图1.7说明了这一概念。

3．设u=(2,1/2)、v= (1,2)，则v-u= (−1,3/2)。图1.6c说明了向量减法的几何含义。本质上，v−u得到的差值等于从u的首部开始、到v的首部结束的一个向量。如果我们把u和v视为点而不是向量，那么v−u得到的差值就等于从点u开始、到点v结束的一个向量；这种解释方式非常重要，因为我们经常需要从一点指向另一点的向量。同时我们还可以看到，当把u和v视为点时，v−u的长度就是从u到v的距离。

发布时间：2014/9/5 下午9:57:36  阅读次数：7997