19.5 地形高度

我们经常要为给定的x、z坐标计算相应的地形表面高度。该功能可用于在地形表面上放置物体，或者在稍高于地形表面的位置上放置摄像机，模拟玩家在地形中行走的效果。

高度图给出了网格顶点的地形高度。但是我们还需要顶点之间的地形高度。所以，我们必须使用插值，通过一个连续表面y=ℎ(x,z)描述地形，在离散的高度图上进行采样。由于地形是通过三角形网格来模拟的，所以线性插值在这里有意义，它可以使我们的高度函数与地形网格几何体保持一致。

要解决个问题，我们的第一步是计算x、z坐标所在的单元格。（注意：我们假设x、z坐标位于地形网格的局部空间中。）下面的代码用于完成一工作；它告诉我们x、z坐标所在的单元格的行和列。

// 从地形局部空间转换到"cell"空间.
float c = (x + 0.5f*width()) / mInfo.CellSpacing; 
float d = (z - 0.5f*depth()) / -mInfo.CellSpacing; 
// 获取所在的行和列.
int row = (int)floorf(d); 
int col = (int)floorf(c);

图19.12a和19.12b解释了这段代码的含义。从本质上讲，我们是把点变换到了一个新的坐标系中，该坐标系的原点位于网格的左上角，z轴正方向垂直向下，单位为单元格。在该坐标系中，单元格的行和列分别等于floor(z)和floor(x)，如图19.12b所示。在图例中，点位于第4行、第1列（索引从0开始）。（记住，C++函数floor(t)用于求解小于等于t的最大整数值。）另外还要注意，行号和列号是单元格左上角顶点的索引。

现在我们已知点所在的单元格，我们可以从高度图中获取该单元格的4个顶点高度：

// 获取所在单元格的4个顶点高度. 
// A*--*B
// |  / |
// |/   |
// C*--*D 
float A = mHeightmap[row*mInfo.NumCols + col]; 
float B = mHeightmap[row*mInfo.NumCols + col + 1]; 
float C = mHeightmap[(row+1)*mInfo.NumCols + col]; 
float D = mHeightmap[(row+1)*mInfo.NumCols + col + 1];

现在，我们已经知道了点所在的单元格以及单元格的4个顶点高度。下面我们需要求出地形表面在特定x、z坐标处的高度（y坐标）。这个问题有点棘手，因为单元格会沿着两个方向倾斜；参见图19.13。

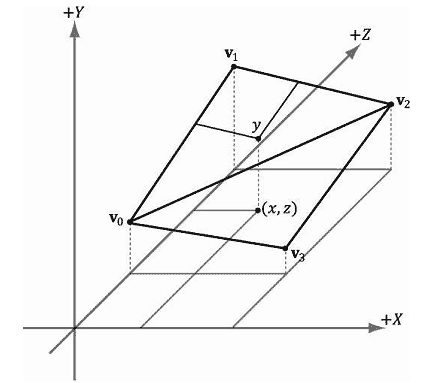
为了求出高度，我们必须知道点在单元格的哪个三角形中（记住，单元格会被分成两个三角形来进行渲染）。想要知道点位于哪个三角形，我们必须进行一次坐标变换，在单元格坐标系（参见图19.12c）中描述坐标(s,t)。该变换只包含一次简单的平移，它的代码如下：

float s=c-(float)col;
float t=d-(float)row;

那么，当s+t≤1时，点位于“上”三角形△ABC中；反之，点位于“下”三角形△DCB中。

现在我们讲解如何在“上”三角形中计算点的高度。当然，“下”三角形的计算过程基本相同，这两种情况的代码稍后会一并列出。为了求解点在“上”三角形中的高度，我们首先要创建两个向量u = (Δx, B−A ,0)和v = (0, C−A,-Δz)，这两个向量以三角形边上的端点Q为起点，如图19.14a所示。然后，我们通过s对u进行线性插值，通过t对v进行线性插值。图19.14b解释了这些插值。点Q+su+tv的y坐标就是点(x,z)在地形表面上的高度（回忆一下向量加法的几何含义有助于加深对该问题的理解）。

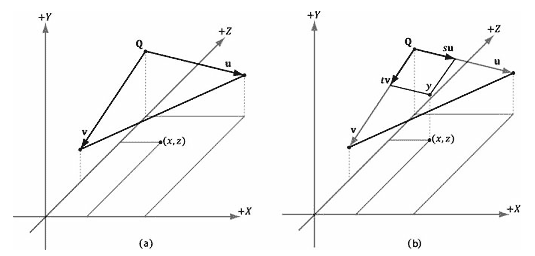
注意，由于我们只关心插值后的高度，所以可以只对y分量进行插值，忽略其他分量。这样高度的计算公式可归纳为A+su_y+tv_y。

从而，Terrain::getHeight函数的结尾部分的代码为：

// 如果是上三角形ABC.
if( s + t <= 1.0f)
{
	float uy = B - A;
	float vy = C - A;
	return A + s*uy + t*vy;
}
else // 下三角形DCB.
{
	float uy = C - D;
	float vy = B - D;
	return D + (1.0f-s)*uy + (1.0f-t)*vy;
}

现在我们就可以将相机限定在地形之上用以模拟玩家正在地形上行走的效果：

void TerrainApp::UpdateScene(float dt)
{
	//
	// 控制相机.
	//
	if( GetAsyncKeyState('W') & 0x8000 )
		mCam.Walk(10.0f*dt);

	if( GetAsyncKeyState('S') & 0x8000 )
		mCam.Walk(-10.0f*dt);

	if( GetAsyncKeyState('A') & 0x8000 )
		mCam.Strafe(-10.0f*dt);

	if( GetAsyncKeyState('D') & 0x8000 )
		mCam.Strafe(10.0f*dt);

	//
	// Walk/fly模式
	//
	if( GetAsyncKeyState('2') & 0x8000 )
		mWalkCamMode = true;
	if( GetAsyncKeyState('3') & 0x8000 )
		mWalkCamMode = false;

	// 
	// 在walk模式中，将相机限定在地形表面之上.
	//
	if( mWalkCamMode )
	{
		XMFLOAT3 camPos = mCam.GetPosition();
		float y = mTerrain.GetHeight(camPos.x, camPos.z);
		mCam.SetPosition(camPos.x, y + 2.0f, camPos.z);
	}

	mCam.UpdateViewMatrix();
}

文件下载（已下载 571 次）

发布时间：2014/8/26 下午7:13:33 阅读次数：4234

19.5 地形高度

评论