18.3 纹理/正切空间

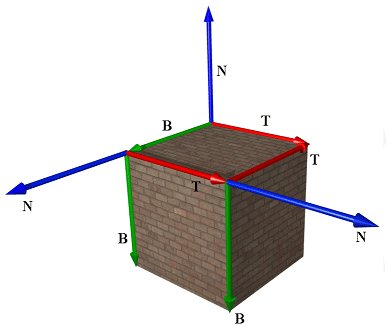
考虑一个3D纹理映射三角形。为便于讨论，我们假设在进行纹理贴图映射没有拉伸问题；也就是说，将纹理三角形映射到3D三角形的过程只是一个刚体变换过程（平移和旋转）。现在，假设纹理是一张彩色帖纸。我们对它进行平移和旋转，把它贴到3D三角形上。图18.4说明了如何在纹理坐标轴与3D三角形之间建立联系：它们正切于三角形，并位于三角形平面上。当然，三角形的纹理坐标是相对于纹理坐标系的。现在把三角形平面法线N合并进来，我们便得到了一个在三角形平面上的3D TBN基（3D TBN-basis），我们将它称为纹理空间（texture space）或正切空间（tangent space）。注意，正切空间通常会随着三角形而变化（参见图18.5）。

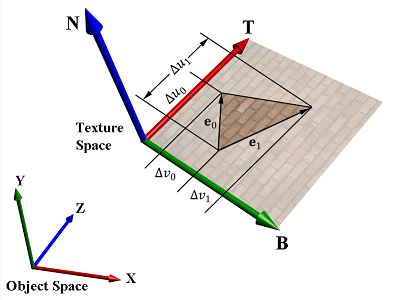
如图18.3所示，我们存储在法线贴图中的法线向量使用的是纹理空间坐标系。而场景中的光照使用的是世界空间坐标系。为了进行光照，我们必须把法线向量和灯光变换到同一个坐标系中。那么我们的第一步是要在正切空间坐标系和三角形顶点的物体空间坐标系之间建立联系。只要进入物体空间，我们就可以通过世界矩阵实现从物体空间到世界空间的坐标变换（具体实现过程在下一节讲解）。现在，我们设v₀、v₁、v₂为3D三角形的3个顶点，对应的纹理坐标为(u₀,v₀)、(u_1,v₁)、(u₂,v₂)，这些纹理坐标定义了纹理坐标轴（即，T和B）上的纹理三角形。设e₀=v₁ – v₀、e₁= v₂− v₀为3D三角形的两个边向量，对应的纹理三角形的边向量为(Δu₀,∆v₀) = (u₁ – u₀,v₁ – v₀)、(Δu₁,∆v₁) = (u₂ – u₀,v₂ – v₀)。从图18.4中可以看出：

\[\begin{array}{l}{{\bf{e}}_0} = \Delta {u_0}{\bf{T}} + \Delta {v_0}{\bf{B}}\\{{\bf{e}}_1} = \Delta {u_1}{\bf{T}} + \Delta {v_1}{\bf{B}}\end{array}\]

使用相对于物体空间的坐标表示向量，可以得到矩阵方程：

\[\left[ \begin{array}{l}\begin{array}{*{20}{c}}{{e_{0,x}}}&{{e_{0,y}}}&{{e_{0,z}}}\end{array}\\\begin{array}{*{20}{c}}{{e_{1,x}}}&{{e_{1,y}}}&{{e_{1,z}}}\end{array}\end{array} \right] = \left[ {\begin{array}{*{20}{c}}{\Delta {u_0}}&{\Delta {v_0}}\\{\Delta {u_1}}&{\Delta {v_1}}\end{array}} \right]\left[ \begin{array}{l}\begin{array}{*{20}{c}}{{T_x}}&{{T_y}}&{{T_z}}\end{array}\\\begin{array}{*{20}{c}}{{B_x}}&{{B_y}}&{{B_z}}\end{array}\end{array} \right]\]

注意，只要我们知道三角形顶点的物体空间坐标，那么就等于知道了边向量的物体空间坐标。所以矩阵

\[\left[ \begin{array}{l}\begin{array}{*{20}{c}}{{e_{0,x}}}&{{e_{0,y}}}&{{e_{0,z}}}\end{array}\\\begin{array}{*{20}{c}}{{e_{1,x}}}&{{e_{1,y}}}&{{e_{1,z}}}\end{array}\end{array} \right]\]

 是已知的。同样，我们知道纹理坐标，所以矩阵

\[\left[ {\begin{array}{*{20}{c}}{\Delta {u_0}}&{\Delta {v_0}}\\{\Delta {u_1}}&{\Delta {v_1}}\end{array}} \right]\]

 是已知的。

求解T和B的物体空间坐标：

\[\begin{array}{l}\left[ \begin{array}{l}\begin{array}{*{20}{c}}{{T_x}}&{{T_y}}&{{T_z}}\end{array}\\\begin{array}{*{20}{c}}{{B_x}}&{{B_y}}&{{B_z}}\end{array}\end{array} \right] = {\left[ {\begin{array}{*{20}{c}}{\Delta {u_0}}&{\Delta {v_0}}\\{\Delta {u_1}}&{\Delta {v_1}}\end{array}} \right]^{ - 1}}\left[ \begin{array}{l}\begin{array}{*{20}{c}}{{e_{0,x}}}&{{e_{0,y}}}&{{e_{0,z}}}\end{array}\\\begin{array}{*{20}{c}}{{e_{1,x}}}&{{e_{1,y}}}&{{e_{1,z}}}\end{array}\end{array} \right]\\ = \frac{1}{{\Delta {u_0}\Delta v{}_1 - \Delta {v_0}\Delta {u_1}}}\left[ {\begin{array}{*{20}{c}}{\Delta {v_1}}&{ - \Delta {v_0}}\\{ - \Delta {u_1}}&{\Delta {u_0}}\end{array}} \right]\left[ \begin{array}{l}\begin{array}{*{20}{c}}{{e_{0,x}}}&{{e_{0,y}}}&{{e_{0,z}}}\end{array}\\\begin{array}{*{20}{c}}{{e_{1,x}}}&{{e_{1,y}}}&{{e_{1,z}}}\end{array}\end{array} \right]\end{array}\]

我们在上述方程中使用了一个逆矩阵运算的推论，即给定一个矩阵\({\bf{A}} = \left[ {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right]\)，可有：

\[{{\bf{A}}^{{\rm{ - }}1}} = \frac{1}{{ad - bc}}\left[ {\begin{array}{*{20}{c}}d&{ - b}\\{ - c}&a\end{array}} \right]\]

注意，物体空间中的向量T和B通常不是单位向量，而且当纹理出现拉伸问题时，它们彼此并不垂直。

T、B、N向量分别称为切线向量、副法线向量（或副切线向量）、法线向量。

发布时间：2014/8/22 下午7:44:05  阅读次数：5049