11.1 几何着色器编程

若我们不使用曲面细分阶段，则几何着色器（geometry shader）阶段是一个可选阶段，它位于顶点着色器和像素着色器阶段之间。顶点着色器以顶点作为输入数据，而几何着色器以完整的图元作为输入数据。例如，当我们绘制三角形列表时，几何着色器处理的是列表中的每个三角形T：

for(UINT i = 0; i < numTriangles; ++i)
    OutputPrimitiveList = GeometryShader(T[i].vertexList);

注意，这里是将每个三角形的3个顶点作为几何着色器的输入数据，几何着色器的输出为图元列表。顶点着色器无法创建或销毁顶点，而几何着色器的主要优点就是它可以创建或销毁几何体；这样就可以在GPU上实现一些有趣的效果。例如，几何着色器可以将输入图元扩展为一个或多个其他图元，或者根据一些条件屏蔽某些图元的输出。注意，输出图元可以与输入图元的类型不同；例如，几何着色器的常见用途是将一个点扩展为一个四边形（即，两个三角形）。

几何着色器的输出图元由一个顶点列表来描述。在顶点离开几何着色器之前，顶点坐标必须变换到齐次裁剪空间。在几何着色器阶段之后，顶点列表描述的是齐次裁剪空间中的图元。与往常一样，这些顶点会被投影（齐次除法），随后进行光栅化处理。

学习目标

学习如何编写几何着色器。
理解如何使用几何着色器实现高效的广告牌算法。
了解自动生成的图元ID以及它的一些用途。
学习如何创建和使用纹理数组，以及纹理数组的一些用途。
理解alpha-to-coverage是如何改进alpha剪裁中的锯齿问题的。

几何着色器编程与顶点/像素着色器编程非常相似，只是略有一些差异。下面的代码展示了它的一般格式：

[maxvertexcount(N)] 
void ShaderName (
    PrimitiveType InputVertexType InputName [NumElements], 
    inout StreamOutputObject<OutputVertexType>OutputName) 
{ 
    // Geometry shader body... 
}

首先，我们必须指定每次调用几何着色器时所能输出的顶点的最大数量。这一工作通过在着色器定义之前指定maxvertexcount属性来实现：

[maxvertexcount(N)]

其中，N是每次调用几何着色器时所能输出的顶点的最大数量。几何着色器每次输出的顶点数量都可以不同，只要不超过指定的最大值就没问题。从性能方面考虑，maxvertexcount应尽可能小，[NVIDIA08]指出当GS的输出介于1-20个标量之间时性能最佳，在27-40个标量之间则性能损失50%。每次调用输出的标量大小是指maxvertexcount的生成和在输出顶点类型结构中的标量数量。有了这个限定，实际工作会非常困难，你要么接受性能的损失，要么选择不使用几何着色器而用别的方法代替；但是，我们必须要考虑到别的方法也会有缺点，可能几何着色器反而是个较好的选择。而且，[NVIDIA08]中的推荐设置发表于2008（几何着色器第一次发布），所以现在可能已经改进过了。

几何着色器有两个参数：一个输入参数和一个输出参数。（其实，它的参数不只两个，我们会在后面的11.2.4节专门讨论个话题。）输入参数总是一个顶点数组，它可以表示：单个顶点、由两个顶点构成的直线、由3个顶点构成的三角形、由4个顶点构成的带有邻接信息的直线、由6个顶点构成的带有邻接信息的三角形。输入的顶点类型与顶点着色器返回的顶点类型相同（例如，VertexOut）。输入参数必须加上一个图元类型前缀，描述将要输入到几何着色器的图元类型。可以使用的图元类型包括：

1．point：输入图元为点。

2．line：输入图元为直线（列表或线带）。

3．triangle：输入图元为三角形（列表或线带）。

4．lineadj：输入图元为带有邻接信息的直线（列表或线带）。

5．triangleadj：输入图元为带有邻接信息的三角形（列表或线带）。

注意：几何着色器的输入图元总是一个完整的图元（例如，由两个顶点构成一条直线、由三个顶点构成一个三角形）。这样，几何着色器就不需要区分列表和线带了。例如，在绘制三角形线带时，几何着色器会处理线带中的每个三角形，而且每个三角形的3个顶点都会作为输入数据传入到几何着色器中。这会导致额外的工作，因为几何着色器会重复处理被多个图元共享的顶点。

输出参数总是带有inout修饰符，并且是一个流类型（stream type）对象。流类型用于存储由几何着色器输出的几何体顶点列表。几何着色器使用内置的Append方法向输出流添加顶点：

 void StreamOutputObject<Outputvertextype>::Append(OutputVertexType v);

流类型是一种模板类型（template type），其中的模板参数用于指定输出顶点的类型（例如，GeoOUT）。这里有3种可以使用的流类型：

1．PointStream<OutputVertexType>：描述单个点的顶点列表。

2．LineStream<OutputVertexType>：描述直线线带的顶点列表。

3．TriangleStream<OutputVertexType>：描述三角形线带的顶点列表。

几何着色器以图元为单位输出顶点；输出图元的类型由流类型（PointStream、LineStream、TriangleStream）决定。对于直线和三角形来说，输出图元总是一个线带。不过，我们也可使用内置的RestartStrip方法模拟输出直线列表和三角形列表：

 void StreamOutputObject<Outputvertextype>::RestartStrip();

例如，当你希望输出一个三角形列表时，你应该每输出3个顶点，调用一次RestartStrip方法（也就是，在每调用3次Append 方法之后，调用一次RestartStrip方法）。下面是一些几何着色器签名的例子：

// 例1: GS最多输出4个顶点。输入图元为一条线，输出为一个三角形线带。
// 
[maxvertexcount(4)] 
void GS(line VertexOutT gin[2],
    inout TriangleStream<GeoOut> triStream) 
{ 
    // Geometry shader body... 
} 
// 
// EXAMPLE 2: GS outputs at most 32 vertices.The input primitive is a triangle. The output is a triangle strip. 
// 
[maxvertexcount(32)] 
void GS(triangle VertexOut gin[3], 
inout TriangleStream<GeoOut> triStream) 
{ 
    // Geometry shader body... 
} 
// 
// EXAMPLE 3: GS outputs at most 4 vertices. The input primitive 
// is a point. The output is a triangle strip. 
// 
[maxvertexcount(4)] 
void GS(point VertexOut gin[1], 
inout TriangleStream<GeoOut> triStream) 
{ 
    // Geometry shader body... 
}

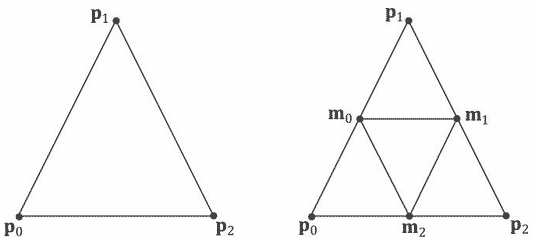
下面的几何着色器解释了Append和RestartStrip方法的用法；它输入一个三角形，对它进行细分（参见图11.1），并输出4个细分后的三角形：

struct VertexOut 
{ 
    float3 posL      : POSITION; 
    float3 normalL : NORMAL; 
    float2 Tex : TEXCOORD; 
}; 
struct GeoOut 
{ 
     loat4 posH      : SV_POSITION; 
    float3 posW      : POSITION; 
    float3 normalW : NORMAL; 
    float2 Tex       : TEXCOORD;
    float FogLerp   :  FOG;
}

void  Subdivide (VertexOut inVerts[3], out VertexOut outVerts[6])
{
    //        1 
    //        * 
    //       /  \ 
    //      /    \ 
    //    m0*-----*m1 
    //    / \    / \ 
    //   /   \  /   \ 
    //  *-----*-----* 
    // 0      m2      2 

    VertexOut  m[3];
    // 计算每条边的中点
    m[0].PosL = 0.5f*(inVerts[0].PosL+inVerts[1].PosL);
    m[1].PosL  = 0.5f*(inVerts[1].PosL+inVerts[2].PosL);
    m[2].PosL = 0.5f*(inVerts[2].PosL+inVerts[0].PosL);
    // 投影到一个单位圆上
    m[0].PosL = normalize(m[0].PosL);
    m[1].PosL = normalize(m[1].PosL);
    m[2].PosL  = normalize(m[2].PosL);
    //  求得法线
    m[0].NormalL = m[0]. Pos L;
    m[1].NormalL  = m[1]. Pos L;
    m[2].NormalL  = m[2]. Pos L;
    // 插值求得纹理坐标
    m[0].Tex =  0.5f*(inVerts[0].Tex+inVerts[1].Tex);
    m[1].Tex =  0.5f*(inVerts[1].Tex+inVerts[2].Tex);
    m[2].Tex =  0.5f*(inVerts[2].Tex+inVerts[0].Tex);
    outVerts[0] = inVerts[0];
    outVerts[1] = m[0];
    outVerts[2] = m[2];
    outVerts[3] = m[1];
    outVerts[4] = inVerts[2];
    outVerts[5] = inVerts[1];
} ;

void OutputSubdivision(VertexOut v[6],inout TriangleStream<GeoOut>  triStream)
{
    GeoOut gout[6];
    [unroll]
    for(int i = 0; i  < 6; ++i)
    {
        // 转换到世界空间
        gout[i].PosW = mul(float4(v[i].PosL,1.0f), gWorld).xyz;
        gout[i].NormalW = mul(v[i].NormalL,(float3x3)gWorldInvT ranspose);
        // 转换到齐次剪裁空间
        gout[i].PosH = mul(float4(v[i].PosL,1.0f), gWorldViewProj);
        gout[i].Tex = v[i].Tex;
    }
    //        1 
    //        * 
    //       /  \ 
    //      /    \ 
    //    m0*-----*m1 
    //    / \    / \ 
    //   /   \  /   \ 
    //  *-----*-----* 
    // 0      m2      2 

    //  我们可以使用两个线带绘制细分三角形:
    //  第一个：底部的三个三角形
    //  第二个:顶部的一个三角形
     [unroll]
    for(int  j   =  0;  j   <  5;  ++j )
    {
        triStream.Append(gout[j]);
    }
    triStream.RestartStrip();
    triStream.Append(gout[1]);
    triStream.Append(gout[5]);
    triStream.Append(gout[3]);
}

[maxvertexcount(8)]
void GS(triangle VertexOut gin[3], inout TriangleStream<GeoOut>)
{
    VertexOut v[6];
    Subdivide(gin,v);
    OutputSubdivision(v, triStream);
}

注意：给定一个输入图元，几何着色器可以不对它进行输出。通过这一方式，几何着色器可以将输入的几何体“销毁”，这一功能在某些算法中非常有用。

注意：当几何着色器输出的顶点无法构成一个完整的图元时，这部分图元将被丢弃。

文件下载（已下载 1145 次）

发布时间：2014/8/14 下午9:33:26 阅读次数：7014

11.1 几何着色器编程

评论