7.11 聚光灯

在现实生活中，最常见的聚光灯是手电筒。本质上，聚光灯由一个位置Q、一个方向向量d和一个圆锥体光照区域来描述（参见图7.20）。

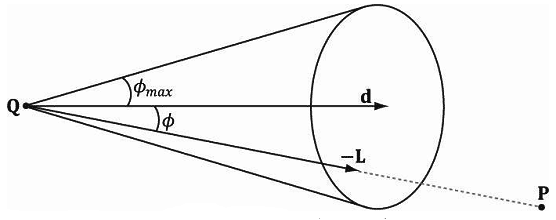
当实现一个聚光灯时，我们开始所做的事情与点光相同。光照向量可以由以下公式描述： 其中，P是接收照的点的位置，Q是聚光灯的位置。从图7.20中可以看到，当且仅当， −L与d之间的角度ϕ小于圆锥角ϕm_ax时，P在聚光灯的锥形范围内（所以它可以接收光照）。另外，在聚光灯的圆锥体区域中的线应该具有不同的强度；越靠近圆锥体中心的光线应该越强，随着角度ϕ从0增加到ϕ_max，光线强度应该逐渐衰退为0（零）。

那么，我们应该如何通过一个ϕ的函数来控制衰减强度，以及如何控制聚光灯的圆锥体区域大小呢？其实很简单，我们只需要故伎重演，直接套用控制镜面高光圆锥体反射系数的公式即可。也就是，使用如下函数：

\({k_{spot}}(\phi ) = \max {(\cos \phi ,0)^s} = \max {( - {\bf{L}} \cdot {\bf{d}},0)^s}\)

回顾图7.12所示的函数曲线图。我们可以看到，当ϕ增加时，强度逐渐衰减，这是我们想要得到的结果；另外，通过修改指数s，我们可以间接地控制ϕ_max（它是当光照强度降低为0时的圆锥体角度）；也就是说，我们可以通过改变s来缩小或扩大聚光灯的圆锥体区域大小。例如，当我们将s设为8时，圆锥体的半角角度约为45º。这样，聚光灯与点光的方程基本相同，只是要再乘以一个聚光灯因子，根据点与聚光灯圆锥体的相对位置按比例调整光照强度：

\(LitColor = {k_{spot}}({\bf{A}} + \frac{{{k_d}{\bf{D}} + {k_s}{\bf{S}}}}{{{a_0} + {a_1}d + {a_2}{d^2}}})\)（公式7.5）

注意：比较公式7.4和7.5，我们可以看出聚光灯比点光耗费的资源要高得多，这是因为我们需要计算k_spot因子。同理，比较公式7.3和7.4，我们可以看出点光比平行光耗费的资源要高得多，这是因为需要计算距离d（这个计算涉及到平方根运算，非常耗时），而且需要除以衰减表达式。总而言之，从资源耗费角度而言，平行光要求最低，点光其次，聚光灯最高。

发布时间：2014/8/6 下午2:33:24  阅读次数：4555