7.6 镜面光

考虑图7.11所示的光滑表面。当灯照射在这样一个表面上时，光线会在一个由反射系数描述的圆锥体区域内形成锐利的反射；我们将这种反射称为镜面高光反射（specular reflection，或直译为镜面反射）。与漫反射不同，高光可能不会传入眼睛，因为它只在一个特定的方向上反射；高光的计算过程与观察点的位置相关。也就是说，当场景中的观察点位置发生变化时，我们看到的高光强度也会跟着变化。

镜面反射的圆锥体区域由一个反射向量r和一个角度ϕ_max来定义。简单来说，反射光的强度可由反射向量r和观察向量v=\(\frac{{{\bf{E}}{\rm{ - }}{\bf{P}}}}{{\left\| {{\bf{E}} - {\bf{P}}} \right\|}}\) （即，从表面点P到观察点位置E的单位向量）之间的夹角ϕ来决定。我们约定：当ϕ =0时，高光强度最大；当ϕ逐渐接近于时，高光强度逐渐降低为0。为了以数学方式来描述一过程，我们需要对使用兰伯特余弦定理的函数做一些修改。图7.12说明了使用不同幂时的余弦函数曲线图，其中p≥1。本质上，通过为p指定不同的值，我们可以间接地控制当高光强度降低为0时的圆锥体角度ϕ_max。参数p可以用来控制表面的平滑程度；也就是，非常精细的表面比缺乏光泽的表面的反射系数小（反射光更锐利）。所以，我们应该为光滑表面指定一个比不光滑表面更大的p值。

注意，因为v和r是单位向量，所以cosϕ = v•r。

我们现在定义照模型中的高光项：

c_s = k_s•l_s ⨂ m_s = ksS

其中

\({k_s} = \left\{ {\begin{array}{*{20}{c}}{\max {{({\bf{v}} \cdot {\bf{r}},0)}^P},{\bf{L}} \cdot {\bf{n}} > 0}\\{0,{\bf{L}} \cdot {\bf{n}} \le 0}\end{array}} \right.\)

颜色l_s指定了光源发出的高光总量。镜面材质颜色m_s指定了表面反射和吸收的入射高光总量。系数k_s根据r和v之间的夹角来决定高光强度。图7.13说明了一个表面可能接收不到漫反射光（L•n <0），但是却可以接收到高光。不过，在这种情况下，它收到的高光是毫无意义的，我们应该将k_s设为0。

注意：高光幂p的取值应该总是大于1的。

新的光照模型为：

LitColor = l_a⨂m_a + k_d•l_d ⨂ m_d + k_s•l_s ⨂ m_s = A + k_dD + ksS （公式7.3）

k_d = max(L∙n ,0)

\({k_s} = \left\{ {\begin{array}{*{20}{c}}{\max {{({\bf{v}} \cdot {\bf{r}},0)}^P},{\bf{L}} \cdot {\bf{n}} > 0}\\{0,{\bf{L}} \cdot {\bf{n}} \le 0}\end{array}} \right.\)

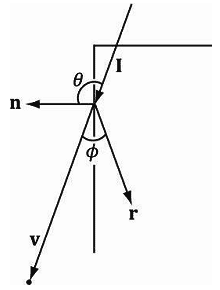
注意：反射向量r = I − 2(n•I)n（参见图7.14）。（这里假设n是一个单位向量。）不过，我们在着色器程序中总是使用HLSL的内置函数reflect来计算。这里的入射光向量I是指入射光的方向（它与光线向量L的方向相反） 。

发布时间：2014/8/5 下午8:48:53  阅读次数：5108