7.2 法线向量
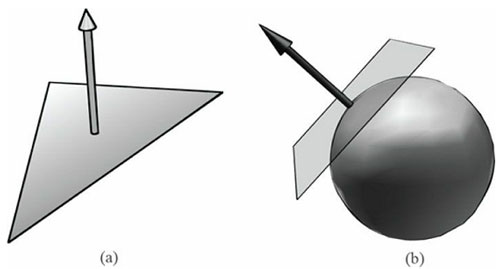
平面法线(face normal)是描述多边形所朝方向的单位向量(即,它与多边形上的所有点相互垂直),如图7.4a所示。表面法线(surface normal)是与物体表面上的点的正切平面(tangent plane)相互垂直的单位向量,如图7.4b所示。表面法线确定了表面上的点“面对”的方向。
当进行光照计算时,我们必须为三角形网格表面上的每个点求解表面法线,以确定光线与网格表面在该点位置上的入射角度。为了获得表面法线,我们必须为每个顶点指定表面法线(这些法线称为顶点法线)。然后在光栅化阶段,这些顶点法线会在三角形表面上进行线性插值,使三角形表面上的每个点都获得一个表面法线(回顾5.10.3节并参见图7.5)。
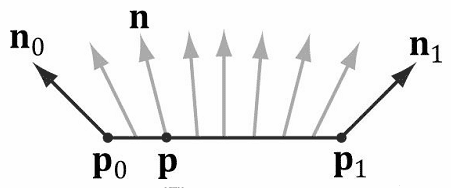
注意:对每个像素的法线进行插值,并进行光照计算称为逐像素光照或phong光照。还有一种负担较轻,但不够精确的方法是对每个顶点进行光照运算,称为逐顶点光照,计算结果是从顶点着色器中输出的,在像素着色器中进行插值。将计算从像素着色器转移到顶点着色器是一种常见的性能优化措施,而且在很多情况下的视觉表现与逐像素光照差别不大。
7.2.1 计算法线向量
为了求解一个三角形Δp0p1p2的平面法线,我们必须先计算该三角形边上的两个向量:
u = p1− p0
v = p2− p0
然后求得平面法线为:
\({\bf{n}} = \frac{{{\bf{u}} \times {\bf{v}}}}{{\left\| {{\bf{u}} \times {\bf{v}}} \right\|}}\)
下面的函数可以根据三角形的3个顶点来计算三角形正面(参见5.10.2节)的平面法线。
void ComputeNormal(const XMVector3& p0,
const XMVector3& p1,
const XMVector3& p2,
XMVector3& out)
{
XMVector3 u = p1 - p0;
XMVector3 v = p2 - p0;
XMVector3Cross(&out, &u, &v);
XMVector3Normalize (&out, &out);
}
对于一个微分曲面来说,我们可以使用微积分计算曲面上的点的法线。但遗憾的是,三角形网格不是微分曲面。我们通常使用一种称为顶点法线平均值(vertex normal averaging)的技术求解三角形网格上的顶点法线。对于网格上的任意顶点v来说,v的顶点法线n等于以v为共享顶点的每个多边形的平面法线的平均值。例如在图7.6中,网格上的四个多边形共享顶点v;所以,v的顶点法线为:
\({{\bf{n}}_{avg}} = \frac{{{{\bf{n}}_0} + {{\bf{n}}_1} + {{\bf{n}}_2} + {{\bf{n}}_3}}}{{\left\| {{{\bf{n}}_0} + {{\bf{n}}_1} + {{\bf{n}}_2} + {{\bf{n}}_3}} \right\|}}\)
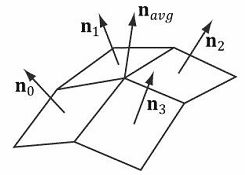
在上面的例子中,我们不需要除以4,因为我们想要的是一个普通平均值,我们可以对结果进行规范化。注意,我们还可以构造更巧妙的平均值计算公式;例如,以每个多边形的面积作为权值,计算加权平均值(这样,面积较大的多边形会占有较大的权重,而面积较小的多边形会占有较小的权重)。
下面的伪代码说明了在给出一个三角形网格的顶点列表和索引列表时,如何计算该平均值:
// 输入:
// 1.一个顶点数组(mVertices),每个顶点都有一个位置分量(pos)和
// 一个法线分量(normal).
// 2.一个索引数组(mIndices)。
// 处理网格中的每个三角形:
for(DWORD i = 0; i < mNumTriangles; ++i)
{
// 第i个三角形的索引
UNIT i0 = mIndices[i*3+0];
UNIT i1 = mIndices[i*3+1];
UNIT i2 = mIndices[i*3+2];
// 第i个三角形的顶点
Vertex v0 = mVertices[i0];
Vertex v1 = mVertices[i1];
Vertex v2 = mVertices[i2];
// 计算面法线
Vector3 e0 = v1.pos - v0.pos;
Vector3 e1 = v2.pos - v0.pos;
Vector3 faceNormal Cross( &e0, &e1);
// 这个三角形共享了以下三个顶点,
// 所以要将面法线加入到这些顶点法线的平均值中。
mVertices[i0].normal += faceNormal;
mVertices[i1].normal += faceNormal;
mVertices[i2].normal += faceNormal;
}
// 对每个顶点v,我们已经将共享v的所有三角形的面法线相加了,
// 所以现在只需归一化即可。
for(UNIT i = 0; i < mNumVertices; ++i)
mVertices[i].normal = Normalize(&mVertices[i].normal));
7.2.2 对法线向量进行变换
在图7.7a中,正切向量u = v1− v0垂直于法线向量n。当我们对这两个向量应用一个不成比例的缩放变换A时,我们可以从图7.7b中看到,变换之后的切线向量uA = v1A – v0A不再垂直于变换之后的法线向量nA。
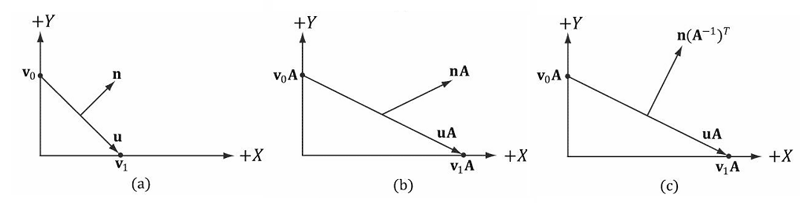
所以我们的问题是:当给出一个用于变换点和(非法线)向量的变换矩阵A时,如何求出一个专门用来变换法线向量的变换矩阵B,使变换之后的切线向量和法线向量依然保持垂直关系(即uA•uB = 0)。要解决一问题,让我们先从一些已知条件开始:我们知道法线向量n直于切线向量u。
| u•v = 0 | 切线向量垂直于法线向量 |
| unT = 0 | 用矩阵乘法来表示点积 |
| u (AA-1) nT= 0 | 插入单位矩阵I = AA-1 |
| (uA)( A-1nT ) = 0 | 矩阵乘法的结合性 |
| (uA)((A-1nT)T)T = 0 | 转置特性(AT)T = A |
| (uA)(n(A-1)T)T= 0 | 转置特性(AB)T = BTAT |
| uA•n(A-1)T = 0 | 用点积来表示矩阵乘法 |
| uA•nB = 0 | 变换之后的切线向量垂直于变换之后的法线向量 |
这样,使用B = (A-1)T(A的逆转置矩阵)来变换法线向量,就可以使它与变换之后的切线向量依然保持垂直关系。注意,当变换矩阵为正交矩阵(AT = A-1)时,B = (A-1)T = (AT)T = A;也就是,我们不必计算逆转置矩阵,直接用A来代替B即可。总之,当以一个非等比变换矩阵对法线向量进行变换时,我们必须使用该矩阵的逆转置矩阵。
在MathHelper.h中有一个辅助方法用于计算逆转置矩阵:
static XMMATRIX InverseTranspose(CXMMATRIX M)
{
// 逆转置矩阵仅用于法线。所以将矩阵中的平移行
// 设置为0,这样就不会影响逆转置矩阵的计算——因为我们
// 不需要对平移进行逆转置运算。
XMMATRIX A = M;
A.r[3] = XMVectorSet(0.0f, 0.0f, 0.0f, 1.0f);
XMVECTOR det = XMMatrixDeterminant(A);
return XMMatrixTranspose(XMMatrixInverse(&det, A));
}
因为逆转置只用于变换矢量,而平移是作用在点上的,因此需要从矩阵中排除平移因素。但是,3.2.1节告诉我们,为了防止矢量被平移操作影响,它的w应设置为0(使用齐次坐标)。因此,我们无须将矩阵中的平移行归零。但问题是,如果我们将逆转置矩阵和另一个不包含非等比例缩放的矩阵相乘,例如视矩阵(A-1 )TV,转置后位于(A-1)T第4列的平移项导致结果错误。所以,我们将平移项清零就是为了预防这个错误。正确的方法是使用((AV)-1)T对法线进行变换。下面是一个缩放和平移矩阵的例子,第4列经过逆转置后并不是[0,0,0,1]T:
\({\bf{A}} = \left( {\begin{array}{*{20}{c}}1&0&0&0\\0&{0.5}&0&0\\0&0&{0.5}&0\\1&1&1&1\end{array}} \right)\)
\({({{\bf{A}}^{ - 1}})^T} = \left( {\begin{array}{*{20}{c}}1&0&0&{ - 1}\\0&2&0&{ - 2}\\0&0&2&{ - 2}\\0&0&0&1\end{array}} \right)\)
注意:即使使用逆转置变换,法线向量也有可能会失去单位长度;所以,在变换之后必须重新规范化法线向量。
文件下载(已下载 1663 次)发布时间:2014/8/4 下午7:34:33 阅读次数:13516
