5.9 裁剪阶段

我们必须完全丢弃在平截头体之外的几何体，裁剪与平截头体边界相交的几何体，只留下平截头体内的部分；图 5.27以2D形式说明了一概念。

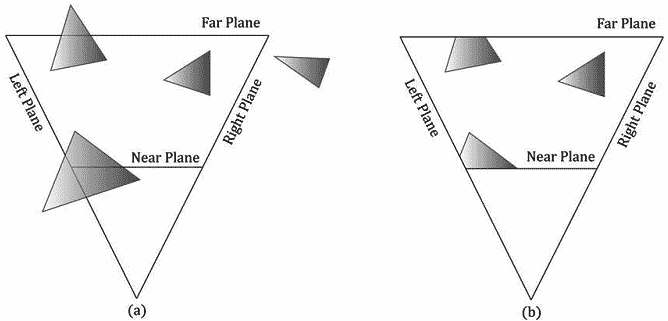
我们可以将平截头体视为由6个平面界定的空间范围：顶、底、左、右、近、远平面。要裁剪与平截头体方向相反的多边形，其实就是逐个裁剪与每个平截头体平面方向相反的多边形，当裁剪一个与平面方向相反的多边形时（参见图5.28），我们将保留平面正半空间中的部分，而丢弃平面负半空间中的部分。对一个与平面方向相反的凸多边形进行裁剪，得到的结果仍然会是一个凸多边形。由于硬件会自动完成所有的裁剪工作，所以我们不在这里讲解具体的实现细节；有兴趣的读者可以参阅[Sutherland74]，了解一下目前流行的Sutherland-Hodgeman裁剪算法。它基本思路是：求出平面与多边形边之间的交点，然后对顶点进行排序，形成新的裁剪后的多边形。

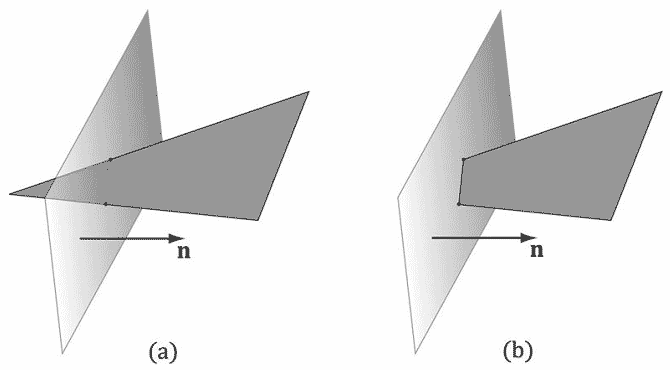
[Blinn78]描述了如何在4D齐次空间中实现裁剪算法（图5.29）。在透视除法之后，平截头体内的点(x/w, y/w, z/w ,1)将位于规范化设备空间，它的边界如下：

−1 ≤ x/w ≤ 1

−1 ≤ y/w ≤ 1

0 ≤ z/w ≤ 1

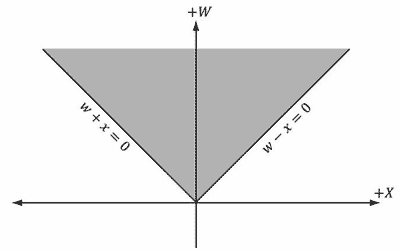
那么在透视除法之前，平截头体内的4D点(x , y , z , w)在齐次裁剪空间中的边界为：

−w ≤ x ≤ w

−w ≤ y ≤ w

0 ≤ z ≤ w

也就是，顶点被限定在以下4D平面构成的空间范围内：

左：w = −x

右：w = x

底：w = −y

顶：w = y

近：z = 0

远：z = w

只要我们知道齐次剪裁空间中的平截头体平面方程，我们就能使用任何一种裁剪算法（比如Sutherland-Hodgeman）。注意，由线段/平面相交测试的数学推论可知，这个测试在ℝ⁴也能使用，所以我们可以在齐次裁剪空间中进行4D点和4D平面的相交测试。

发布时间：2014/7/29 上午8:21:12  阅读次数：5270