5.5 输入装配阶段

5.5.1 顶点
5.5.2 图元拓扑
5.5.3 索引

输入装配（Input Assembler，简称IA）阶段从内存读取几何数据（顶点和索引）并将这些数据组合为几何图元（例如，三角形、直线）。（索引将在随后的小节中讲解。简单地说，索引规定了顶点的组织形式，解释了该以何种方式组成图元。）

5.5.1 顶点

从数学上讲，三角形的顶点位于两条边相交的位置上；而直线的顶点是端点。对于一个单个点来说，点本身就是顶点。图5.12说明了顶点的几何图形。

图5.12说明顶点只是几何图元中的一个特殊的点。不过，在Direct3D中，顶点具有更多含义。本质上，Direct3D中的顶点由空间位置和各种附加属性组成；例如，在第7章中，我们会在顶点中添加法线向量实现光照，在第8章中，在顶点中添加纹理坐标实现纹理。Direct3D可以让我们灵活地建立属于我们自己的顶点格式（例如，允许我们定义顶点的分量）。在本书中，我们会基于要绘制的效果定义一些不同的顶点格式。

5.5.2 图元拓扑

顶点是以一个叫做顶点缓冲区的Direct3D数据结构的形式绑定到图形管线的。顶点缓冲区只是在连续的内存中存储了一个顶点列表。它并没有说明以何种方式组织顶点，形成几何图元。例如，是应该把顶点缓冲区中的每两个顶点解释为一条直线，还是应该把顶点缓冲区中的每三个顶点解释为一个三角形？我们通过指定图元拓扑来告诉Direct3D以何种方式组成几何图元：

void ID3D11Device::IASetPrimitiveTopology(
    D3D11_PRIMITIVE_TOPOLOGY Topology); 

typedef enum D3D11_PRIMITIVE_TOPOLOGY 
{ 
    D3D11_PRIMITIVE_TOPOLOGY_UNDEFINED = 0, 
    D3D11_PRIMITIVE_TOPOLOGY_POINTLIST = 1, 
    D3D11_PRIMITIVE_TOPOLOGY_LINELIST = 2, 
    D3D11_PRIMITIVE_TOPOLOGY_LINESTRIP = 3, 
    D3D11_PRIMITIVE_TOPOLOGY_TRIANGLELIST = 4, 
    D3D11_PRIMITIVE_TOPOLOGY_TRIANGLESTRIP = 5, 
    D3D11_PRIMITIVE_TOPOLOGY_LINELIST_ADJ = 10, 
    D3D11_PRIMITIVE_TOPOLOGY_LINESTRIP_ADJ = 11, 
    D3D11_PRIMITIVE_TOPOLOGY_TRIANGLELIST_ADJ = 12, 
    D3D11_PRIMITIVE_TOPOLOGY_TRIANGLESTRIP_ADJ= 13, 
    D3D11_PRIMITIVE_TOPOLOGY_1_CONTROL_POINT_PATCHLIST = 33,
    D3D11_PRIMITIVE_TOPOLOGY_2_CONTROL_POINT_PATCHLIST = 34,
    .
    .
    .
    D3D11_PRIMITIVE_TOPOLOGY_32_CONTROL_POINT_PATCHLIST = 64,
} D3D11_PRIMITIVE_TOPOLOGY;

所有的绘图操作以当前设置的图元拓扑方式为准。在没有改变拓扑方式之前，当前设置的拓扑方式会一直有效。下面的代码说明了一点：

md3dDevice->IASetPrimitiveTopology(
    D3D11_PRIMITIVE_TOPOLOGY_LINELIST); 
/* ...draw objects using line list... */ 
md3dDevice->IASetPrimitiveTopology(
    D3D11_PRIMITIVE_TOPOLOGY_TRIANGLELIST); 
/* ...draw objects using triangle list... */ 
md3dDevice->IASetPrimitiveTopology(
    D3D11_PRIMITIVE_TOPOLOGY_TRIANGLESTRIP); 
/* ...draw objects using triangle strip... */

下面的各小节会详细描述各种不同的图元拓扑方式。在本书中，我们主要使用三角形列表。

5.5.2.1 点列表

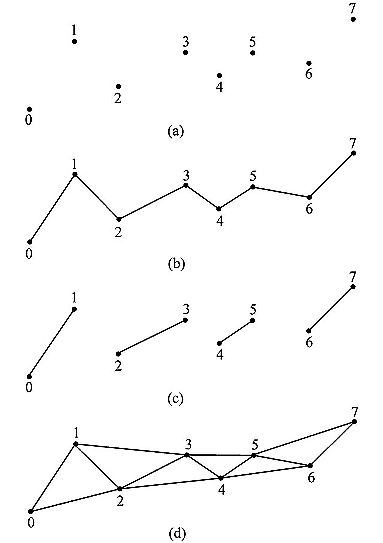
点列表（point list）由D3D11_PRIMITIVE_TOPOLOGY_POINTLIST标志值表示。当使用点列表时，每个顶点都会被绘制为一个独立的点，如图5.13a所示。

5.5.2.2 线带

线带（line strip）由D3D11_PRIMITIVE_TOPOLOGY_LINESTRIP标志值表示。当使用线带时，前后相邻的两个顶点会形成一条直线（参见图5.13b）；这样，n+1个顶点可以形成n条直线。

5.5.2.3 线列表

线列表（line list）由D3D11_PRIMITIVE_TOPOLOGY_LINELIST标志值表示。当使用线列表时，每两个顶点会形成一条独立的直线（参见图5.13c）；这样，2n个顶点可以形成n条直线。线列表和线带之间的区别是线列表中的直线可以断开，而线带中的直线会自动连在一起；因为内部的每个顶点由两条直线共享，所以线带使用的顶点数量更少。

5.5.2.4 三角形带

三角形带（triangle strip）由D3D11_PRIMITIVE_TOPOLOGY_TRIANGLESTRIP标志值表示。当使用三角形带时，顶点会按照图5.13d所示的带状方式形成连续的三角形。我们可以看到顶点由相邻的三角形共享，n个顶点可以形成n-2个三角形。

注意：偶数三角形和奇数三角形的顶点环绕顺序不同，由此会产生背面消隐问题（参见5.10.2节）。为了解决一问题，GPU会在内部交换偶数三角形的前两个顶点的顺序，以使它们的环绕顺序与奇数三角形相同。

5.5.2.5 三角形列表

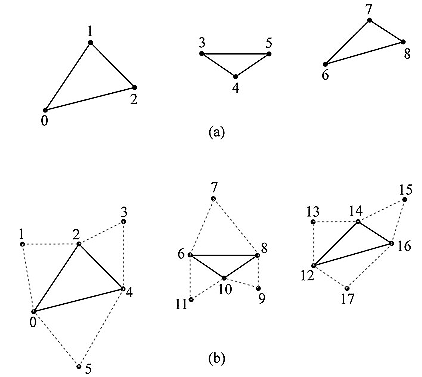
三角形列表（triangle list）由D3D11_PRIMITIVE_TOPOLOGY_TRIANGLELIST标志值表示。当使用三角形列表时，每三个顶点会形成一个独立的三角形（参见图5.14a）；这样，3n个顶点可以形成n个三角形。三角形列表与三角形带之间的区别是：三角形列表中的三角形可以断开，而三角形带中的三角形会自动连在一起。

5.5.2.6 带有邻接信息的图元

在包含邻接信息的三角形列表中，每个三角形都有与之相邻的3个邻接三角形；图5.14b说明了这些三角形的定义方式。它们主要用于几何着色器，因为某些几何着色算法需要访问邻接三角形。为了实现这些算法，邻接三角形必须与原三角形一起通过顶点/索引缓冲区提交给管线。通过指定D3D11_PRIMITIVE_TOPOLOGY_TRIANGLELIST_ADJ拓扑标志值可以使管线知道如何从顶点缓冲区中构建三角形以及它的邻接三角形。注意，邻接图元顶点只能作为几何着色器的输入数据——它们不会被绘制出来。如果没有几何着色器，那么邻接图元也不会被绘制出来。

线列表、线带和三角形带也可以包含邻接图元；详情请参见SDK文档。

5.5.2.7 控制点面片列表

D3D11_PRIMITIVE_TOPOLOGY_N_CONTROL_POINT_PATCHLIST拓扑标志表示将顶点数据作为N控制点的面片列表，这些点用于（可选）图形管线的曲面细分阶段（tessellation stage），我们要到第13章才会讨论到它。

5.5.3 索引

如前所述，三角形是构成3D物体的基本单位。下面的代码示范了使用三角形列表来构建四边形和八边形的顶点数组（即，每三个顶点构成一个三角形）。

Vertex quad[6] ={ 
    v0, v1, v2, // Triangle0 
    v0, v2, v3, // Triangle1 
}; 

Vertex octagon[24] ={ 
    v0, v1, v2, // Triangle0 
    v0, v2, v3, // Triangle1 
    v0, v3, v4, // Triangle2 
    v0, v4, v5, // Triangle3 
    v0, v5, v6, // Triangle4 
    v0, v6, v7, // Triangle5 
    v0, v7, v8, // Triangle6 
    v0, v8, v1    // Triangle 7 
};

注意：三角形的顶点顺序非常重要，我们将该顺序称为环绕顺序（winding order）；详情请参见5.10.2节。

如图5.15所示，构成3D物体的三角形会共享许多相同的顶点。更确切地说，在图5.15a中，四边形的每个三角形都会共享顶点v⁰和v²。当复制两个顶点时问题并不明显，但是在八边形的例子中问题就比较明显了（图5.15b），八边形的每个三角形都会复制中间的顶点v⁰，而且边缘上的每个顶点都由相邻的两个三角形共享。通常，复制顶点的数量会随着模型细节和复杂性的提高而骤然上升。

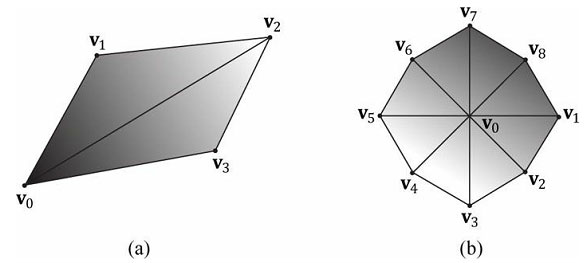
我们不希望对顶点进行复制，主要有两个原因：

1．增加内存需求量。（为什么要多次存储相同的顶点数据？）

2．增加图形硬件的处理负担。（为什么要多次处理相同的顶点数据？）

三角形带在一定程度上可以解决复制顶点问题，但是几何体必须按照带状方式组织，实现起来难度较大。相比之下，三角形列表具有更好的灵活性（三角形不必彼此相连），如果能找到一种方法，即移除复制顶点，又保留三角形列表的灵活性，那么会是一件非常有价值的事情。索引（index）可以解决一问题。它的工作原理是：我们创建一个顶点列表和一个索引列表。顶点列表包含所有唯一的顶点，而索引列表包含指向顶点列表的索引值，这些索引定义了顶点以何种方式组成三角形。回顾图5.15中的图形，四边形的顶点列表可以这样创建：

Vertex v[4] = {v0, v1, v2, v3};

而索引列表需要定义如何将顶点列表中的顶点放在一起，构成两个三角形。

UINT indexList[6] = {0, 1, 2,    // Triangle0 
    0, 2, 3}; // Triangle 1

在索引列表中，每3个元素表示一个三角形。所以上面的索引列表的含义为：“使用顶点v[0]、v[1]、v[2]构成三角形0，使用顶点v[0]、v[2]、v[3]构成三角形1”。

与之类似，八边形的顶点列表可以这样创建：

Vertex v[9] = {v0, v1, v2, v3, v4, v5, v6, v7, v8};

索引列表为：

UINT indexList[24] = { 
    0, 1, 2,    // Triangle 0 
    0, 2, 3,    // Triangle 1 
    0, 3, 4,    // Triangle 2 
    0, 4, 5,    // Triangle 3 
    0, 5, 6,    // Triangle 4 
    0, 6, 7,    // Triangle 5 
    0, 7, 8,    // Triangle 6 
    0, 8, 1    // Triangle7 
};

当顶点列表中的唯一顶点得到处理之后，显卡可以使用索引列表把顶点放在一起构成三角形。我们将“复制问题”转嫁给了索引列表，但是这种复制是可以让人接受的。因为：

1．索引是简单的整数，不像顶点结构体那样占用很多内存（顶点结构体包含的分量越多，占用的内存就越多）。

2．通过适当的顶点缓存排序，图形硬件不必重复处理顶点（在绝大多数的情况下）。

文件下载（已下载 1029 次）

发布时间：2014/7/27 下午8:30:39 阅读次数：8288