5.3 基本计算机颜色

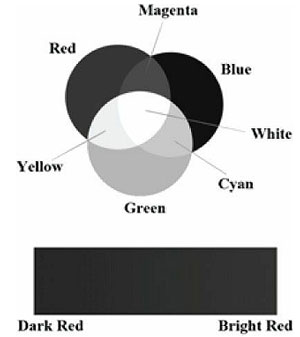
计算机显示器通过每个像素发射红、绿、蓝光的混合光线。当混合光线进入人的眼睛时会触碰到视网膜的某些区域，对锥感细胞产生刺激，神经触突会通过视觉神经传送到大脑。大脑会解释些信号并生成颜色。随着混合光线的变化，细胞会受到不同的刺激，从而在我们的思想意识中产生不同的颜色。图5.8说明了红、绿、蓝三色的混合方式以及不同强度的红色。通过为每个颜色分量指定不同的强度并对其进行混合，可以描述我们所要显示的真实图像中的所有颜色。

读者可以使用绘图软件（比如Adobe Photoshop）或Win32颜色对话框（图5.9）进一步了解如何使用RGB（red、green、blue）值来描述颜色。尝试使用不同的RGB组合，看一看它们产生的颜色。

显示器所能发射的红、绿、蓝光的强度有最大限制。我们使用从0到1的规范化区间来描述光线强度。0表示没有强度，1表示最高强度。中间值表示中等强度。例如，值（0.25,0.67,1.0）表示混合光由强度为25%的红光、强度为67%的绿和强度为100%的蓝光组成。如本例所示，我们可以通过3D向量（r,g,b）来表示颜色，其中0≤r，g，b≤1，三个颜色分量分别描述红、绿、蓝光的强度。

5.3.1 颜色运算

某些向量运算也适用于颜色向量。例如，我们可以把颜色向量加在一起得到一个新的颜色：

(0.0, 0.5, 0.0) + (0.0, 0.0, 0.25) = (0.0, 0.5, 0.25)

通过混合一个中等强度的绿色和一个低强度的蓝色，得到一个深绿色。也可以通过颜色相减来得到一个新的颜色：

(1, 1,1) − (1, 1,0) = (0, 0,1)

也就是，我们从白色中减去它的红色和绿色部分，得到最终的蓝色。

标量乘法也有意义。例如：

0.5(1, 1,1) = (0.5, 0.5, 0.5)

也就是，将白色乘以0.5，得到一个中等强度的灰色。而运算2(0.25, 0.0, 0.0) = (0.5, 0.0, 0.0)，可使红色分量的强度增大一倍。

颜色向量的点积和叉积没有意义。不过，颜色向量有一种特殊的乘法运算，叫做分量乘法（componentwise multiplication）。其定义如下：

(c_r,c_g,c_b)⨂(k_r,kg,k_b) = (c_rk_r,c_gk_g,c_bk_b)

这一运算主要用于光照方程。例如，一个颜色为(r,g,b)的入射光，照射在一个平面上。该平面反射50%的红光、75%的绿和25%的蓝光，其余线均被平面吸收。则折回的反射光颜色为：

(r,g,b)⨂(0.5,0.75,0.25) = (0.5r,0.75g,0.25b)

我们可以看到，由于平面吸收了一些线，所以当光线照射在平面上时会丢失一些颜色。

当进行颜色运算时，某些颜色分量可能会超出[0,1]区间；例如，方程(1,0.1,0.6) + (0.0,0.3,0.5) = (1,0.4,1.1)。由于1.0表示颜色分量的最大强度，任何分量都不能大于该值。所以，我们要把1.1截取为1.0。同样，显示器不能发射负光，所以任何负的颜色分量（负值是由减法运算取得的结果）都必须截取为0.0。

5.3.2 128位颜色

通常，在颜色中会包含一个附加的颜色分量，叫做alpha分量。alpha分量用于表示颜色的不透明度，我们会在第9章“混合”中使用alpha分量。（由于我们目前还用不到混合，所以现在暂且将alpha分量设置为1。）

包含alpha分量意味着我们要使用4D向量(r,g,b,a)来表示颜色，其中0≤r,g,b,a≤1。要表示一个128位颜色，可以为每个分量指定一个浮点值。因为从数学上来说，颜色就是一个4D向量，所以我们可以在代码中使用XMVECTOR类型表示一个颜色，而且还可以利用XNA数学矢量函数所用的SIMD操作带来的优势进行颜色运算（例如颜色相加、相减、标量乘法）。对于分量乘法，XNA数学库提供了以下方法：

XMVECTOR XMColorModulate(// Returns (cr, cg, cb, ca) ⊗ (kr,kg,kb,ka)
    FXMVECTOR C1, // (cr, cg, cb, ca)
    FXMVECTOR C2 // (kr, kg, kb, ka) 
);

5.3.3 32位颜色

当使用32位表示一个颜色时，每个字节会对应于一个颜色分量。由于每个颜色分量占用一个8位字节，所以每个颜色分量可以表示256种不同的明暗强度——0表示没有强度，255表示最高强度，中间值表示中等强度。从表面上看，为每个颜色分量分配一个字节似乎很小，但是通过计算组合值（256×256×256 = 16,777,216）可以发现，这种方式可以表示上千万种不同的颜色。XNA数学库提供了以下结构用于存储32位颜色：

// ARGB Color; 8-8-8-8 bit unsigned normalized integer components packed into
// a 32 bit integer.  The normalized color is packed into 32 bits using 8 bit
// unsigned, normalized integers for the alpha, red, green, and blue components.
// The alpha component is stored in the most significant bits and the blue
// component in the least significant bits (A8R8G8B8):
// [32] aaaaaaaa rrrrrrrr gggggggg bbbbbbbb [0]
typedef struct _XMCOLOR
{
    union
    {
        struct
        {
            UINT b    : 8;  // Blue:    0/255 to 255/255
            UINT g    : 8;  // Green:   0/255 to 255/255
            UINT r    : 8;  // Red:     0/255 to 255/255
            UINT a    : 8;  // Alpha:   0/255 to 255/255
        };
        UINT c;
    };

#ifdef __cplusplus

    _XMCOLOR() {};
    _XMCOLOR(UINT Color) : c(Color) {};
    _XMCOLOR(FLOAT _r, FLOAT _g, FLOAT _b, FLOAT _a);
    _XMCOLOR(CONST FLOAT *pArray);

    operator UINT () { return c; }

    _XMCOLOR& operator= (CONST _XMCOLOR& Color);
    _XMCOLOR& operator= (CONST UINT Color);

#endif // __cplusplus

} XMCOLOR;

通过将整数区间[0,255]映射到实数区间[0,1]，可以将一个32位颜色转换为一个128位颜色。这一映射工作是通过将每个分量除以255来实现。也就是，当n为0到255之间的一个整数时，对应于规范化区间[0,1]的分量值为0≤\(\frac{n}{{255}}\)≤1。例如，32位颜色(80,140,200,255)变为：

(80,140,200,255) → (\(\frac{{80}}{{255}},\frac{{140}}{{255}},\frac{{200}}{{255}},\frac{{255}}{{255}}\) ) ≈ (0.31,0.55,0.78,1.0)

另一方面，通过将每个颜色分量乘以255并进行四舍五入，可以将一个128位颜色转换为一个32位颜色。例如：

(0.3,0.6,0.9,1.0) → (0.3*255,0.6*255,0.9*255,1.0*255) = (77,153,230,255)

当把一个32位颜色转换为一个128位颜色或者进行反向转换时，通常要执行额外的位运算，因为8位颜色分量通常会被封装在一个32位整数中（例如，无符号整数），即在XMCOLOR中。XNA数学库使用以下函数处理一个XMCOLOR并以XMVECTOR的形式返回：

XMVECTOR XMLoadColor(CONST XMCOLOR* pSource); 

图5.10说明了如何将4个8位颜色分量封装为一个无符号整数。注意，这只是用于封装颜色分量的方式之一。除使用ARGB外，还可以使用ABGR或RGBA。不过，XMCOLOR类使用ARGB格式。XNA数学库提供了一个函数可以将一XMVECTOR颜色转化为一个XMCOLOR：

VOID XMStoreColor(XMCOLOR* pDestination,FXMVECTOR V);

通常，许多颜色运算（例如，在像素着色器中）使用的都是128位颜色值；通过这一方式，我们可以有足够多的二进制位来保证计算的精确度，减少算术错误的累积。不过，最终的像素颜色通常是存储在后台缓冲区的32位颜色值中；目前的物理显示设备还不能充分利用更高的分辨率颜色。

发布时间：2014/7/27 下午8:03:37  阅读次数：5351