地面上测量物体质量的装置设计（二）

高二（2）班 高铭鸿 孙萌 施展

1．装置示意图

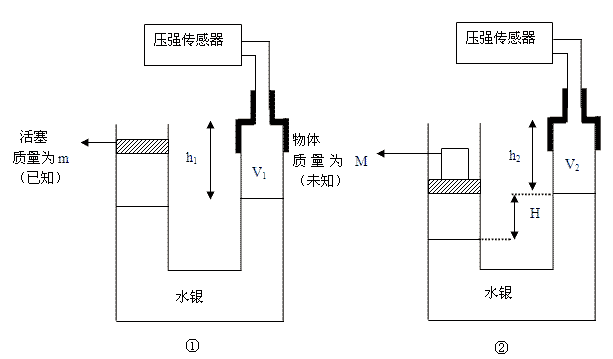
2．实验器材

两端开口的U型管、橡皮管、一定体积水银、已知质量m的活塞、压强传感器、刻度尺。

3．实验原理

用压强传感器测量出气体压强p₁，根据U型管横截面积和测量出液面与管顶端的液面差h₁，计算出V₁。把质量为M（未知）的待测物体放到活塞上，用刻度尺测量测量液面与管顶端的液面差h₂，计算出V₂。已知p₁、V₁、V₂，根据波意耳定律p₁V₁＝p₂V₂，求出右边气体的压强p₂＝\(\frac{{{p_1}{h_1}S}}{{{h_2}S}}\)＝p_右。对用刻度尺测量出左右水银柱的高度差H，满足方程p_左＝p_右＋ρgH，求得左边气体的p_左。对左边的活塞m和物体M做受力分析，物体要保持平衡，满足方程（M＋m）g＋p₀S＝p_左S，最终得出M。

4．实验步骤

（1）测量U型管内壁横截面积，记为S，用压强传感器测量外界大气压压强p₀；

（2）在U型管中加入一定量的水银，在右端用橡皮管与压强传感器相连（密封），向左端放入质量为m的活塞（能自由活动），并记录压强传感器的数值记为p₁和用刻度尺测量液面与管顶端的液面差h₁，根据V₁＝h₁S，求出V₁；

（3）把质量为M（未知）的待测物体放到活塞上，用刻度尺测量测量液面与管顶端的液面差h₂，计算出V₂＝h₂S；

（4）根据波意耳定律p₁V₁＝p₂V₂计算出右边气体的压强p₂＝\(\frac{{{p_1}{h_1}S}}{{{h_2}S}}\)＝p_右。

（5）用刻度尺测量出左右水银柱的高度差H，满足方程p_左＝p_右＋ρgH，求得左边气体的压强：p_左＝p_右＋ρgH＝\(\frac{{{p_1}{h_1}}}{{{h_2}}}\) ＋ρgH。

（6）对左边的活塞m和物体M做受力分析，物体要保持平衡，满足方程（M＋m）g＋p₀S＝p_左S，最终得出\(M = \frac{{S({p_1}{h_1} + \rho gH{h_2}) - {p_0}S{h_2}}}{{g{h_2}}} - m\)。

5．实验误差

（1）与压强传感器相连接的橡皮管内的气体也有体积，会产生实验误差，因此尽可能使用体积可以忽略不计的橡皮管，或者测量的时候应把这部分气体的体积也加入进去。

（2）活塞两壁有摩擦力，活塞和物体压力可能有误差，需事先润滑。

高二（2）班 王悦 蔡浩天

1．装置示意图

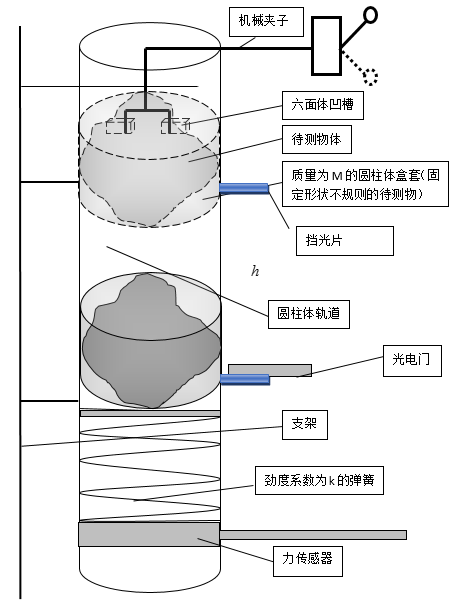
2．实验器材

圆柱体轨道（有一条边带有缺口），圆柱体盒套（质量为M），挡光片，支架，力传感器，光电门，弹簧（上端带有轻质挡板），机械夹子。

3．实验原理

将待测物体（质量为m）放入盒套内，用机械夹子夹住圆柱体盒套（盒套的内径比轨道略小），机械夹子松开盒套，将盒套连同待测物体从静止释放，做自由落体运动。测量出盒套低端与光电门的距离h，并测出盒套低端通过光电门的速度，则物体所在处的重力加速度为g＝\(\frac{{v_2^2}}{{2h}}\)；利用力传感器测得弹簧对传感器这段时间内的最大压力F，便可以求出弹簧的最大形变量x＝\(\frac{{{F_{\max }}}}{k}\)；利用能量守恒定律，物体的重力势能等于弹簧的弹性势能，E_p＝E_k即可求出物体质量：

（M＋m）g（h＋x）＝\(\frac{1}{2}\)kx²

\(m = \frac{{hF_{\max }^2}}{{{v^2}k(h + x)}} - M\)

备注：光电门与弹簧顶端在同一平面上。

4．实验步骤

（1）将待测物放入圆形盒套中并固定在机械夹子上。

（2）测出盒套底端与光电门的距离h；

（3）将开关向上推，机械夹子松开圆形盒套，盒套与物体从静止开始做自由落体运动，经过光电门测得末速度v。

（4）当盒套碰到轻质挡板，压缩弹簧后，力传感器测得弹簧对传感器这段时间内的最大压力F，求出弹簧的最大形变量x＝\(\frac{{{F_{\max }}}}{k}\)。

（5）利用能量守恒定律，物体的重力势能等于弹簧的弹性势能，E_p＝E_k即可求出物体质量：

\(m = \frac{{hF_{\max }^2}}{{{v^2}k(h + x)}} - M\)

5．实验误差

（1）释放圆形盒套后，若盒套与管道接触，可能产生摩擦力，应事先对管道进行润滑，以减小摩擦力。

（2）弹簧上的挡板存在质量，会对实验产生误差，因尽可能选取轻质的挡板。

高二（4）班 房欣琰 颜欣薏 李杰

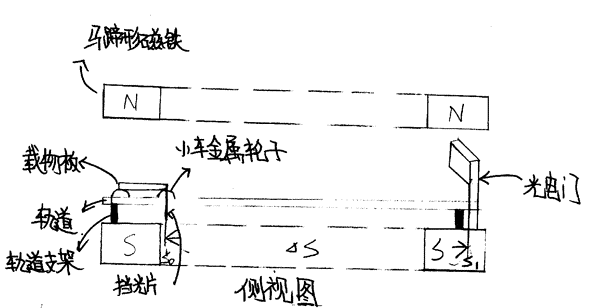
1．装置示意图

斜视图：

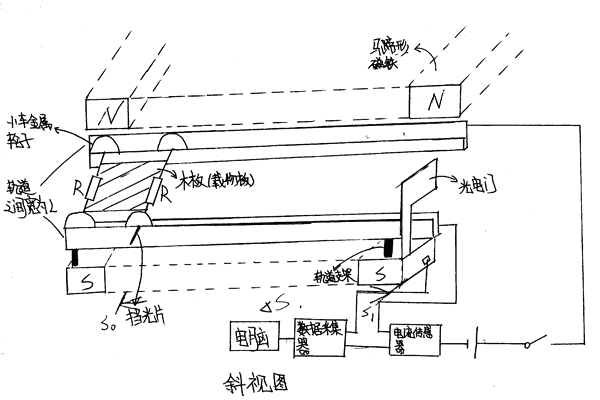
正视图：

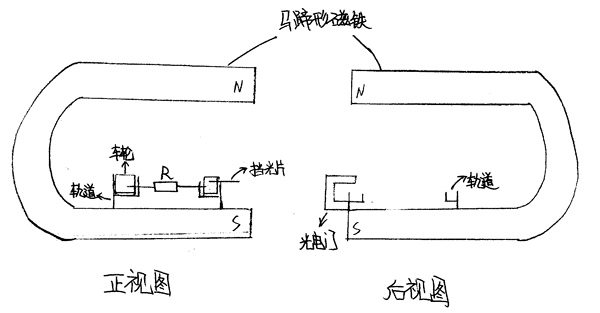
侧视图：

2．实验器材

多组马蹄形磁铁、刻度尺、绝缘棒（轨道支架）、带有刻度尺的金属卡槽轨道、两个带有相同电阻的金属车轴、4个小车金属轮子、木板（载物板）、导线、电源、电键、挡光片、磁传感器、光电门、电流传感器、数据采集器、电脑。

3．实验原理

利用磁传感器测出马蹄形磁铁的磁感应强度B（前段近似看成匀强磁场），利用电流传感器测出通过金属车轴的电流I，利用光电门测出挡光片通过光电门的速度v，利用卡槽轨道上的刻度尺测出小车静止时挡光片与光电门挡光处的距离S，利用刻度尺测出轨道的宽度L。由于小车在匀强磁场中受到安培力的作用，从静止开始做匀加速直线运动，因此只要测出上述物理量，通过物理公式：

BIL＝ma

BIL＝m\(\frac{{v_2^2}}{{2S}}\)

\(m = \frac{{2SBIL}}{{{v^2}}}\)

就可以测出物体的质量。

4．实验步骤

（1）用磁感应器测出马蹄形磁铁的磁感应强度B（前段近似看为匀强磁场）；

（2）测出轨道的宽度为L；

（3）将小车放在轨道上，记下挡光片所在的初始位置与光电门挡光处的距离为S1；

（4）接通电键，小车在安培力的作用下从静止开始做匀加速直线运动。记录下挡光片通过光电门时的v₁；

（5）记录下电流传感器示数为I，由于两个车轴的电阻相等，F＝\(\frac{{BIL}}{2}\) ＋\(\frac{{BIL}}{2}\)＝BIL，所以：

BIL＝M_车\(\frac{{v_2^2}}{{2S}}\)

M_车＝\(\frac{{2BIL{S_1}}}{{v_1^2}}\)

（6）放上待测物体后，重新进行上述实验，并测出S₂和v₂（BIL数值大小不变）

M_车＋m_物＝\(\frac{{2BIL{S_2}}}{{v_2^2}}\)

所以：m_物＝\(\frac{{2BIL{S_2}}}{{v_2^2}}\)－M_车

5．实验误差

（1）由于轨道与小车存在摩擦力，会对实验的测量结果造成误差，因此可在轨道上涂上润滑剂，减小小车所受到的摩擦力。

（2）由于金属轨道上也有电阻，会对实验的测量结果造成误差，因此尽可能选取电阻率较小的金属制成金属轨道。

高二（8）班 秦嘉杰 沈荻伟 周叙辰

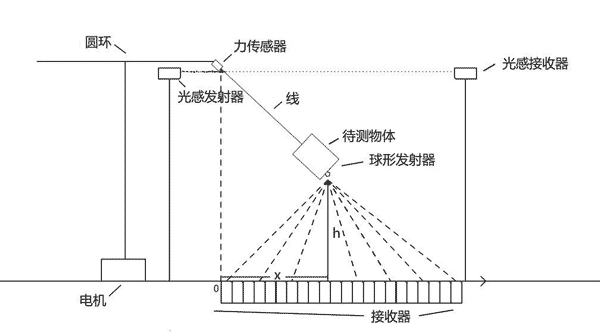
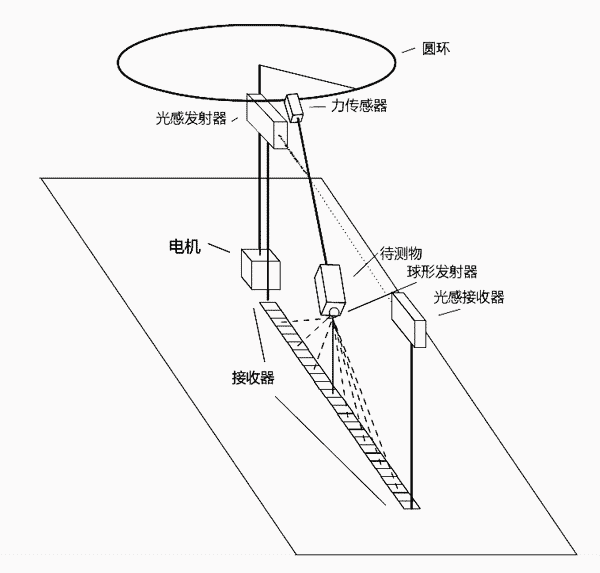
1．装置示意图

平面图：

立体图：

2．实验器材

电动机，圆环型支架（高H），长方形载物容器（已知质量为M₁），细绳，刻度尺，力传感器，球型信号发射器（已知质量为M₂），信号接收器一排，激光发射器，激光接收器，数据采集器，计算机。

3．实验原理

当开始实验时，用电动机带动圆环型支架速转动，当绳子不挡光时，激光发射器和激光接收器在不断工作，放置待测物体的长方形载物容器上的球型信号发射器和力传感器工作，地面上接受球型信号发射器的信号接收器不工作。

当绳子挡住激光发射器的激光时，地上的信号接收器开始工作。

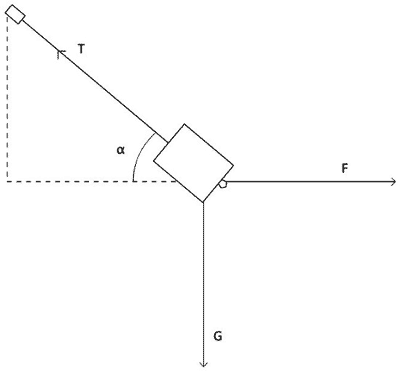
以力传感器正下方的信号接收器为x轴的原点，球型信号发射器向四面八方发射信号，地上所排列的每个接收器都会接收到发散型信号发射器的信号，从而测量出物体与地面所放置的各个信号传感器的距离，并经分析选取数值最小的数据（即物体与地面的垂直距离h)，并找出最小h对应的x坐标。同时力传感器记录此时的拉力T。将绳子与长方形载物容器的长用刻度尺测出为L，那么对物体的受力分析并根据公式，得到物体质量。

Tsinα＝mg

T\(\frac{{\sqrt {{L^2} - {x^2}} }}{L}\)=mg

\(m = \frac{{T\sqrt {{L^2} - {x^2}} }}{{gL}}\)

4．实验步骤

（1）用刻度尺测出绳子和长方形载物容器的总长度L。

（2）在圆环上套上一根绳子，将力传感器固定在绳子靠近顶端位置，细绳末端固定长方形载物容器。

（3）将球型信号发射器固定在长方形载物容器末端（长方形载物容器质量为M₁，球型信号发射器质量为M₂），将待测物体（质量为m未知）装入容器中，绳子自然下垂。

（4）将所有传感器连接数据采集器并与电脑相连，运行设定程序。

（5）用电动机带动圆环型支架匀速转动，开始实验。

（6） 当细绳挡住激光发射器和激光接收器的信号传输时，地面上的信号接收器开始工作，接受到球型信号发射器，得出物体与地面的最短距离即垂直距离h，同时得出垂直距离h所对应的x坐标。

（7）力传感器同时记录下绳子上的拉力T。

（8）根据Tsinα＝（M₁＋M₂＋m）g

所以

\(m = \frac{{T\sqrt {{L^2} - {x^2}} }}{{gL}}\) －M₁－M₂

5．实验误差

（1）在力传感器和圆环间用一个可以自由活动的圆扣连接，使力传感器和绳子在同一直线上，避免产生夹角导致力的误差。

（2）力传感器末端与地面上信号接收器对齐，避免x产生误差。

（3）重复实验，得出平均值，减少误差。

高二（8）班 倪凯熠 虞震泽 周楷祺

1． 装置示意图

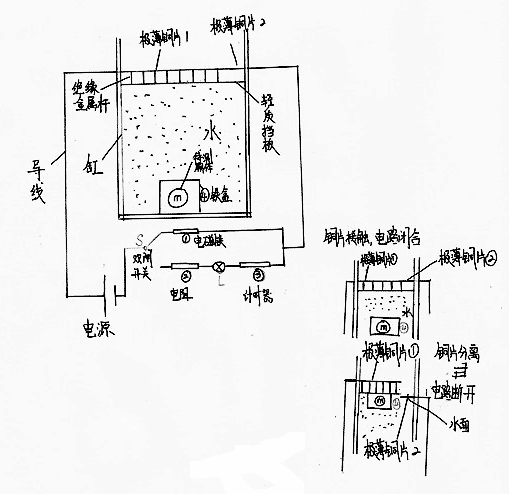
2． 实验器材

透明水箱，一个密封且中空可容纳物体的铁盒（已知质量M，已知体积V），轻质挡板一块，极薄铜片两块，导线，电阻一个，电磁铁一块，指示小灯一只，计时器一个，开关一个，绝缘金属杆若干。

3．实验原理

根据阿基米德定律，可由公式得出F_浮＝ρgV且由于排液的量始终不变，故浮力为恒力。

铁盒由于受到合外力恒力为：

F_合＝F_浮－G_总

F_浮－（M＋m）g＝（M＋m）a

在此力作用下，铁盒由缸底从静止作匀加速直线运动。

测出铁盒上表面到轻质挡板的距离，以及读出计时器的示数，根据a＝\(\frac{{2S}}{{{t^2}}}\)，可得出加速度a的大小。根据牛顿第二定律，可知F_合＝（M＋m）a

将已知物理量代入，得出

m＝\(\frac{{\rho gV{t^2}}}{{{t^2} + 2S}}\)－M

式中M为铁盒质量，V为铁盒的体积。

4．实验步骤

（1）首先按照示意图安装器材；

（2）将需要测量的物体（质量为m）放入铁盒内，并放入透明水箱内；

（3）接通电源，将带有电磁铁的支路接通，电磁铁吸引铁盒且将铁盒固定在透明水箱底；

（4）向透明水箱内注入水至水溢出；

（5）将轻质挡板推至与水面相平处；

（6）测量铁盒顶端至轻质挡板距离，记作S；

（7）将开关与带有计时器的支路接通，电磁铁磁力消失，铁盒上浮，计时器开始计时，指示灯亮起；

（8）铁盒上浮，由于全程完全浸没于水中，故F为恒力不变，F_浮＝ρgV；

（9）铁盒撞击轻质挡板，极薄铜片1被弹起，电路断开，计时器停止工作，得到时间t；

（10）由于铁盒做匀加速直线运动，可得a＝\(\frac{{2S}}{{{t^2}}}\)；

（11）由F_浮－（M＋m）g＝（M＋m）a可得：

m＝\(\frac{{\rho gV{t^2}}}{{{t^2} + 2S}}\)－M

5．实验误差

（1）可能由于挡板质量过重，铁盒撞击时电路未能断开，从而导致误差的产生。为此，需要将挡板以及绝缘金属杆的质量降至最低。

（2）可能由于开关断开电磁铁时未能及时接通计时器，从而导致误差的产生。可以通过减小开关的间距，减小时间差。

发布时间：2014/1/5 下午9:15:33  阅读次数：4734