地面上测量物体质量的装置设计（一）

高二（1）班 许忆枫 王竑冰 郦煜 薛凯文 王忠 朱华江 林平

1．实验原理

物体做圆周运动时受到向心力的大小应满足F_向＝\(m\frac{{{v^2}}}{r}\)，若我们能测出物体m做圆周运动时受到的向心力F_向、线速度v及运动半径r，则可以通过下列公式求出待测物体的质量m：

\(m = \frac{{{F_向}r}}{{{v^2}}}\) （1）

为了让实验操作更加简单，我们可以使用一根细绳系住待测物体，使之在竖直平面做圆周运动，在这种情况中，公式（1）可以写成：

\(m = \frac{{(T - mg)l}}{{{v^2}}}\) （2）

经过整理可以得出m的表达式：

\(m = \frac{T}{{g + \frac{{{v^2}}}{l}}}\) （3）

公式（3）中的T为待测物体在最低点时细绳的拉力大小，它可以通过力传感器测出；g为当地重力加速度，v为待测物体通过最低点时的速度大小，它可以通过光电传感器测出；l为细绳长度，由刻度尺量出。

2．装置示意图

如图1所示：

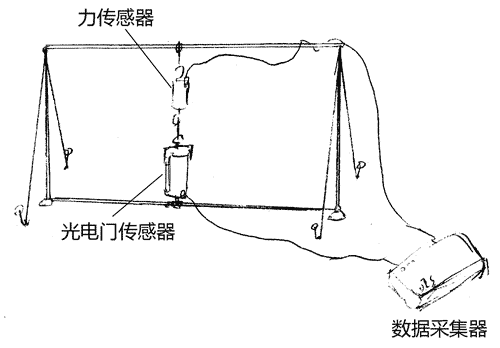
3．实验器材

细绳、门字形支架、力传感器、光电门传感器、数据采集器、计算机、挡光片。

4．操作步骤

（1）将挡光片（宽度约2mm左右）连接在待测物体下方，将待测物体连接在细绳上。挡光片的放置方式如图2所示：

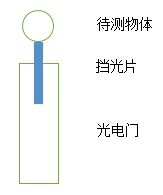
（2）将力传感器和光电门传感器分别接入数据采集器的端口1、2，对应的变量分别为F1、t2，然后添加挡光片宽度d，初始值设置为0.002m；添加速度变量v，设置公式为v＝d/t2；设置绳长变量l，由刻度尺量出，这里设置为1m，最后设置变量m，设置公式为m＝F1/(9.8+v^2/l)。数据表格窗口如下图3所示：

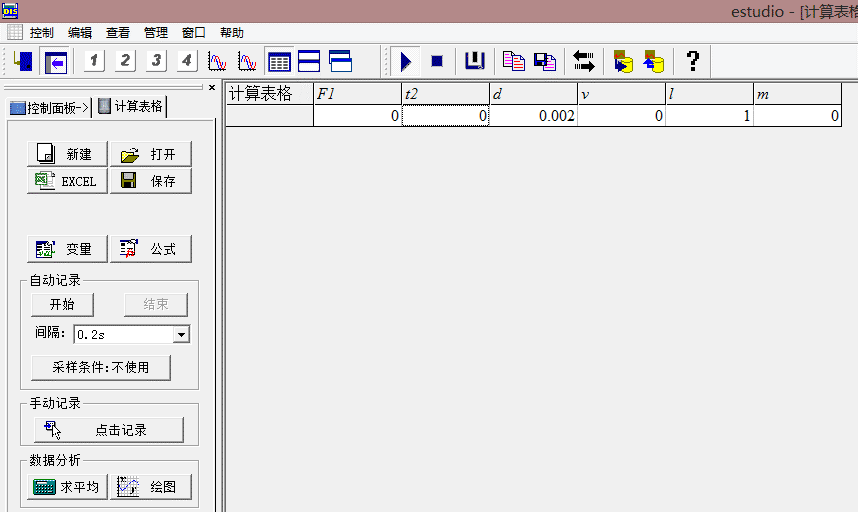
（3）打开数据采集器，进行调零，测试力传感器以及光电门是否正常工作。

（4）将待测物体拉开一定角度后由静止释放，使挡光片可以遮挡住光电门的探测孔，如若不能，则需调节光电门的上下位置；

（5）调整正常后，将待测物体拉开一定角度后由静止释放，在数据表格中的m列中就会显示出待测物体的质量。

高二（1）班 李紫莹 王诚琪 潘宸 张怡耘

1．实验原理

若在一个光滑的水平桌面上，放一个质量为m的物体，用一个水平弹簧与其相连，弹簧的另一端固定。物体可静止于使弹簧保持其自然长度的位置，称为平衡位置。当弹簧被拉离平衡位置之后，形变将使其产生一个水平弹性回复力，其方向指向平衡位置。这里重力与桌面的支撑力相抵消，不影响其水平运动。在弹性回复力的作用下，物体会围绕平衡位置振动，其振动周期为\(T = 2\pi \sqrt {\frac{m}{k}} \)，这里的k为弹簧的劲度系数。若测量出弹簧劲度系数及振动频率，则可以从上式中解出质量m的值。

可以证明，当将弹簧竖直挂上一个质量为m的物体时，弹簧将被拉长，并可静止于一个平衡位置。当弹费被拉离这个平衡位置并释放时，它将围绕平衡位置上下振动，其振动周期与水平振子的公式相同。在微重力条件下，振子振动周期的计算公式仍然不变。因此，我们可以从振动周期和劲度系数计算得到物体的质量。

为了让测量更加简单并减小误差，我们采用了双弹簧振子的装置，并在此原理的基础上又做了一些改进：

首先测出一个已知质量M物体做N次全振动的时间t₁，此时应满足：

\(\frac{{{t_1}}}{N} = 2\pi \sqrt {\frac{M}{k}} \)（1）

然后将待测物体m与已知质量M的物体合并在一起，仍测出它们做N次全振动的时间t₂，此时应满足：

\(\frac{{{t_2}}}{N} = 2\pi \sqrt {\frac{{M + m}}{k}} \)（2）

联立（1）（2）两式得：

\(\frac{{t_1^2}}{{t_2^2}} = \frac{M}{{M + m}}\) （3）

即：\(m = \frac{{t_2^2 - t_1^2}}{{t_1^2}}M\) （4）

由公式（4）可知，我们只需测出t₁、t₂，代入上述数据即可求出待测物体的质量m。而且，当实验装置确定之后，t₁只需测一次，以后都可以作为已知量处理，因此在测量时只需测定一个物理量t₂即可。

2．装置示意图

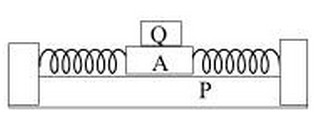
3．实验器材

光滑导轨、两根的弹簧（k并不需要测出，k不同亦可），质量M已知的物块A、秒表。

4．操作步骤

（1）不放待测物体Q，使A偏离平衡位置做简谐振动，用秒表测出弹簧振子振动N所需的时间t₁。

（2）将待测物体Q固定在物块A上，仍使A偏离平衡位置做简谐振动，用秒表测出弹簧振子振动N所需的时间t2。

（3）将测得的物理量代入公式\(m = \frac{{t_2^2 - t_1^2}}{{t_1^2}}M\) ，即可求出待测物体的质量m。

说明：比起王亚平老师介绍的弹簧振子，使用这种装置无需知道弹簧的劲度系数。而且这种装置可以在太空中正常使用，我们可以在地面上测出物体Q的质量M、周期T₁＝t₁/N ，上述两个物理量在太空中不会发生变化，为了舒适起见、可以将Q做成椅子。在太空中时，质量未知的航天员坐在椅子上，使之做简谐振动，可以使用光电门传感器代替秒表测量振动周期T₂，这样使用如下公式：

\(m = \frac{{T_2^2 - T_1^2}}{{T_1^2}}M\)

就可以非常快地测量出航天员的质量，此装置结构简单，具有很高的实用价值。

高二（3）班 赵余晨 韩梦珺 吴闻硕 邱逸平

1．实验原理

我们从DIS通用实验——“向心力的研究”中汲取了灵感，此实验的目的是研究向心力与质量、半径和角速度的关系，但在步骤中稍作调整，就可以成为一个测量物体质量的装置。

做圆周运动的物体所受向心力应满足F_向＝mω²r，此公式可变形为：

\(m = \frac{{{F_向}}}{{{\omega ^2}r}}\) （1）

也就是说，只需测出向心力、角速度、圆半径，即可代入公式（1）求出待测物体的质量。为了提高结果的准确度且便于处理，我们可以多次测量F_向和ω，然后在F_向-ω²图像中进行描点，并进行直线拟合，求出此直线的斜率k。最后待测物体的质量m可以下列公式求得：

\(m = \frac{k}{r}\) （2）

2．装置示意图

如图1所示：

3．实验器材

DIS向心力实验器及配件。

4．操作步骤

（1）将光电门传感器和力传感器分别接入数据采集器；

（2）按实验装置图把两个传感器固定在向心力实验器上，实验器有关参数：挡光杆直径0.005m、挡光杆到轴心的距离0.14m；

（3）将实验器调节为水平，对力传感器调零，把待测砝码固定在离轴心0.12m处；

（4）打开“计算表格”窗口，点击“开始”，转动实验器的悬臂，记录F、t数据；

（5）点击“公式”，输入计算线速度和角速度的公式：v=0.005/t1、ω=v/0.14、q=w^2，得到计算结果；如下图2所示：

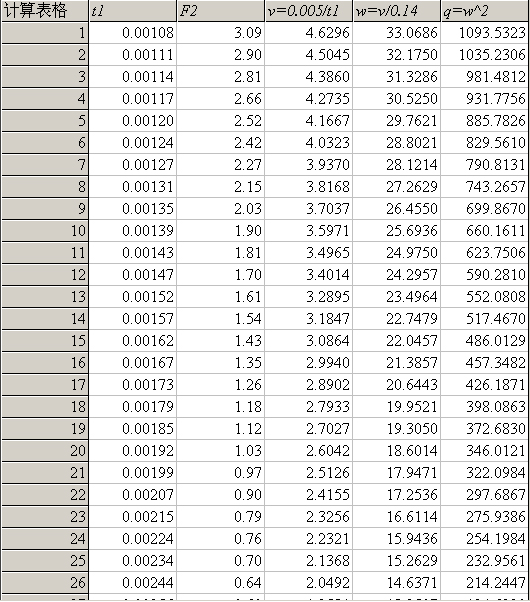
（6）点击“绘图”，选取X轴为“q”，Y轴为“F2”，得到数据点在坐标系内的分布图，点击“线性拟合”，拟合图线为过原点的直线。如下图3所示：

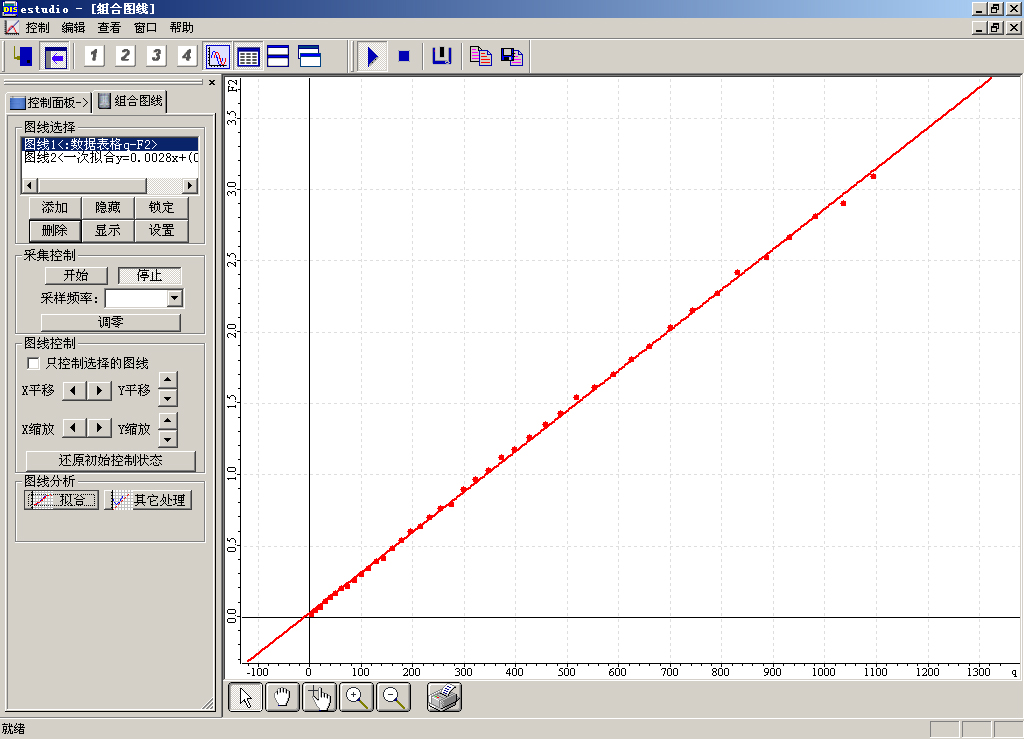
（7）在左侧的图线选择框中可以看到拟合方程：

y＝0.0028x

由向心力公式F＝mω²r可知，F-ω²图线的斜率对应的物理量为mr，即mr＝0.0028，而r＝0.12m是已知的，因此待测砝码的质量为m＝0.023kg。

说明：这个装置在太空中仍然可以正常使用，且携带方便、测量精度高。

高二（7）班 戴中钦 程彦煜 董振宇 吴逸飞 顾成杰 黎之豪 徐瀛

1．实验原理

万有引力定律告诉我们，任何两个有质量的物体之间存在相互吸引力，这个力叫做万有引力定律，它的大小可以由以下公式得到：

\(F = G\frac{{mm'}}{{{r^2}}}\) （1）

式中G为万有引力恒量，其大小为6.67×10^-11N•m²/kg²。因此，只需测出F、r、m，就可以通过公式（1）的变形：

\(m' = \frac{{F{r^2}}}{{mG}}\) （2）

得到待测物体的质量mʹ。然而，由于万有引力恒量很小，因此F通常很小，用常规测力的方法误差偏大。我们借鉴了卡文迪许扭秤装置，用两种方法解决了测量微小力的难点：

• 将测力转变为测石英丝的扭矩；
• 利用了光尺放大技术。

当一束光照射到固定在游丝上的反射镜上时，若光线与圆镜的法线有一微小角度时，反射光则以与入射角相同的角度反射到远处的光尺上，一般光尺到圆镜的距离有几十厘米，所以反射光的光点在光尺上就划过一个较大距离，这样游丝的微小转动在光尺上就能读到一段较大的尺寸，使微小量得到了放大。由以上说明，此装置在平衡时应该满足的方程是：

\(k\theta = G\frac{{mm'}}{{{r^2}}} \cdot \frac{l}{2}\) （3）

可得：

\(m' = \frac{{2k\theta {r^2}}}{{Gml}}\)（4）

公式（4）中k为石英丝的扭转系数，r为m与mʹ间的距离，θ为支架偏转角度，m为小球的质量，l为支架水平横梁的长度。在实际应用中，k、m、l都是已知量，因此只需测量r和θ即可。

2．实验装置

图1为装置的立体图。

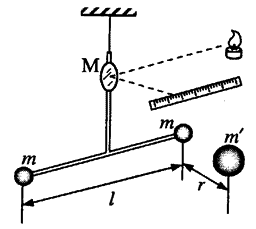
为了使测量θ的过程更简单，我们可以将直刻度尺做成圆弧状，并将表示长度的刻度替换成角度，这样无需进行转换就可以直接读出支架偏转的角度θ，如图2所示：

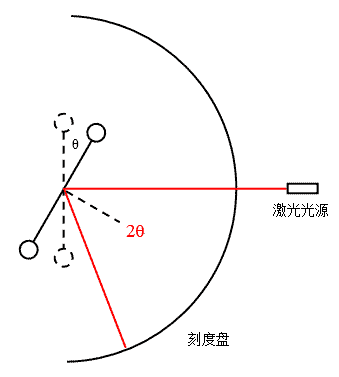
3．实验器材

轻质T形支架，两个质量m已知的小球，扭转系数k已知的石英丝，激光光源，刻度尺，平面反光镜。

4．实验步骤

（1）将轻质T形架倒挂在石英丝的下端，T形架水平部分的两端，各装一个质量是m的小球，T形架的竖直部分装一面小平面镜M，能把射来的光线反射到一根刻度尺上。

（2）把待测物mʹ放在m附近，由于m受到mʹ的吸引，使T形支架受到扭转力矩而转动，同时石英丝发生扭转，产生相反的扭转力矩，阻碍T形架转动，当这两个扭转力矩产生的效果相抵消时，T形架停下来不动。

（3）此时从弧形刻度尺上读出石英丝扭转的角度θ，用刻度尺量出m与mʹ的距离r。

（4）代入公式\(m' = \frac{{2k\theta {r^2}}}{{Gml}}\)求出待测物mʹ的质量。

5．说明

这个测量质量的装置在太空中仍可以使用。但由于装置无法做得太大，因此量程不大，无法测量质量太大的物体。

高二（7）班 龚思斌 张金杰明 周嘉懿 王之豪 汪世洋 周嘉辰 韩子昆 赵嘉宸

1．实验原理

动量守恒定律告诉我们，若两个质量为m₁，m₂的物体发生完全非弹性碰撞，应满足下列公式：

m₁v₁＋m₂v₂＝（m₁＋m₂）v （1）

公式（1）中的v₁、v₂、v分别是物体m₁的初速、m₂的初速、碰撞后m₁和m₂的共同速度，若已知m₂、v₁、v₂、v，就可以通过公式（1）的变形求出m₁的质量：

\({m_1} = \frac{{{m_2}(v - {v_2})}}{{{v_1} - v}}\) （2）

为了减小测量误差，我们可以使v₂＝0，且用如下图1所示的装置测量碰撞后两者上升的高度，这样就可以通过机械能守恒定律间接地求得\(v = \sqrt {2gh} \)，这样公式（2）就可以简化为：

\({m_1} = \frac{{{m_2}\sqrt {2gh} }}{{{v_1} - \sqrt {2gh} }}\) （3）

我们可以事先测量出m₁，用光电门传感器测出碰撞前m₁的速度，从高度计读出两者上升的高度h，得出上述数据后代入公式（3）就可以求出待测的质量m₁。

2．装置示意图

如图1所示：

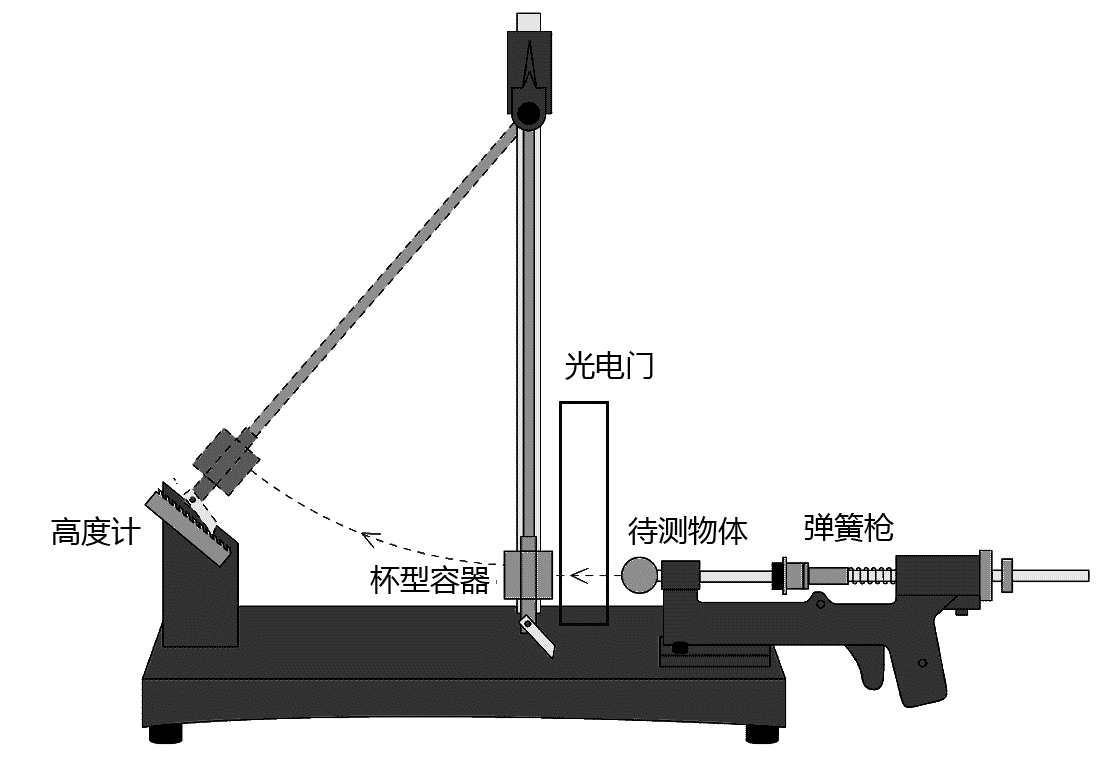
3．实验器材

铁架台、与轻直杆相连的杯形容器、弹簧枪、光电门传感器、高度计。

4．操作步骤

（1）测出待测物体的挡光宽度，光电门传感器需要这个值进一步测出碰撞前瞬间的瞬时速度；

（2）将待测物体放置于弹簧枪发射端后，使用弹簧枪将它射出；

（3）从高度计刻度上读出两者上摆的高度；

（4）代入公式（3）求出待测物体的质量。

发布时间：2014/1/2 下午9:44:40  阅读次数：5368